Министерство образования, науки и молодежи Республики Крым
Государственное бюджетное профессиональное образовательное учреждение
Республики Крым
«Симферопольский колледж радиоэлектроники»
УТВЕРЖДАЮ
Председатель Методического совета
___________________В.И.Полякова
«_____» _______________201__ г.
Методические указания
К практическим занятиям
по дисциплинеЕН.01. Математика
Специальности11.02.10 «Радиосвязь, радиовещание и телевидение»
г.Симферополь
201__ год
Методические указания составлены в соответствии с учебным планом и рабочей программой дисциплины «Математика» по специальности 11.02.10 «Радиосвязь, радиовещание и телевидение»
Обсуждено на заседании цикловой
методической комиссии № 2
«_____»________ 201__ г
Протокол № _________
Председатель ЦМК № 2
____________ А.В. Иванов
Разработчик _________ Л.А. Вихорь
_________ В.Ю. Новицкий
_________ И.И. Фролова
Содержание
1. Пояснительная записка. 5
Практическая работа №1 Тема: Решение систем линейных алгебраических уравнений. 7
Практическая работа №2 Тема: Нахождение производной функции. 13
Практическая работа №3 Тема: Исследование и построение графиков функций с помощью производной. 17
Практическая работа №4 Тема: Нахождение неопределенного интеграла. 21
Практическая работа №5 Тема: Решение задач на применение интегралов. 23
Практическая работа №6 Тема: Решение дифференциальных уравнений. 25
Практическая работа №7 Тема: Вычисление числовых характеристик дискретной случайной величины. 29
Практическая работа №8 Тема: Исследование рядов на сходимость. 33
Практическая работа №9 Тема: Разложение функций в ряд. 37
Практическая работа №10 Тема: Действия с приближенными величинами. 39
2. Критерии оценивания практических работ. 40
3. Учебно-методическое и информационное обеспечение. 42
Пояснительная записка
Методические указания к практическим работам по дисциплине «Математика» предназначены для студентов по специальности 11.02.10 Радиосвязь, радиовещание и телевидение.
Цель методических указаний: оказание помощи студентам в выполнении практических работ по дисциплине «Математика».
Настоящие методические указания содержат практические работы, которые позволят студентам закрепить теорию по наиболее сложным разделам дисциплины и направлены на формирование следующих компетенций:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
ПК 1.1. Разрабатывать схемы цифровых устройств на основе интегральных схем разной степени интеграции.
ПК 1.2. Выполнять требования технического задания на проектирование цифровых устройств.
ПК 1.4. Определять показатели надежности и качества проектируемых цифровых устройств.
ПК 2.3. Осуществлять установку и конфигурирование персональных компьютеров и подключение периферийных устройств.
ПК 3.3. Принимать участие в отладке и технических испытаниях компьютерных систем и комплексов; инсталляции, конфигурировании программного обеспечения.
В результате выполнения практических работ по дисциплине «Математика» студенты должны:
знать:
- применять методы дифференциального и интегрального исчисления;
- решать дифференциальные уравнения;
- исследовать ряды.
уметь:
- основные понятия и методы математического анализа, теории вероятности и математической статистики;
- основные методы дифференциального и интегрального исчисления;
- основные численные методы решения математических задач;
- основы теории рядов.
Описание каждой практической работы содержит: тему, цели работы, порядок выполнения работы, а так же перечень контрольных вопросов. Для получения дополнительной, более подробной информации по изучаемым вопросам, приведено учебно-методическое и информационное обеспечение.
Практическая работа №1
Тема:Решение систем линейных алгебраических уравнений.
Цель: Научиться выполнять действия над матрицами, вычислять определитель матрицы, находить обратную матрицу.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Матрицей размера m´n, где m- число строк, n- число столбцов,называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, аj- номер столбца.
А = 
Основные действия над матрицами.
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом,возможно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.

a (А+В) =aА ±aВ
А(a±b) = aА ±bА
Операция умножения матриц.
Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
A×B = C;
 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Определение. Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А =  ; В = АТ=
; В = АТ=  ;
;
другими словами, bji = aij.
Определитель матрицы.
Определение. Определителем матрицывторого порядка называется выражение
 .
.
Определение. Определитель матрицы третьего порядка можно найти по правилу Саррюса
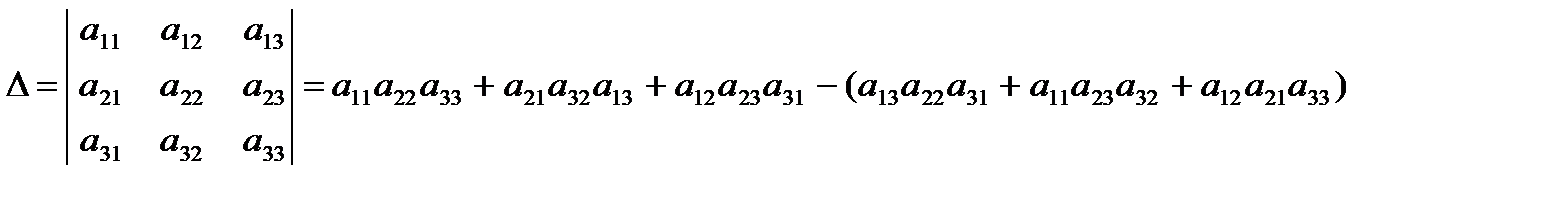 .
.
Для запоминания правила вычисления определителя третьего порядка предлагаем такую схему (правило треугольников):

Наметим точками элементы определителя, тогда слагаемыесо знаком «плюс» — этопроизведения элементов главной диагоналиa11, a22, a33ипроизведения элементов a13, a21, a32и a12, a23, a31, расположенныхв вершинах равнобедренныхтреугольников, основания которых параллельны главнойдиагонали. Со знаком «минус» берутся слагаемые, которые будут произведениями элементов второстепенной диагонали a13, a22, a31и в вершинах равнобедренных треугольников, основания которых параллельны второстепенной диагонали – a11, a23, a32и a12, a21, a33.
Миноры и алгебраические дополнения.
Определение. Пустьопределительимеет n строки n столбцов. Минором k-го порядка k  [1; n–1] называется определитель, образованныйиз элементов, расположенныхна пересечении каких-нибудьk строки k столбцовопределителя. Понятно, что минор первого порядка–этокакой-нибудьэлементопределителя.
[1; n–1] называется определитель, образованныйиз элементов, расположенныхна пересечении каких-нибудьk строки k столбцовопределителя. Понятно, что минор первого порядка–этокакой-нибудьэлементопределителя.
Определение. Дополнительным минором для минора k-го порядка называется такой минор, который остается вопределителе после вычеркивания тех k строки тех k столбцов, на пересечениикоторыхнаходятсяэлементыобразовавшие минор k-го порядка.
Определение. Алгебраическим дополнением к минору k-го порядка является дополнительный минор (n–k)-го порядка, взятый со знаком  , где
, где  .Если сумма
.Если сумма  номеров строки столбцов четное число, то берется знак «+», если нечетное– то знак «–».
номеров строки столбцов четное число, то берется знак «+», если нечетное– то знак «–».

Тут 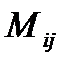 –дополнительный минор (n–1)-го порядка, образованный вычеркиванием i-строкии j-столбца в изначальномопределителе n-го порядка.
–дополнительный минор (n–1)-го порядка, образованный вычеркиванием i-строкии j-столбца в изначальномопределителе n-го порядка.
Теорема Лапласа (разложение определителя по строке или столбцу). Определителем n-го порядка называется число  , котороеравняется алгебраической суммепроизведений элементов какой-нибудьстрокиили столбца на соответствующиеему алгебраические дополнения:
, котороеравняется алгебраической суммепроизведений элементов какой-нибудьстрокиили столбца на соответствующиеему алгебраические дополнения:

или
 .
.
Алгебраические дополненияиз формулыдлявычисленияопределителя, являютсяв свою очередь, минорами, взятымиссоответствующими знаками, то естьопределителями (n–1)-го порядка. В итоге, вычислениеопределителя n-го порядкасводиться к вычислению n определителей (n–1)-го порядка.
По формуле вино, что при наличиивопределителе нулевых элементовсоответствующие алгебраические дополнения вычислять не нужно.
Метод Крамера.
Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.
Для этого необходимо, чтобы определитель матрицы системы не равнялся 0, т.е.detA¹ 0.
Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

, гдеD = detA, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца iстолбцом свободных членов bi.
Пример.

A =  ; D1=
; D1= 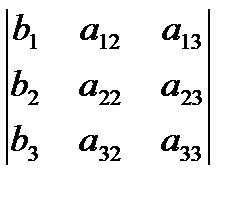 ; D2=
; D2=  ; D3=
; D3= 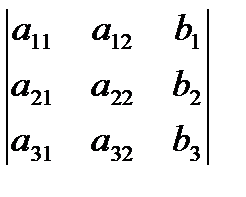 ;
;
x1 = D1/detA; x2 = D2/detA; x3 = D3/detA;
Метод Гаусса.
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a11¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
Получим:
 , где d1j = a1j/a11, j = 2, 3, …, n+1.
, где d1j = a1j/a11, j = 2, 3, …, n+1.
dij= aij – ai1d1j i = 2, 3, …, n; j = 2, 3, …, n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса.

Составим расширенную матрицу системы.
А* = 
Таким образом, исходная система может быть представлена в виде:
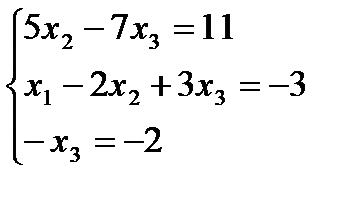 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Выполнить действия:
а)  ; б)
; б) 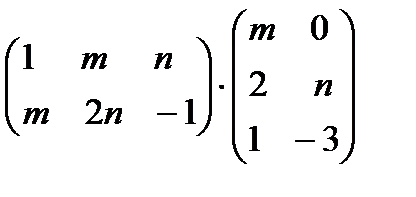 .
.
2. Вычислить определитель  двумя способами:
двумя способами:
а) по правилу Саррюса; б) по теореме Лапласа.
3. Решить систему уравнений тремя способами:
1) по формулам Крамера;
2) методом Гаусса;

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Основные сведения о матрицах. Действия над матрицами.
2. Определитель матрицы. Теорема Лапласа (о разложении определителя по элементам строки или столбца).
3. Алгебраические дополнения. Обратная матрица.
4. Формулы Крамера?
5. Метод Гаусса и Гаусса-Жордано?
6. Матричный метод решения СЛАУ?
7.
8.
Практическаяработа№2
Тема:Нахождение производной функции.
Цель: Научиться вычислятьпроизводные функций.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
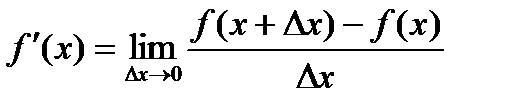
Основные правила дифференцирования.
Обозначим f(x) = u, g(x) = v - функции, дифференцируемые в точке х.
1) (C×u)¢ = C×(u)¢
2) (u±v)¢ = u¢±v¢
3) (u×v)¢ = u×v¢ + u¢×v
4)  , если v ¹ 0
, если v ¹ 0
5) (u(v))¢ = u¢(v)×v¢
Производные основных элементарных функций.
1) 
2) 
3) 
4) 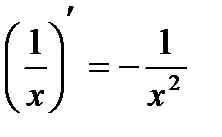
5) 
6) 
7) 
8) 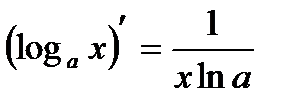
9) 
10) 
11) 
12) 
13) 
14) 
15) 
16) 
Производная сложной функции.
Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.Тогда

Производная показательно-степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu



Пример. Найти производную функции  .
.
Сначала преобразуем данную функцию: 

Пример. Найти производную функции  .
.

Пример. Найти производную функции 

ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Найти производные  функций:
функций:
1)  ;
;
2)  ;
;
3)  ;
;
2. Найти производную третьего порядка функции  .
.