Вернемся к рядам. В §2.7 мы установили, что если функцию 
можно разложить в сходящийся к ней степенной ряд, то он является для этой функции рядом Тейлора.
Возникает вопрос, справедливо ли обратное утверждение? Пусть функция бесконечно дифференцируема на интервале 
. Мы можем формально построить для нее ряд Тейлора. Но пока мы не знаем, будет ли наша функция суммой этого ряда, т.е. будет ли построенный ряд Тейлора сходиться к нашей функции на интервале , вместо знака равенства поставим знак соответствия:
Выясним, при каких условиях этот знак можно заменить на знак равенства. Напишем формулу Тейлора для функции :
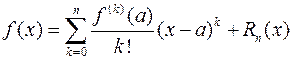, (2.9.1)
где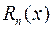 
- остаточный член, а
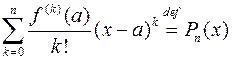. (2.9.2)
– многочлен Тейлора n -ой степени, который можно рассматривать как частичную сумму ряда Тейлора. Таким образом,
. (2.9.3)
Остаточный член формулы Тейлора для функции 
можно определить как разность между функцией и частичной суммой ряда Тейлора:
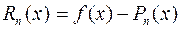. (2.9.4)
При увеличении номера п число слагаемых в частичной сумме, т.е. в многочлене Тейлора, увеличивается, а остаточный член изменяется. Можно рассмотреть последовательность остаточных членов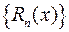 
. Это последовательность функций, определенных в той же окрестности точки а, в которой имеет место бесконечная дифференцируемость функции . Остаточный член показывает погрешность, получающуюся при замене функции частичной суммой ряда Тейлора. Ясно, что для получения хорошего приближения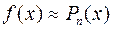 
последовательность остаточных членов 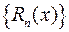должна стремиться к нулю. Вместо сочетания «последовательность остаточных членов» часто говорят просто «остаточный член».
Теорема 1 О необходимом и достаточном условии сходимости ряда Тейлора к функции .
Для того чтобы функцию можно было разложить в ряд Тейлора
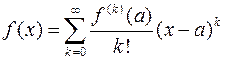(2.9.5)
на интервале , необходимо и достаточно, чтобы имела на этом интервале производные любого порядка и чтобы остаточный член 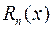в данной формуле Тейлора (2.9.1) стремился к нулю при всех 
, когда n ®¥.
Замечание. Если функция имеет на интервале производные любого порядка, то эти производные непрерывны на этом интервале, потому что, если имеет производную 
на , то производная 
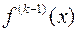должна быть непрерывна на этом интервале.
Доказательство. Необходимость. Дано: - сумма ряда (2.9.5), т.е. ряд сходится. Требуется доказать, что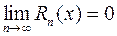 
. Воспользуемся равенством (2.9.3):
.
n -я частичная сумма ряда (2.9.4):
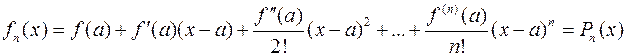
совпадает с многочленом Тейлора n -ой степени (2.9.2).
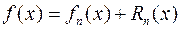(2.9.6)
Т.к. по условию ряд сходится,
.
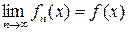Достаточность. Дано: 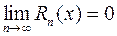. Требуется доказать, что - сумма ряда (2.9.5).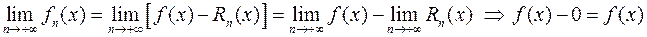 
.
Теорема доказана.
Лемма.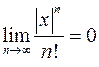 
(2.9.7)
для любого вещественного х.
В примере 3 на сходимость степенных рядов было установлено, что ряд 
сходится абсолютно при 
его радиус сходимости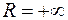 
. Отсюда следует, что общий член ряда 
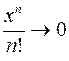при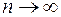 
(необходимое условие сходимости всякого ряда). Лемма доказана. Её можно применять и в виде 
.
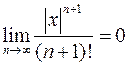Теорема 2 О достаточном условии сходимости остаточного члена формулы Тейлора к нулю.
Если функция в e-окрестности точки а имеет производные любого порядка, ограниченные одним и тем же числом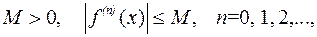 
то остаточный член ее формулы Тейлора в этой окрестности стремится к нулю при :
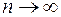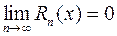. (2.9.8)
Доказательство. Воспользовавшись формулой остаточного члена (2.7.2):
, 
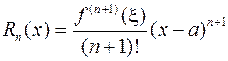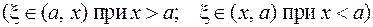
получим:
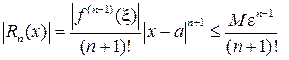, (2.9.9)
т.к.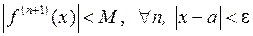 
в e-окрестности точки а.
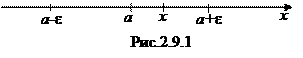Перейдем к пределу: 
.
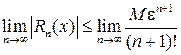По лемме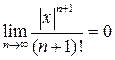 
при " х, в том числе при 
Þ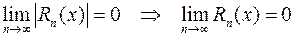 
. Теорема доказана.