Замечание. При использовании формул Виета нужно проверять существование корней.

Соотношения между корнями квадратного уравнения

 

Для решения следующих задач нам понадобятся формулы Виета. Эти формулы получаются из разложения квадратного трехчлена на сомножители: если — корни уравнения , то . Мы видим, что . Неплохо иметь в виду и формулы для квадратного уравнения общего вида : 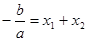, . Хотя можно обойтись и без них: нужно только не забыть поделить все члены уравнения на коэффициент . Итак, формулы Виета выражают сумму и произведение корней через коэффициенты уравнения.

Выразим через коэффициенты уравнения сумму квадратов корней уравнения: . Напомним, что это формула для приведенного уравнения. Обратите внимание: если дискриминант уравнения равен нулю, то считают, что уравнение имеет два равных корня (а не один), т. е. и .

Выразим через коэффициенты уравнения сумму кубов корней уравнения: = .

Аналогично выразим сумму четвертых степеней корней уравнения = .

Замечание. При использовании формул Виета нужно проверять существование корней.

Рассмотрим несколько задач на применение полученных формул:

1. Вычислить , где — корни уравнения . Решение. Преобразуем данное выражение = . Из приведенного уравнения получаем . Вычисляя полученное выражение, находим . Проверим, что корни существуют: 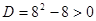. Ответ: 464.

2. Вычислить значение выражения , где — корни уравнения , и выяснить, какое число больше, или 1,999? Решение. По формулам Виета . (Так как в данном случае , то и корни существуют). Ответ: .

3. Вычислить значение выражения , где — меньший, а – больший корни уравнения . Решение. Вычислим значение . Отсюда . Ответ: .

3. Найти квадратное уравнение с корнями , где являются корнями уравнения . Решение. Очевидно, уравнение имеет корни. Пусть — искомое уравнение. Тогда , , значит, = . Итак, . Итак, искомое уравнение имеет вид . Ответ: .

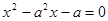4. При каких корни уравнения на единицу больше корней уравнения ? Решение. Пусть – корни уравнения , тогда по формулам Виета . При этом для первого уравнения , или , . Отсюда получаем , . Второе уравнение является тождеством, решая первое, получаем . Проверкой устанавливаем, что и в том, и в другом случае корни существуют. Ответ: .

Продолжение этой темы — задача такого типа: имеется квадратное уравнение с параметром, нужно найти значение параметра, при котором некоторое выражение, составленное из корней уравнения, имеет определенное значение.

 

5. При каких значениях сумма квадратов корней уравнения 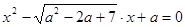равна 4? Решение. Используя формулу для суммы квадратов корней, получаем уравнение , . Поскольку сами корни при этом не находились, надо обязательно проверить их существование. Подставим полученные значения в уравнение и получим два уравнения: при , при . Найдем дискриминанты этих уравнений. Мы видим, что при , а при 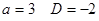, значит, корней не существует. Ответ: .

6. Найти все значения , при которых корни уравнения удовлетворяют условию 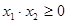. Решение. Сначала определим, для каких значений параметра данное уравнение имеет действительные корни. Для этого найдем дискриминант и потребуем, чтобы он был неотрицательный: . Так как , то получаем неравенство . Находим общую часть (пересечение) полученных множеств: . Ответ: .

7. Найти все значения , при которых корни уравнения удовлетворяют условию 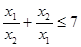. Решение. Сначала определим, для каких значений параметра данное уравнение имеет действительные корни. Для этого найдем дискриминант и потребуем, чтобы он был неотрицательный: . Чтобы решить это неравенство, поищем корни соответствующего уравнения: . Но оно не имеет действительных корней, значит, неравенство выполняется для любых значений . Итак, данное уравнение имеет корни при любых . Теперь займемся самим условием. Выразим через коэффициенты данное выражение: . Получаем неравенство . Решаем неравенство методом интервалов: находим нули числителя и знаменателя и отмечаем на числовой прямой (рис. 1). Ответ: .

Дальнейшее развитие этой темы представляет собой следующая задача.

8. При каких значениях сумма квадратов корней уравнения является наименьшей? Чему равна эта сумма? Решение. Выясним сначала, при каких значениях корни существуют: . Решая это неравенство, получаем . Затем, используя формулу для суммы квадратов корней, получаем = 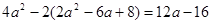, где . Полученное выражение на промежутке принимает наименьшее значение в точке 2, это значение равно 8. Ответ:

9. При каких значениях сумма квадратов корней уравнения является наименьшей? Чему равна эта сумма? Решение. Выясним сначала, при каких значениях параметра корни существуют: 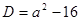. Решая это неравенство, получаем . Затем, используя формулу для суммы квадратов корней, получаем , где 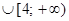. Полученное выражение на множестве . принимает наименьшее значение в точках –4 и 4, это значение равно 8. Ответ: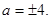

 

В следующих задачах используется такое соотношение между корнями, которое непосредственно не выражается через коэффициенты. В этом случае составляем систему, где два уравнения — формулы Виета, а третье — заданное соотношение. При решении такой системы корни уравнения обычно находятся, поэтому специально проверять их существование не надо.

10. При каких значениях разность корней уравнения равна 14? Решение. Пусть — корни уравнения. Составляем систему . Складывая первое и третье уравнение, получаем , отсюда и 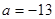. Ответ: –13.

11. При каких значениях один из корней уравнения 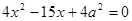равен квадрату другого? Решение. Пусть — корни уравнения. Составляем систему . Подставляя в первое уравнение, получаем , 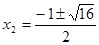. Пусть , тогда и , а это невозможно. Пусть , тогда и , отсюда . Ответ: .

12. Найти и 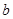, если уравнение имеет два корня, разность которых равна 3, причем модуль меньшего корня в два раза больше модуля большего корня. Решение. Пусть — корни уравнения, причем 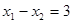. Отсюда следует, что является большим корнем, поэтому . Получаем систему . Решая уравнение , получаем два решения: . По формулам Виета , , отсюда находим два значения: и . Ответ: и .

Хотя большинство задач подобного содержания решается с помощью формул Виета, как всегда, имеются исключения. Попадаются задачи, где самый рациональный путь — найти корни и потребовать выполнения условий задачи.

13. При каких абсолютная величина разности между различными корнями уравнения меньше 4? Решение. В данном случае проще всего найти корни и составить нужное неравенство: , . Решаем неравенство . Изобразим решения этих неравенств на двух числовых прямых (рис. 2):

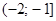
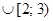Получим промежутки . Исключим точки –1 и 2, поскольку при таких получаются равные корни. Ответ: .

14. Известно, что корни уравнения на 1 меньше корней уравнения . Найти значение параметра и корни. Решение. Пусть — корни первого уравнения, тогда — корни второго уравнения. Составим систему из формул Виета: 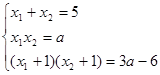. Вычитая из третьего уравнения второе, получаем , отсюда . Решая уравнение , получаем корни 2 и 3. Ответ: .

15. При каких значениях разность корней уравнения равна 5, а разность их кубов равна 35? Решение. Пусть — корни уравнения. Составим систему из данных условий: . Поделив второе уравнение на первое, получим уравнение 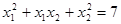. Подставив в него , получим , или . Корни этого уравнения –2 и –3. При получаем отсюда . При получаем отсюда . Ответ: .