Сравнение метода установления и метода Якоби

Постановка задачи

Уравнение:

1;

Граничные условия:

u (0 ,y) = X 0(y);	u (1 ,y) = X 1(y);
u (x, 0) = Y 0(x);	u (x, 1) = Y 1(x);

Для данного варианта:

);

Аналитическое решение

Делаем подстановку W = u ² / 2 и ищем решение в виде

Находим C = 1 / 2 и получаем решение, удовлетворяющее заданным начальным условиям:

Построим его график:

1 h = 0.2; %step 2 % domain 3 x0 = 0; 4 xf = 1; 5 y0 = 0; 6 yf = 1; 7 %grid 8 x = x0:h: xf; 9 y = y0:h: yf; 10 N = size (x,2); 11 U_theory = zeros (N,N); 12 for n = 1:N 13 for m = 1:N 14 U_theory(m,n) = sqrt (sin (pi*h*(n-1))*(sin (pi*h*(m-1)/3) 15 +cos (pi*h*(m-1)/3))); 16 end; 17 end; 18 mesh(y,x, U_theory);

Рис. 1: Аналитическое решение ДУ

Истинные значения функции на узлах сетки:

U_theory =	0.7667	0.9752	0.9752	0.7667	0.0000
	0.8350	1.0621	1.0621	0.8350	0.0000
	0.8809	1.1206	1.1206	0.8809	0.0000
	0.9061	1.1526	1.1526	0.9061	0.0000
	0.9111	1.1589	1.1589	0.9111	0.0000
	0.8961	1.1398	1.1398	0.8961	0.0000

Численные решения

Разностная схема

Аппроксимируем по схеме "крест". Количество узлов , где h - шаг сетки (одинаковый по x и y).

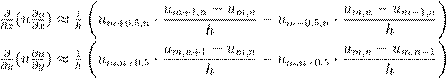
Для точек в середине узлов воспользуемся средним значением: и т.д. В итоге получим:

А для f(x, y):

Итоговая разностная задача:

Метод установления для уравнения параболического типа

Метод установления заключается в численном решении нестационарной задачи, которая на больших временах сходится к исходной стационарной.

Добавив производную по времени и аппроксимируя её как , получим выражение для значения :

Для начала определим минимальное количество итераций S, необходимых для сходимости решения с точностью , а так же оптимальный временной шаг τ_opt.

Выбрав шаг сетки h_x = h_y = h = 0.2, вычислим собственные значения оператора Лапласа λmin,λmax:

Тогда

, где Соответствующий код:

% S and tau search % S - number of iterations % tau - step eps = 0.01; lambda_min = 2*pi ^2/(xf -x0) lambda_max = 8/h^2 - lambda_min tau_max = 2/lambda_max tau_opt = 2/(lambda_max+lambda_min) xi = lambda_min/lambda_max; rho = (1 - xi)/(1+ xi); S = log (eps)/ log (rho); S = ceil (S)

В итоге получаем:

lambda_min = 19.7392 lambda_max =180.2608 tau_max = 0.0111 tau_opt = 0.0100

S = 21

Расчет значений функции f (x,y) в узлах сетки:

%let 's find f (m,n): for n = 1:N for m = 1:N f (m,n) = -5* pi^2/9*sin (pi*h*(n-1))*(sin (pi*h*(m-1)/3) +cos (pi*h*(m-1)/3)); end; end;

Методом простых итераций находим значения функции в узлах сетки:

%now let 's find U(m,n): U = zeros (N,N); U(:,1) = 0; U(:,N) = 0; U(1,:) = (sin (pi*y)).^0.5; U(N,:) = ((1+ sqrt (3))/2* sin (pi*y)).^0.5; for s = 1:S for n = 2:(N-1) for m = 2:(N-1) U0 = U; U(m,n) = U0(m,n) + (tau_opt/2/h^2)*(U0(m+1,n)^2+U0(m-1,n)^2+ +U0(m,n+1)^2+U0(m,n-1)^2 -4*U0(m,n)^2) - tau_opt*f (m,n); end; end; end; mesh(y,x,U)

Рис. 2: Решение методом установления

U =	0.7667	0.9752	0.9752	0.7667	0.0000
	0.8393	1.0684	1.0687	0.8402
	0.8875	1.1298	1.1301	0.8885
	0.9132	1.1622	1.1625	0.9139
	0.9165	1.1661	1.1662	0.9168
	0.8961	1.1398	1.1398	0.8961	0.0000

Учитывая полученное аналитическое решение, находим получившуюся точность метода:

eps_fact = max(max(abs(U-U_theory)))

eps_fact = 0.0099

Метод Якоби

Вернемся к исходной разностной схеме. В методе Якоби на каждом шаге в каждом внутреннем узле решение пересчитывается по значениям соседей на предыдущем шаге. Заменим в исходной разностной задаче , оставив у остальных слагаемых порядок итерации s, например, : Тогда, выразим :

Количество итераций определяется по тем же формулам, что и в случае метода установления. Шаг сетки h оставим тем же.

U = zeros (N,N); U(:,1) = 0; U(:,N) = 0; U(1,:) = (sin (pi*y)).^0.5; U(N,:) = ((1+ sqrt (3))/2* sin (pi*y)).^0.5; for s = 1:S for n = 2:(N-1) for m = 2:(N-1) U0 = U; U(m,n) = 1/4*(U0(m+1,n)^2+U0(m-1,n)^2+U0(m,n+1)^2+U0(m,n-1)^2) - h^2*f (m,n)/2; U(m,n) = sqrt (U(m,n)); end; end; end; mesh(y,x,U)

Рис. 3: Решение методом Якоби

U =	0.7667	0.9752	0.9752	0.7667	0.0000
	0.8408	1.0696	1.0696	0.8409
	0.8892	1.1311	1.1311	0.8893
	0.9144	1.1632	1.1632	0.9145
	0.9170	1.1665	1.1665	0.9171
	0.8961	1.1398	1.1398	0.8961	0.0000

Точность метода:

eps_fact = 0.0106

Сравнение метода установления и метода Якоби

Сравним евклидовы нормы разностей решений метода установления с аналитическим || MSJ_n || и аналитического решения с методом Якоби || J_n ||:

err = norm(U-U_theory)

err_ustanovlenia = 0.0295 err_jacobi = 0.0331

То есть метод установления приближает данную задачу точнее.

Вывод:

В данном случае метод установления сходится лучше, точность получается лучше заданного, в то время как у методы Якоби погрешность в отдельных точках совсем немного, но превышает. На практике это не должно играть роли.

Список литературы:

1) Е.Н. Аристова, А. И. Лобанов – «Практические занятия по вычислительной математике в МФТИ»

2) pyrkovaoa-fizteh.ru