Множества. Операции над множествами
Понятие множества является ключевым в математике, без которого невозможно изложение ни одного из ее разделов.
Множество – первичное понятие математики, т.е. это понятие не определяется через другие, а только поясняется. Создатель теории множеств Г. Кантор (1845-1918) определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью», а также «множество есть многое, мыслимое нами как единое». Разумеется, эти слова не могут рассматриваться как математически строгое определение множества.
Множество – это совокупность каких-либо объектов. Так, можно говорить о множестве целых чисел, о множестве точек на прямой, о множестве жителей города и т.д. Объекты, входящие в данное множество, называются элементами множества. Элементами множеств могут быть самые разнообразные предметы: буквы, числа, функции, точки, углы, люди и т.д.
Множества, состоящие из конечного числа элементов, называются конечными, а множества, состоящие из бесконечного числа элементов, – бесконечными.
Множества обычно обозначаются большими буквами А, В, X, а их элементы малыми а, b, х.
Запись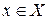 
означает, что объект х есть элемент множества X. Если х не принадлежит множеству X, то пишут 
.
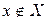Запись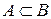 
(множество А содержится в В) означает, что каждый элемент множества А принадлежит В. В этом случае множество А называют подмножеством множества В.
Множества А и В называют равными (
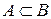), если и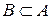 
.
Пример 2.1.1. Множества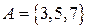 
и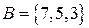 
равны, т.к. состоят из одинаковых элементов.
Если множество не содержит ни одного элемента, то его называют пустым и обозначают символом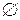 
.
Множество задают либо перечислением его элементов, либо описанием свойств множества, которые четко определяют совокупность его элементов. При втором способе множество обычно определяется как совокупность тех и только тех элементов из некоторого основного множества T, которые обладают свойством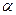 
. В этом случае используют обозначение 
.
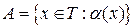Пример 2.1.2. Множество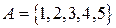 
равно множеству 
, где N – множество натуральных чисел.
Множества можно определять также при помощи операций над некоторыми другими множествами. Пусть имеются два множества А и В.
Объединение (сумма) 
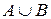есть множество всех элементов, принадлежащих А или В, т.е. 
.
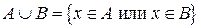Пример 2.1.3.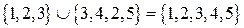 
.
Пересечение (произведение)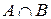 
есть множество всех элементов, принадлежащих как А, так и В, т.е. 
.
Пример 2.1.4.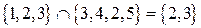 
.
Множества, не имеющие общих элементов (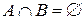
), называют непересекающимися.
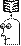Разность 
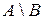есть множество, состоящее из всех элементов А, не входящих в В, т.е. 
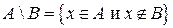. Ее можно рассматривать как относительное дополнение В до А.
Пример 2.1.5.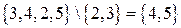 
.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ
К Лене на день рождения пришли гости с подарками. Получилось так, что дарили только букеты цветов и воздушные шарики. Шесть гостей подарили букеты цветов, четыре – воздушные шарики. Сколько было гостей?
Ответ: количество гостей 6-10.
Из 25 студентов группы 20 человек увлекаются спортом, 9 – музыкой, 6 – музыкой и спортом. Сколько студентов увлекается только спортом, сколько – только музыкой, а сколько – ничем не занимаются?
Ответ: 14, 3 и 2 студентов соответственно.
Миша, Коля, Лева вместе прочитали 3 книги. Миша и Коля вместе прочитали 5 книг; Миша и Лева вместе – 4 книги; Коля и Лева вместе – 3 книги. Миша прочитал 8 книг; Коля – 6 книг; Лева – 5 книг. Сколько книг прочитали дети?
Ответ: 10 книг.
Из 110 студентов английский язык изучают 44 человека, немецкий – 50 человек, французский – 49 человек, английский и немецкий – 13, английский и французский – 14, немецкий и французский – 12, все три языка изучают 5 человек. Сколько студентов изучают только один язык? Сколько студентов не изучают ни одного языка?
Ответ: 80 и 1.
При школе был приусадебный участок с теплицей. В субботу группа ребят работала на этом участке. Они ремонтировали теплицу, поливали огурцы, помидоры и капусту. По окончании работы потребовались сведения о числе работавших, но мнения ребят разошлись, и узнать ничего не удалось.
Было установлено только следующее, Ребята, ремонтировавшие теплицу, не занимались поливкой, а ребята, поливавшие овощи, не участвовали в ремонте теплицы. Никто из ребят не поливал одновременно огурцы и капусту. Некоторые ребята поливали помидоры и огурцы, некоторые поливали помидоры и капусту, но не было таких ребят, которые поливали бы только помидоры. Огурцы поливало 7 человек, а помидоры – 4. Число ребят, ремонтировавших теплицу, было на 2 меньше числа ребят, поливавших только огурцы. Удвоенное число ребят, поливавших только капусту, было на 1 больше утроенного числа тех ребят, которые поливали только огурцы.
Этих сведении оказалось достаточно, чтобы установить число работавших. Сколько же ребят было в субботу на приусадебном участке?
Ответ: 20 ребят.
Алгебра логики
Таблицы истинности для основных операций алгебры высказываний
Таблица
| Первое высказывание | Второе высказывание | Отрицание первого высказывания | Конъюнкция | Дизъюнкция | Импликация | Эквивалентность |
| А | В | 
| 
| 
| 
| 
|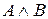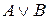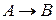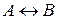