Примеры:
ввода матриц, строки, столбца, квадратной матрицы, транспонирования матриц:
>> A=[21 34 57]
A =
21 34 57
>> a=A';
>> a=[21 34 57]'
a =
>> B=[21 34 57; 98 59 46; 67 90 34]
B =
21 34 57
98 59 46
67 90 34
>> b=B';
>> b=[21 34 57; 98 59 46; 67 90 34]'
b =
21 98 67
34 59 90
57 46 34
Вычисление определителя
>> det(B)
ans =
Обращение матрицы, естественно, квадратной:
>> d=B^(-1);
>> d=[21 34 57; 98 59 46; 67 90 34]^(-1)
d =
-0.0095 0.0177 -0.0080
-0.0011 -0.0139 0.0206
0.0217 0.0017 -0.0093
С использованием приведенных матриц определим решение линейного матричного уравнения B*X = a как X=B^(-1)*a = d*a:
>> X=d*a
X =
-0.0546
0.6806
-0.0174
Отметим, что наряду с операциями линейной алгебры, над матрицами производятся поэлементные операции, т.е. действия с элементами различных матриц, имеющих одинаковые номера.
Для матриц a и b, где (вместо пробелов применимы запятые)
>> a=[1,3,5;0,9,7;6,2,2])
a =
1 3 5
0 9 7
6 2 2,
>> b=[7,8,4;4,9,3;1,3,2]
b =
7 8 4
4 9 3
1 3 2,
матричное произведение
>> a*b
ans =
24 50 23
43 102 41
52 72 34.
Поэлементное произведение, команда на вычисление которого отмечена точкой перед звездочкой,
>> a.*b
ans =
7 24 20
0 81 21
6 6 4.
Обратите внимание на то, что матричное и поэлементное произведения матриц – это совершенно различные матрицы.
Некоторые другие примеры поэлементных операций над матрицами одной и той жеразмерности:
>> [1 3 2].*[7 5 4]
ans =
7 15 8.
>> [1 3 2]./[7 5 4]
ans =
0.1429 0.6000 0.5000.
>> [1 3 2].\[7 5 4]
ans =
7.0000 1.6667 2.0000.
>> [1 3 2].^[7 5 4]
ans =
1 243 16
Интересной матрицей, рассматриваемой в МАТЛАБ-е, является магический квадрат, суммы членов которого, на всех диагоналях, во всех строках и всех столбцах, одинаковы. Его примеры:
>> magic(3)
ans =
8 1 6
3 5 7
4 9 2,
>> magic(4)
ans =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1.
- Функции и графики.
Рассматривается:
- ввод аргументов для расчета функций,
- расчет элементарных функций и их комбинаций вида функций от функций,
- построение двумерных и трехмерных графиков функций с использованием различных
технологий и изобразительных средств, предоставляемых МАТЛАБ пользователю.
Сначала рассмотрим функции одного аргумента x.
Используем двоеточие – знак перечисления и зададим значения аргумента на выбранном промежутке с выбранным шагом.
Подавим печать матрицы значений, поставив в конце команды точку с запятой.
Если не указать шаг вычислений, то по умолчанию он будет выбран единичным.
Если не подавить печать значений аргумента, то на экране монитора появится длинная матрица этих значений.
Для построения графика используем команду plot.
Приведем и обсудим пример – построение синусоиды на 0 ≤ x ≤ 10.
>> x=0:10
x =
0 1 2 3 4 5 6 7 8 9 10
>> plot(x,sin(x))
В окне, вызываемом в меню Window командой Fig.1, получим график:
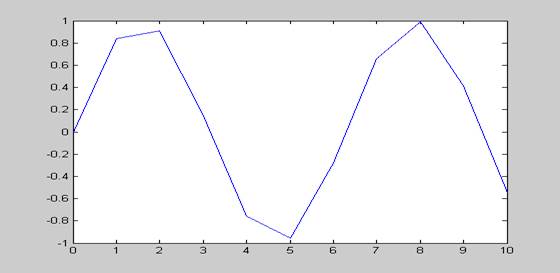
Сгенерировали сначала совершенно не нужную нам последовательность целых чисел от 0 до 10, затем кусочно-ломаную кривую, отдаленно напоминающую синусоиду.
Исправим ошибки.
Единичный шаг вычислений заменим достаточно малым, выберем 0.01, печать получающейся при этом матрицы-строки из 10001 элемента подавим точкой с запятой.
Командой grid нанесем на график сетку.
Войдя в меню Insert, получим возможность озаглавить график и сделать надписи
на осях. Получим аккуратную синусоиду.
x=0:.01:10;
plot(x,sin(x)),grid

Построим синусоиду в полярных координатах, используя команду polar:
>> x=0:.01*pi:2*pi;
>> polar(x,sin(x))

Построим на одном и том же графике пару кривых, например, синусоиду и косинусоиду для двух их периодов.
>> x=-2*pi:.01*pi:2*pi;
>> y=sin(x);
>> z=cos(x);
>> plot(x,sin(x),x,cos(x)),grid

Теперь построим для промежутка 2pi два семейства из пяти синусоид каждое, различающихся в первом случае амплитудой, во втором – частотой.
Для этого в команды встроим матрицы – столбцы (транспонированные матрицы -строки) множителей, в первом случае – амплитуд, во втором – частот.
x=0:.01*pi:2*pi;
>> y=[1:5]'*sin(x);
>> plot(x,y),grid

>> x=0:.01*pi:2*pi;
>> y=sin([1:5]'*x);
>> plot(x,y),grid

Номера кривых на графиках соответствуют номерам цветов радуги в обычном перечне: 1 – красный, 2 – оранжевый и т.д.
Обратим внимание на возможность рассчитывать и отображать на графиках сложныефункции вида функций от комбинаций элементарных функций.
Пример: - log2|cos(x^2)|:
x=.4:.01:2.5;
>> y=-log2(abs(cos(x.^2)));
>> plot(x,y),grid

Построение графика сложной функции в полярных координатах:
>> x=0:.01*pi:2*pi;
>> polar(x,abs(sin(3*x)))

Пока мы имели дело с двумерными графиками.
Теперь построим трехмерную спираль, используя команду построения трехмерных графиков plot3.
>>x=-pi:.01*pi:2*pi;
>>y=sin(x);
>>z=cos(x);
>>plot3(x,y,z),grid

Многие другие графические средства, одно- и многооконные, двумерные и трехмерные вы можете освоить с помощью графического раздела справочного аппарата системы.
Введенные значения аргумента x и функций от него составляют матрицы-строки, арифметические операции над такими матрицами выполняются поэлементно, что возможнолишь при одинаковой длине матриц, и отмечаются точкой перед символом операции.
- Выполнение операций математического анализа с использованием пакета символьной математики.
На примерах рассмотрим технику использования пакета символьной математики для: - дифференцирования,
- интегрирования функций одной переменной,
- решения алгебраических уравнений
- интегрирования дифференциальных уравнений.
Для обращения к пакету указывается принадлежность переменных к символьным записью вида x=sym(‘x’); y=sym(‘y’) или syms x y или выделением выражений апострофами.
Определение n-ной производной по x от выражения F(x) выполняется по команде формата diff(‘F(x)’,’x’,n) или diff(F(x),x,n), если ранее указано, что x – символьная переменная, указывается лишь n > 1.
Примеры:
>> diff('exp(x)*cos(x)','x',2)
ans =
-2*exp(x)*sin(x).
>> syms x a
>> diff(sin(a*x)/x,x)
ans =
cos(a*x)*a/x-sin(a*x)/x^2.
Команда на вычисление неопределенного интеграла – int('F(x)’,'x').
Пример:
>> int('exp(x)*cos(x)','x')
ans =
1/2*exp(x)*cos(x)+1/2*exp(x)*sin(x).
Команда на вычисление определенного интеграла содержит, кроме того, пределыинтегрирования.
Примеры:
>> int('exp(x)*cos(x)','x',0,2)
ans =
1/2*exp(2)*cos(2)+1/2*exp(2)*sin(2)-1/2.
>> int('exp(x)*cos(x)','x',0,pi*3/2)
ans =
-1/2*exp(3/2*pi)-1/2.
Вычисления можно довести до приближенного ответа:
Пример.
>> -1/2*exp(3/2*pi)-1/2
ans =
-56.1589.
Вычисление кратных интегралов выполняется по схеме «интеграл от интеграла отинтеграла…».
Алгебраические выражения, в том числе получаемые при интегрировании, можноупрощать, правда, во многих случаях слабее, чем это делают абитуриенты МАИ, командой формата simple(F(x)).
Например, выполнение команды simple(1/2*exp(x)*cos(x)+1/2*exp(x)*sin(x)) состояло в переборе многих вариантов и привело к скромному результату:
ans =1/2*exp(x)*(cos(x)+sin(x)).
Решение алгебраических уравнений вида F(x) = 0 выполняется по команде формата solve(‘F(x)’).
Примеры.
>> solve('x^2-2')
ans =
[ 2^(1/2)]
[ -2^(1/2)].
Ответ простой, обозримый.
Но вот другой случай:
>> solve('x^3-2*x^2+x-5')
ans =
[1/6*(532+12*1965^(1/2))^(1/3)+2/3/(532+12*1965^(1/2))^(1/3)+2/3]
[ -1/12*(532+12*1965^(1/2))^(1/3)-1/3/(532+12*1965^(1/2))^(1/3)+2/3+1/2*i*3^(1/2)*(1/6*(532+12*1965^(1/2))^(1/3)-2/3/(532+12*1965^(1/2))^(1/3))]
[ -1/12*(532+12*1965^(1/2))^(1/3)-1/3/(532+12*1965^(1/2))^(1/3)+2/3-1/2*i*3^(1/2)*(1/6*(532+12*1965^(1/2))^(1/3)-2/3/(532+12*1965^(1/2))^(1/3))]
Полученные точные значения корней вычисляются приближенно после перемещения их мышкой к курсору:
>> [ 1/6*(532+12*1965^(1/2))^(1/3)+2/3/(532+12*1965^(1/2))^(1/3)+2/3]
ans =
2.4334,
>> [
-1/12*(532+12*1965^(1/2))^(1/3)-1/3/(532+12*1965^(1/2))^(1/3)+2/3+1/2*i*3^(1/2)*(1/6*(532+12*1965^(1/2))^(1/3)-2/3/(532+12*1965^(1/2))^(1/3))]
ans =
-0.2167 + 1.4170i,
>> [
-1/12*(532+12*1965^(1/2))^(1/3)-1/3/(532+12*1965^(1/2))^(1/3)+2/3-1/2*i*3^(1/2)*(1/6*(532+12*1965^(1/2))^(1/3)-2/3/(532+12*1965^(1/2))^(1/3))]
ans =
-0.2167 - 1.4170i.
Аналогично решаются системы алгебраических уравнений.
Например, система уравнений P(x,y,z)=0, Q(x,y,z)=0, R(x,y,z)=0 решается по команде формата:
[x,y,z]=solve(‘P(x,y,z)’, ‘Q(x,y,z)’, ‘R(x,y,z)’,’x’,’y’,’z’).
В качестве упражнения введите команду
>> [x,y,z]=solve('x^2+y^3+z^4-10','x+2*y-3','z-5*x+4','x','y','z')
а затем полученные точные решения системы уравнений пересчитайте в приближенные, но обозримые.
Интегрирование дифференциальных уравнений и их систем выполняется
функцией dsolve.
Проинтегрируем некоторые простейшие дифференциальные уравнения.
Здесь аргумент – t, dx/dt=Dx, в случае отсутствия начальных условий решение получается в общем виде, с неопределенными множителями, при указании достаточного количества начальных условий решение получается численным и при желании исполнителя может быть отображено графически.
Примеры.
>> dsolve('Dx=-x')
ans =
C1*exp(-t).
>> dsolve('Dx=-x','x(0)=1')
ans =
exp(-t).
>> dsolve('Dx=-x^2','x(0)=1')
ans =
1/(t+1)
>> t=0:.05:10;
>> plot(t,exp(-t),t,1./(t+1)),grid

- Численное интегрирование обыкновенных дифференциальных уравнений
Методом Рунге-Кута.
Такое интегрирование традиционно для МАТЛАБА, оно требует:
- сначала создать файл-функцию, содержащий правую часть дифференциального
уравнения, записанного в нормальной форме и начинающийся со слова function,
- затем создать файл-сценарий с указанием подынтегральной функции, интервала
интегрирования и начальных условий.
Кратко обозначив используемые здесь файлы как студенческие функцию и интеграл, приведем их, команду на интегрирование и результат его:
%studf
function xprime=studf(t,x);
xprime=-1.5*x;
%studint
[t,x]=ode45('studf',[0 5],[1]);
plot(t,x),grid
>> student.
Результат представлен на графике ниже.

Очевидно, здесь при единичном начальном условии было проинтегрировано дифференциальное уравнение dx/dt=-1.5*x, и получена экспонента.
Литература (основная):
1. Дьяконов В.П. MATLAB 6/6.1/6.5+SIMULINK. Основы применения.
Полное руководство пользователя. Москва: Солон-Пресс, 2002.