Силы, действующие в механизмах

СИЛОВОЙ АНАЛИЗ МЕХАНИЗМОВ

3.1. Общие сведения и определения. Силы, действующие в механизмах

При проведении силового анализа решаются следующие основные задачи:

1. Определение реакций в кинематических парах механизмов, находящихся под действием заданных внешних сил. Эти реакции затем используются для расчёта звеньев и элементов кинематических пар (подшипников, например) на прочность, жёсткость, долговечность и т.д.

2. Определение уравновешивающей силы 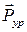или уравновешивающего момента , приложенных к ведущему звену. Они уравновешивают внешние силы, приложенные к механизму. Эти величины нужны, например, для выбора двигателя, приводящего в движение данный механизм.

 

Силы, действующие в механизмах

Различают две большие группы сил:

движущие силы Р_дв. или моменты движущих сил М_дв., которые:

– совершают положительную работу;

– направлены в сторону скорости точки приложения силы или под острым углом к ней;

– задаются посредством механической характеристики двигателя;

силы сопротивления Р _С и их моменты М _С, которые

– совершают отрицательную работу;

– направлены противоположно скорости.

Они подразделяются на силы:

– полезного сопротивления Р _п.с. и моменты М _п.с.;

– вредного сопротивления:

а) трения в кинематических парах,

б) сопротивления среды,

в) внутреннего сопротивления (например, силы упругости звеньев).

Кроме того, существуют:

– силы веса , где r - плотность материала, V – объём звена детали;

– силы инерции ,

– моменты сил инерции , где

m_u, J_S – масса и массовый момент инерции звена; и - линейное и угловое ускорения;

– силы реакций в кинематических парах .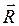

 

Силы инерции звеньев и моменты сил инерции.

Из теоретической механики известно, что все силы инерции звена, совершающего плоскопараллель­ное движение и имеющего плоскость симметрии, па­раллельную плоскости движения, могут быть сведены:

– к силе инерции , приложенной в центре масс S звена;

– к паре сил инерции, момент которых обозначим .

– главный вектор сил инерции, который в дальнейшем будем называть силой инерции;

– главный момент сил инерции, который в дальнейшем будем называть моментом сил инерции, где m – масса звена, J_S – массовый момент инерции относительно центра масс, – ускорение центра масс, – угловое ускорение звена.

и направлены в стороны, противоположные ускорениям и .

Удобно для дальнейших расчётов заменить и одной силой. Для этого можно использовать 3 метода:

а) Метод замещающих точек: (см. /3/, стр. 252).

б) Перенос силы на плечо . При этом момент сил инерции заменяется парой сил с плечом h_u (рис. 3.1), причём одна из этой пары сил приложена к центру масс звена S и направлена противоположно преобразуемой силе , а другая сила смещена на плечо h_u и приложена к точке К. Здесь К – центр качания звена.

 

 

Рис. 3.1. Перенос силы на плечо при замене силы и момента одной силой

в) Определение центра качания звена через мгновенный центр ускорений (МЦУ).

При этом сила инерции переносится па­раллельно самой себе на расстояние (рис. 3.2), вычис­ленное по формуле

, мм.

Здесь – мгновенный центр ускорений звена, откладывается в сторону, являющуюся продолжением отрезка

Рис. 3.2. Определение центра качания звена

 

3.2. Статическая определимость кинематической цепи

При силовом анализе механизмов (определении неизвестных сил, действующих на движущиеся звенья) можно использовать уравнения (законы) статики. Это положение докажем ниже:

Проанализируем реакции в кинематических парах:

 

Кинематические пары 5-го класса	Равновесие каждого звена	Известные параметры	Неизвестные параметры
вращательная		Точка приложения	Величина, направление
поступательная		Направление	Величина, точка приложения
Кинематические пары 4-го класса		Точка приложения, направление	Величина

Из приведенной таблицы следует, что в кинематических парах 5 класса известно по одному параметру сил реакций, неизвестны два. В кинематических же парах 4 класса известны два параметра, а неизвестен один.

Таким образом, плоская кинематическая цепь, состоящая из кинематических пар 5 и 4 классов, имеет 2Р₅ + Р₄ неизвестных величин сил реакций.

В то же время для одного звена можно составить 3 уравнения статики, а для n звеньев – 3n уравнений статики.

Кинематическая цепь будет статически определима, если число неизвестных величин сил реакций не превышает числа возможных уравнений статики, то есть

3n = 2P₅ + Р₄

Это есть условие статической определимости кинематической цепи. Полученное равенство можно записать в следующем виде:

3n – 2Р₅ – Р₄ = 0.

Но запись слева от знака равенства является числом степеней свободы кинематической цепи W, то есть

W = 3n – 2Р₅ – P₄ = 0.

Как известно из темы о структуре механизмов (см. раздел 1 «Структура и классификация механизмов»), таким свойством (W=0) обладают структурные группы (или группы Ассура). То есть группы Ассура являются статически определимыми кинематическим цепями.

Поэтому метод силового анализа, приведенный ниже, называется кинетостатическим, так как для определения сил реакций в кинематических парах, возникающих при движении звеньев, используются уравнения статики.

Порядок (последовательность) силового анализа рычажного механизма:

1. Выделяем из механизма последнюю (крайнюю, наиболее удаленную от ведущего звена) структурную группу и проводим её силовой расчёт, используя уравнения статики.

2. Выделяем из механизма следующую структурную группу и проводим её силовой расчёт.

3. Силовой расчёт заканчиваем силовым расчётом ведущего звена.

 

Пример

Задан шестизвенный рычажный механизм (рис. 3.3), состоящий из начального механизма (звенья 0 и 1) и структурных групп, образованных звеньями 2 и 3 (двухповодковая структурная группа 2 класса, 1 вида) и 4, 5 (структурная группа 2 класса, 2 вида).

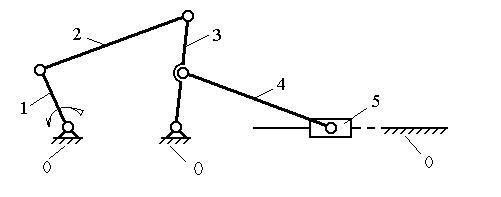
Рис. 3.3. Шестизвенный рычажный механизм

Последовательность силового анализа:

1. Проводим силовой расчёт структурной группы 4-5 (то есть определяем неизвестные реакции, если известны внешние силы, действующие на звенья 4 и 5):

2. Проводим силовой расчёт структурной группы 2-3:

3. Проводим силовой расчёт ведущего звена:

3.3. Силовой анализ характерных структурных групп

3.3.1. Структурная группа 2-го класса 1-го вида

Известны: внешние силы и , а также точки их приложения К₂ и К₃.

Найти: реакции в кинематических парах А, В и С (рис.3.4.).

 

Последовательность решения:

1. Строим структурную группу в масштабе длин m_L (рис.3.4).

2. Наносим на неё все внешние силы и .

3. В кинематических парах А и С действие отброшенных звеньев (например, кривошипа 1 и стойки 0) заменяем силами реакций и , разложив каждую из них на нормальную и тангенциальную составляющие: = + и = + .

4. Составляем уравнение равновесия структурной группы:

; или (3.1)

5. Вычисляем величины тангециальных сил; для этого используем условие, что моменты сил относительно точки В, приложенных к звеньям 2 и 3, равны нулю:

; , откуда ;

; , откуда .

Следует учитывать, что если в процессе решения эти тангенциальные силы получись с отрицательным знаком, то на плане структурной группы их предварительно выбранное направление следует поменять на противоположное.

6. Неизвестные и находим путём графического изображения векторного уравнения (3.1) в масштабе, то есть, строим план сил структурной группы.

Для построения плана сил выбираем масштаб плана сил: , Н/м, где – длина вектора в мм, изображающего силу на плане сил, выбирается произвольно. При выборе учитываются два условия: чтобы план сил разместился на отведённом месте чертежа, а масштаб был удобен для расчётов (был «круглым» числом).

Переводим (пересчитываем) силы уравнения (3.1) в векторные отрезки с длинами: , мм; , мм; , мм.

Тогда уравнение (3.1) запишется в виде

(3.2).

Построение плана сил ведём в последовательности написания уравнения (3.2) (рис. 3.5).

7. Вычисляем реакции:

,

где длины отрезков и берем в мм из плана сил.

8. Определяем реакцию в кинематической паре В. Для этого составляем векторное уравнение равновесия звена 2 или звена 3; например, условие равновесия звена 2 можно записать в виде:

, (3.3).

где R_3-2 – сила реакции в кинематической паре В.

Так как и известны, то, построив план сил звена 2 (рис. 3.6), то есть графически изобразив уравнение (3.3), получим силу :

.

 

Рис. 3.4. План структурной группы 2 класса 1 вида

 

 

Рис. 3.5. План сил структурной группы Рис. 3.6. План сил звена 2

3.3.2. Структурная группа 2-го класса 2-го вида

Рис. 3.7. План структурной группы 2 класса 2 вида

 

 

Условие равновесия структурной группы (рис. 3.7):

. (3.4)

Величина тангенциальной составляющей силы реакции в шарнире вычисляется по формуле, полученной из условия равенства нулю моментов всех сил, приложенных к шатуну 4, относительно точки F:

 

; ,

 

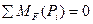откуда находим ,

где h₄ – плечо силы Р₄ относительно точки F, берется из плана структурной группы (рис.3.5.), построенной в масштабе длин m_L.

 

Силы и берут из плана сил, построенного с использованием уравнения (3.4) в выбранном масштабе , а силу находят из уравнения равновесия ползуна , построив план сил ползуна.

3.3.3. Структурная группа 2-го класса 3-го вида

Рассмотрим условие равновесия звена 3 (рис.3.8.):

(3.5.)

Здесь сила задана. Из условия равенства нулю всех моментов сил звена 3 относительно точки В находим силу , предполагая, что без учета трения ее вектор перпендикулярен АВ: ; ; причём h₃ – плечо момента силы P₃, . Отсюда .

Силу реакции между звеньями 1 (кривошипом) и 2 (ползуном) находим из условия . Силу реакции R_0-3 между коромыслом 3 и станиной можно найти, построив план сил, используя уравнение (3.5.) равновесия звена 3.

 

Рис. 3.8. План структурной группы 2 кл. 3 вида

3.3.4. Силовой анализ ведущего звена

Вариант 1. Ведущее звено – зубчатое колесо или кривошип

Рис. 3.9. План кривошипа с приложенными силами

 

На изображенном плане кривошипа (рис. 3.9) сила реакции в кинематической паре А .

Силу берём из силового анализа, проведённого ранее для присоединённой к кривошипу структурной группы. Сила реакции || OA (исходя из теоремы о трёх силах, в соответствии с которой линии сил, действующих на тело, находящееся в равновесии, пересекаются в одной точке. В данном случае это точка А).

Условие равновесия звена 1 (кривошипа):

. (3.6)

Строим план сил звена 1 в масштабе (рис. 3.10), предварительно записав уравнение равновесия (3.6) в виде векторных отрезков:

.

Уравновешивающая сила вычисляется по формуле

,

а реакция в кинематической паре О - по формуле

,

где величины и берутся измерением на плане сил (рис. 3.10.)

Рис. 3.10. План сил кривошипа

Вариант 2. Ведущее звено – муфта скольжения, совмещённая с кривошипом

В этом случае вместо уравновешивающей силы к ведущему звену приложен уравновешивающий момент (рис. 3.11).

R0-1

 

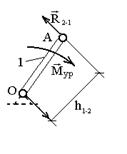
Рис. 3.11. План муфты с кривошипом

Уравнения равновесия ведущего звена 1:

,

,

где h_2-1 – плечо силы R_2-1 относительно оси вращения кривошипа О,

откуда , .

Для нахождения величины плеча h_2-1 можно построить план звена в масштабе, нанести силы и провести необходимые измерения.

 

 

3.4. Теорема о «жёстком» рычаге Жуковского

Теорема используется для определения уравновешивающей силы или уравновешивающего момента без предварительного определения реакций в кинематических парах механизма.

Она является графической интерпретацией принципа возможных перемещений точек приложения сил. Для реального механизма эти возможные перемещения являются реальными.

 

Вывод теоремы

 

Исходя из принципа сохранения энергии сумма работ всех внешних сил, приложенных к звеньям механизма, равна нулю; это условие можно записать в виде

, (3.7)

где P_i – все внешние силы, в том числе силы полезного и вредного сопротивления, силы инерции и веса, действующие на звенья механизма (силы реакции здесь не учитываются);

dS_i – элементарные перемещения точек приложения этих сил;

a_i – угол приложения внешних сил, или угол давления (угол между вектором силы и вектором скорости).

Разделим уравнение (3.7) на бесконечно малый интервал времени dt и получим (при условии, что dS/dt = )

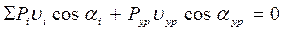, (3.8)

то есть сумма мгновенных мощностей равна нулю.

Для определения величины мгновенных мощностей можно также выполнить решение следующей графической интерпретации. Дано звено ВС с известной скоростью точки D и приложенной к этой точке силой (рис. 3.12). Построим план скоростей, повёрнутый на 90⁰; здесь ; . Вычислим момент силы относительно полюса Р_v плана скоростей:

. (3.9)

С учётом этого уравнение (3.8) можно записать так:

. (3.10)

Так как масштаб , то можно сформулировать теорему Жуковского:

– запись теоремы Жуковского (3.11)

 

или: алгебраическая сумма моментов всех внешних сил, перенесенных с механизма в соответствующие точки повёрнутого на 90⁰ плана скоростей, относительно полюса равна нулю.

Рис. 3.12. План звена с повёрнутым на 90⁰ планом скоростей

Последовательность определения P_ур в механизме по теореме Жуковского:

 

1. Построить повёрнутый на 90⁰ (в любую сторону) план скоростей механизма.

2. В соответствующие точки плана скоростей нанести все ранее определённые внешние силы (включая силы инерции и силы веса), действующие на механизм, в том числе и уравновешивающую силу P_ур.

3. Составить уравнение вида (3.11). Плечи моментов сил брать из повёрнутого плана скоростей.

4. Из составленного уравнения определить P_ур.

Пример

Заданы внешние силы, действующие на звенья механизма Р₂ и Р ₃. Найдём уравновешивающую силу Р_ур. Для этого построим план механизма в масштабе длин (рис. 3.13) и повёрнутый на 90⁰ план скоростей (рис. 3.14).

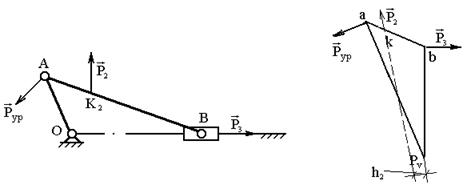
Рис. 3.13. План механизма Рис. 3.14. Повёрнутый на 90⁰

план скоростей

Наносим силы в соответствующие точки k и b₃ повёрнутого плана скоростей, обозначаем плечи сил. Составляем уравнение моментов сил относительно полюса плана скоростей

, отсюда

.

Если силу P_ур получим с отрицательным знаком, то её предварительно выбранное направление следует поменять на противоположное.

 

3.5. Силовой анализ механизма с учетом сил трения

3.5.1. Теоретические основы определения коэффициента трения

Трение в поступательной кинематической паре

 

При перемещении одного тела (звена механизма) относительно находящегося с ним в контакте другого тела (звена) в месте их контакта возникает сила, сопротивляющаяся перемещению. Эту силу назовем силой трения F (рис.3.15.).

Величину коэффициента трения в поступательной кинематической паре можно определить с помощью так называемого закона Кулона, в соответствии с которым величина силы трения F прямо пропорциональна нормальной силе N между соприкасающимися звеньями. Векторная сумма сил и равна полной силе реакций в кинематической паре: (рис.3.15.).

 

 

Рис.3.15. Схема сил в поступательной

кинематической паре

Отношение 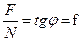называют коэффициентом трения скольжения в поступательной кинематической паре. При этом угол называют углом трения скольжения.

Как видно из рисунка, полная реакция отклоняется на угол трения в сторону, противоположную скорости .

Величину коэффициента трения скольжения f можно определить различными способами:

а) экспериментально;

б) по справочникам (величина f зависит от шероховатости, материалов, трущихся поверхностей, наличия смазки, ее качества, температуры и т.д.).

 

Трение во вращательной кинематической паре

Картину внешних нагрузок, действующих на вал при его вращении, можно условно проиллюстрировать приведенной на рис.3.16 схемой. Здесь:

А – точка приложения нормальной реакции , причем

– равнодействующая всех нормальных сил (эпюра этих сил может иметь различный вид) (рис.3.17.);

–сила трения (равнодействующая всех сил трения, распределенных по поверхности контакта);

– сила давления цапфы вала на опору (корпус подшипника);

 

 

Рис.3.16. Схема сил во вращательной кинематической паре

 

 

– сила реакции во вращательной кинематической паре,

; ;

– угол трения;

r – радиус цапфы (опорной части) вала;

– радиус круга трения;

– приведенный коэффициент трения.

Как видно из схемы (рис.3.14), во вращательной кинематической паре реакция отстоит от оси вращения на величину радиуса круга трения . Причем всегда касательна к кругу трения.

 

Момент трения .

Величину можно определить:

а) экспериментально (например, используя метод выбега, который описан в «Лабораторном практикуме по теории механизмов и машин») [6]:

б) по следующим эмпирическим формулам с учетом износа подшипника и соответствующего изменения эпюр давления (рис.3.17.):

- для нового подшипника: ;

- для уже работавшего подшипника: ,

 

где f – коэффициент трения скольжения в поступательной кинематической паре (берется из справочников).

 

новый подшипник изношенный подшипник

 

Рис.3.17. Примерные схемы эпюр давления в новом и изношенном подшипниках скольжения

 

Трение качения в высшей кинематической паре

Картину внешних сил и эпюр распределения давлений в месте контакта тел качения можно условно отобразить на нижеприведенных схемах. (рис.3.18.). В состоянии покоя эпюра напряжений в зоне контакта симметрична относительно общей нормали, проведенной через условную точку касания, а равнодействующая сила N совпадает с нормалью. При качении симметрия эпюры нарушается, а сила N смещается в направлении качения на расстояние k.

 

а) состояние покоя; б) состояние перекатывания

 

Рис.3.18. Примерные схемы сил и эпюр давления в зоне контакта цилиндра с плоскостью

 

 

Условные обозначения на схемах:

 

– равнодействующая сила давлений в месте смятия соприкасающихся звеньев (тел качения);

– нагружающая сила; ;

– момент трения качения,

– плечо силы трения качения или коэффициент трения качения (имеет размерность длины),

– сила перекатывания.

Условие равновесия перекатывающегося тела в форме моментов можно записать так: , откуда .

Величину можно взять в инженерных справочниках.

3.5.2. Пример учета сил трения при силовом анализе механизма

Пусть задан кривошипно – ползунный механизм с известными внешними силами (рис. 3.19). Необходимо провести силовой анализ механизма, учитывая силы трения в кинематических парах.

А

Ввр., Впост.

Рис.3.19. Кинематическая схема кривошипно – ползунного механизма

 

Последовательность решения следующая. Сначала проводим силовой анализ механизма без учета сил трения (см. примеры, приведенные выше). При этом также определяем силы реакций в кинематических парах. Затем обозначим силы реакций в кинематических парах, радиусы цапф валов и коэффициенты трения и занесем их в таблицу:

 

Кинематические пары Параметры	О	А	Ввр.	Впост.
Силы реакций	R0	RA	RBвp.	RBпост.
Радиусы цапф	r0	rA	rB	-
Коэффициенты трения	f0	fA	fBвр.	fBпост.

Отразим трение в потерях мгновенных мощностей на трение в кинематических парах: вращательной - N = М_тр. × ω; поступательной - , где

М_тр. = R × ρ = R × r × f – момент трения во вращательной кинематической паре,

- сила трения в поступательной кинематической паре.

Применительно к кривошипно – ползунному механизму (рис.3.19) можно выразить потери мощностей на трение следующим уравнением:

N₀ + N_A + N_В^вр. + N_B^пост. = М_тр. × ω₁,

 

где N₀, N_A, N_В^вр., N_B^пост. – соответственно потери мощности на трение в кинематических парах О, А, В^вр., В^пост.,

ω, - угловая скорость кривошипа,

М_тр. – приведенный к кривошипу момент от всех сил трения в кинематических парах.

Тогда уравнение мощностей можно записать в следующем виде:

 

R₀ × r₀ × f₀ × ω₁ + R_A × r_A × f_A × (ω₁ – ω₂) + R_B^вр. × r_B^вр. × f_B^вр. × ω₂ +

+R_B^пост. × f_B^пост. × V_B = M_тр. × ω₁.

Из этого уравнения определяем момент трения М_тр. на ведущем звене, который затем учитывается при расчете уравновешивающего момента М_{ур .} или уравновешивающей силы Р_ур. на ведущем звене механизма.