Способы нахождения ранга.

Обратная матрица.

Опр.: Квадратная матрица, определитель которой det A 0 называется невырожденной.

Опр.: Всякая невырожденная квадратная матрица (det_A 0) имеет обратную. Для обратной матрицы принято обозначение .

Опр.: Матрица называется обратной к матрице A, если произведение равно единичной матрице. Обратная матрица находится по формуле:

Опр.: Матрица называется союзной матрицей. Это транспонированная матрица, состоящая из алгебраических дополнений.

=

Пример:

Найти А^-1 если А=

det A= =10 0, матрица имеет обратную.

А₁₁=(-1)¹⁺¹4=4 А₂₁=(-1)²⁺¹2=(-2)

А₁₂=(-1)¹⁺²1=(-1) А₂₂=(-1)²⁺²3=3

 

Матричный способ решения системы.

Пусть дана система из n –уравнений и n – неизвестных.

(1)

где - числа, - свободные члены, - неизвестные.

Опр.: Решением системы (1) является любой набор чисел x₁, x₂…x_nпри подстановке которого в систему, каждое уравнение системы обращается в тождество.

Опр.: Если система имеет решение, то ее называют совместной. Систему, не имеющую решения, называют несовместной. Совместная система может иметь единственное решение, а может иметь множество решений. Запишем систему в матричном виде.

 

Введем матрицы:

А= Х= В=

(n n) (n 1) (n 1)

 

AX=B (2)

(2) – матричное уравнение системы.

Таким образом, нахождение решения системы уравнений (1) сводится к нахождению матрицы Х из системы(2).

 

Теорема: Если det A 0 тогда система (2), а следовательно, и (1) имеет единственное решение которое находится по формуле

Х=А^-1В

Доказательство:

Умножаем обе части уравнения AX=B на А^-1

Получим А^-1(АХ)=А^-1В тогда (А^-1А)Х=А^-1В ЕХ= А^-1В или

 

Х=А^-1В

 

 

Пример: Решить систему матричным способом.

А= Х= В=

АХ=В – матричная запись системы.

Х=А^-1В – решение системы.

А^-1= ; detA= (1–строку 3 и вычтем из 2–ой)= = = (разложим по элементам 1 – го столбца)= =

система имеет единственное решение.

Найдем А^-1. Для этого надо найти союзную матрицу .

Исходная матрица А= . Найдем алгебраические дополнения к каждому элементу матрицы:

 

Х= = А^-1В= получили

 

Метод Крамера.

Теорема: Если detA 0, тогда система (1) имеет единственное решение, которое находится по формуле:

Δ=detA; – получается при замене в определителе i – го столбца, столбцом свободных членов.

Для системы третьего порядка будем иметь три значения

 

;

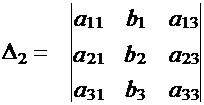
Аналогично получим Δ₃.

Ранг матрицы.

Ранг матрицы отвечает на следующие вопросы:

1. Что можно сказать о существование решения системы, когда detA=0?

2. Как решать систему, состоящую из m – уравнений и n–неизвестных?

Опр.: Пусть A = () – прямоугольная матрица размера m n. Зафиксируем число k, так что k m, и k n. Выделим из данной матрицы любые kстрок и kстолбцов. Определитель составленный из элементов, стоящих на пересечении выделенных kстрок и kстолбцов называется минором k– го порядка.

 

Например пусть дана матрица А размерности 3×4.

А=(3 4); А= ; выберем минор 2 – го порядка

k=2 М= или и т.д.

У матрицы (3 4) можно найти 18-ть миноров второго порядка. Среди этих миноров могут встретиться равные 0, например 0

Опр.: Рангом матрицы называется наибольший порядок отличного от нуля минора.

Из определения следует, что если r(A)=k, то среди всех миноров k – го порядка, хотя бы один отличен от нуля.

Пример:

А= Матрица размерности . Наибольший порядок минора равен трем. Всего таких миноров у данной матрицы 4-е. Следовательно, ранг r(A) 3. Найдем хотя бы один из миноров третьего порядка 0.

Следовательно, r(A)=3

Способы нахождения ранга.

1. Метод окаймляющих миноров.

Сначала находят минор k– го порядка не равный 0, затем вычисляют все окаймляющие миноры (k+1). Если они равны нулю, то все миноры более высоких порядков равны нулю. Тогда r(A)=k. Если среди (k+1) – го порядка найдется минор не равный 0, надо рассматривать все (k+2) – го порядка и т.д.

Пример:

А=

(3 5)

r(A) 3 Выберем минор, т.к. М= тогда М= окаймляющий минор М₃= но другой М₃= следовательно r(A)= 3.

 

2. Метод элементарных преобразований.

Опр. Элементарными преобразованиями называются следующие преобразования:

1.Транспонирование – замена строк столбцами;

2. Перестановка двух строк или двух столбцов;

3. Умножение всех элементов строки или столбца на число не равное 0;

4. Прибавление ко всем элементам строки или столбца соответствующих элементов другой строки или столбца умноженных на одно и тоже число.

Теорема. При элементарных преобразованиях ранг матрицы не меняется.

Если в результате элементарных преобразований получена единичная матрица вида

То ее ранг будет равен числу единиц на главной диагонали

Если в результате элементарных преобразований получена ступенчатая (треугольная) матрица

,то ранг равен числу не нулевых элементов на главной диагонали.

Опр. Минор, с помощью которого устанавливается ранг матрицы, называется базисным минором. Базисных миноров может быть несколько.

Пример: Найти ранг.

 

3 Нахождение ранга матрицы с помощью теоремы о ранге.

Теорема (о ранге матрицы). Если ранг матрицы равен r, то в этой матрице можно найти r линейно независимых строк (столбцов) через которые линейно выражаются остальные ее строки (столбцы).

 

 

Пример: Найти ранг.

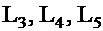строки данной матрицы являются линейно зависимыми так как между ними имеется следующая зависимость или или видим, что строки - линейно выражаются через . Следовательно линейно независимы и по теореме о ранге – ранг равен двум .