Неравенство Коши – Буняковского.

Примеры линейных пространств.

1. Совокупность векторов, лежащих на одной прямой, образует линейное пространство, т.к. сложение векторов и умножение вектора на число приводят снова к векторам, лежащим на одной прямой. Свойства 1-8 легко проверяются. Обозначим L₁, пространство размерности d(L)=1.

2. Совокупность векторов, лежащих на одной плоскости также оказывается замкнутой относительно операций сложения и умножения на число. И образует линейное пространство размерности d(L)=2.

3. Совокупность всех векторов пространства является линейным пространством размерности d(L)=3.

4. Совокупность всех многочленов степени n.

для которых обычным образом введены операции сложения и умножения на число образует линейное пространство.

6 Множество непрерывных функций на [а, в].

7 Множество матриц размера является замкнутым относительно операций сложения и умножения на число, т.е. образует линейное пространство (для доказательства матричные единицы нумеруются в каком – либо порядке).

Опр.: Непустое пространство векторов L^¢из L, которые сами образуют линейное пространство, называется подпространством линейного пространства.

Размерность подпространства не превосходит размерности пространства.

Для того чтобы убедится в том, что L^¢ является подпространством пространства L достаточно проверить операцию сложения и умножения на число. Все пространство L одновременно можно считать подпространством.

Задача 1: Образуют ли подпространство линейного пространства векторы лежащие в плоскости XOY, начало которых совпадают с началом координат, а концы лежат в первом квадрате.

		Решение: проводим операцию сложения: сумма первому квадрату: произведение первому квадрату, если <0. Ответ: не образует.

Задача 2: Образует ли подпространство линейного пространства совокупность векторов, для которых .

Решение: Проверим: 1) операцию сложения: , .

2) операцию умножения на число: ;

Можно показать, что все восемь аксиом выполняются.

Ответ: образует.

Задача 3: Образует ли линейное пространство совокупность векторов, для которых .

Решение: Не образует, т.к. нарушается аксиома 3. В таком пространстве не существует нулевой элемент О=(0,…,0), поскольку: S0¹1.

Евклидово пространство.

Определим операцию скалярного умножения векторов, а длину и угол введем с помощью этого определения.

Опр.: Линейное пространство называется Евклидовым, если в нем определена операция скалярного умножения: любым двум векторам , 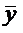из Lсопоставляется число (, 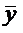) и выполняются следующие условия. Для " и числа aвыполняются аксиомы:

1.

2.

3.

4. 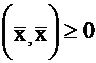, из условия , вытекает, что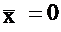

Опр.: Длиной, модулем или нормой вектора в Евклидовом пространстве.

Опр.: Угол между векторами определим как

Надо показать, что

Для этого докажем неравенство Коши – Буняковского .

Неравенство Коши – Буняковского.

Неравенство Коши – Буняковского .

Доказательство: рассмотрим вектор ;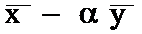

из аксиомы 4 (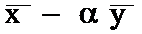, 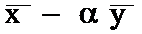) , применяя аксиомы 1-3, получим:

- это квадратное

неравенство, относительно . Неравенство выполняется, когда D 0

- это неравенство типа:

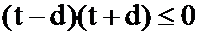, или , или

, что и требовалось доказать.

В Евклидовом пространстве справедливо неравенство треугольника