ЛЕКЦИИ ПО ДИСЦИПЛИНЕ
«Математический анализ»
для направления 080100 «Экономика»
Рязань 2012
Тема 9. Числовые и степенные ряды
Числовой ряд, его сходимость.
Простейшие свойства сходящихся числовых рядов
Пусть  – бесконечная числовая последовательность. Построим из этой последовательности новую последовательность по правилу
– бесконечная числовая последовательность. Построим из этой последовательности новую последовательность по правилу
 ,
,  ,
,  , …,
, …,  , …
, …
Определение 1. Числовым рядом называют упорядоченную пару числовых последовательностей  . Числа
. Числа 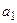 ,
,  , …
, … 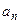 , … называют членами ряда. Правило построения числа
, … называют членами ряда. Правило построения числа 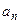 называют общим членом ряда. Число
называют общим членом ряда. Число  называют
называют  -ой частичной суммой ряда.
-ой частичной суммой ряда.
Замечание. Числовой ряд обозначают символом  .
.
Определение 2. Числовой ряд называют сходящимся, если существует конечный предел последовательности его частичных сумм.
Определение 3. Числовой ряд называют расходящимся, если предел последовательности его частичных сумм или не существует или равен  .
.
Определение 4. Если числовой ряд сходится, то предел последовательности его частичных сумм называют суммой ряда 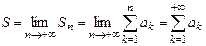 .
.
Замечание. Если числовой ряд расходится, а предел его частичных сумм равен  (
( ), то говорят, что сумма ряда равна
), то говорят, что сумма ряда равна  (
( )
)
Свойства сходящихся числовых рядов
1. Отбрасывание конечного числа первых членов числового ряда не влияет на сходимость (расходимость) ряда.
2. Если числовой ряд  сходится и имеет сумму
сходится и имеет сумму  , то сходится также и ряд
, то сходится также и ряд  , где
, где 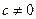 – постоянное число, причем сумма ряда
– постоянное число, причем сумма ряда  равна
равна 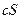 .
.
3. Если числовые ряды  и
и  сходятся, и суммы их соответственно равны
сходятся, и суммы их соответственно равны  и
и  , то ряд
, то ряд  тоже сходится и имеет сумму
тоже сходится и имеет сумму 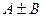 .
.
Замечание. Теория числовых рядов решает две задачи: 1) выяснить, сходится ряд или нет; 2) если ряд сходится, вычислить его сумму.
Признаки сходимости числовых рядов
Теорема 1 (необходимое условие сходимости). Если числовой ряд  сходится, то
сходится, то  .
.
Замечание. На практике теорему используют следующим образом: вычисляют 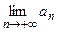 . Если
. Если  , то ряд
, то ряд  расходится. Если
расходится. Если  , то вопрос о сходимости ряда остается открытым.
, то вопрос о сходимости ряда остается открытым.
Определение 5. Числовой ряд, все члены которого положительны (неотрицательны) называют положительным (неотрицательным) числовым рядом.
Теорема 2 (Первый признак сравнения). Пусть даны два неотрицательных числовых ряда  и
и  , причем для любого номера
, причем для любого номера 
 . Тогда, если ряд
. Тогда, если ряд  сходится, то сходится ряд
сходится, то сходится ряд  . Если ряд
. Если ряд  расходится, то ряд
расходится, то ряд  также расходится.
также расходится.
Теорема 3 (Второй признак сравнения). Пусть даны два неотрицательных числовых ряда  и
и  , и пусть
, и пусть  . Тогда оба ряда сходятся или расходятся одновременно.
. Тогда оба ряда сходятся или расходятся одновременно.
Замечание 1. Если в условиях теоремы 3  , то если ряд
, то если ряд 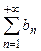 сходится, то сходится ряд
сходится, то сходится ряд  ; если ряд
; если ряд  расходится, то ряд
расходится, то ряд 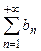 также расходится.
также расходится.
Замечание 2. Если в условиях теоремы 3 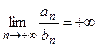 , то если ряд
, то если ряд  сходится, то сходится ряд
сходится, то сходится ряд 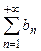 ; если ряд
; если ряд 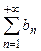 расходится, то ряд
расходится, то ряд  также расходится.
также расходится.
Замечание 3. Исследуемый числовой ряд обычно сравнивают с неотрицательным числовым рядом, сходимость (расходимость) которого установлена отдельно. Такие ряды будем называть базовыми.
Базовые ряды
1. Ряд  называют гармоническим. Он является расходящимся.
называют гармоническим. Он является расходящимся.
2. Ряд 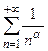 называют обобщенным гармоническим. Он является расходящимся при
называют обобщенным гармоническим. Он является расходящимся при 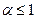 и сходится при
и сходится при 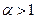 .
.
3. Ряд  называют геометрической прогрессией. Он является расходящимся при
называют геометрической прогрессией. Он является расходящимся при  и сходится при
и сходится при  (его сумма
(его сумма  ).
).
Пример 1. Найти сумму ряда  , пользуясь определением.
, пользуясь определением.
Решение. Рассмотрим общий член ряда:  . Разложим его на сумму простых дробей:
. Разложим его на сумму простых дробей:  . Найдем коэффициенты
. Найдем коэффициенты  и
и  методом неопределенных коэффициентов. Имеем
методом неопределенных коэффициентов. Имеем  . Приравнивая коэффициенты при одинаковых степенях
. Приравнивая коэффициенты при одинаковых степенях  , получаем
, получаем  ,
,  . Отсюда
. Отсюда  ,
,  и
и  .
.
Выпишем  -ю частичную сумму ряда:
-ю частичную сумму ряда:
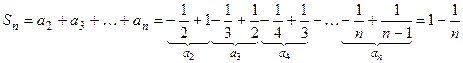 .
.
Найдем сумму ряда:  .
.
Пример 2. Найти сумму ряда  , пользуясь определением.
, пользуясь определением.
Решение. Рассмотрим общий член ряда:  . Выпишем
. Выпишем  -ю частичную сумму ряда: при
-ю частичную сумму ряда: при  четном (
четном ( ,
,  )
) 
 ; при
; при  нечетном (
нечетном (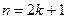 ,
,  )
) 
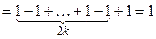 . Тогда
. Тогда 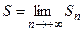 не существует. Следовательно, исследуемый ряд расходится.
не существует. Следовательно, исследуемый ряд расходится.
Пример 3. Исследовать ряд  на сходимость.
на сходимость.
Решение. Проверим необходимое условие сходимости. Так как  , следовательно, необходимое условие сходимости не выполняется, ряд расходится.
, следовательно, необходимое условие сходимости не выполняется, ряд расходится.
Пример 4. Исследовать ряд  на сходимость.
на сходимость.
Решение. Проверим необходимое условие сходимости. Так как 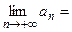
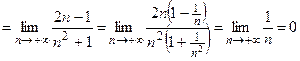 , необходимое условие сходимости выполняется.
, необходимое условие сходимости выполняется.
Сравним исходный ряд с гармоническим рядом  . По второй теореме сравнения получаем
. По второй теореме сравнения получаем  . Так как гармонический ряд расходится, то и исследуемый ряд расходится.
. Так как гармонический ряд расходится, то и исследуемый ряд расходится.
Пример 5. Исследовать ряд  на сходимость.
на сходимость.
Решение. Проверим необходимое условие сходимости. Так как 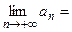
 , необходимое условие сходимости выполняется.
, необходимое условие сходимости выполняется.
Сравним исходный ряд с обобщенным гармоническим рядом  (
(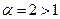 ). По второй теореме сравнения получаем
). По второй теореме сравнения получаем 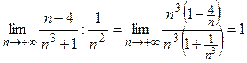 . Так как обобщенный гармонический ряд при
. Так как обобщенный гармонический ряд при  сходится, то и исследуемый ряд сходится.
сходится, то и исследуемый ряд сходится.
Теорема 4 (признак Коши). Пусть для положительного числового ряда  существует
существует 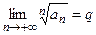 . Если
. Если  , то ряд сходится. Если
, то ряд сходится. Если  , то ряд расходится. Если
, то ряд расходится. Если  , то вопрос о сходимости ряда остается открытым.
, то вопрос о сходимости ряда остается открытым.
Теорема 5 (признак Даламбера). Пусть для положительного числового ряда  существует
существует  . Если
. Если  , то ряд сходится. Если
, то ряд сходится. Если  , то ряд расходится. Если
, то ряд расходится. Если  , то вопрос о сходимости ряда остается открытым.
, то вопрос о сходимости ряда остается открытым.
Пример 6. Исследовать ряд  на сходимость.
на сходимость.
Решение. Проверим необходимое условие сходимости. Так как  (см. тему 8, значения базовых пределов), необходимое условие сходимости выполняется. Воспользуемся признаком Даламбера:
(см. тему 8, значения базовых пределов), необходимое условие сходимости выполняется. Воспользуемся признаком Даламбера:
 ,
,
следовательно, ряд сходится.
Теорема 6 (интегральный признак Коши). Если для неотрицательного числового ряда  существует неотрицательная, нестрого убывающая функция
существует неотрицательная, нестрого убывающая функция  , определенная на промежутке
, определенная на промежутке 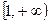 , такая, что для каждого номера
, такая, что для каждого номера 
 , то несобственный интеграл
, то несобственный интеграл  и ряд
и ряд  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример 7. Исследовать ряд  на сходимость.
на сходимость.
Решение. Проверим необходимое условие сходимости. Так как  , то необходимое условие сходимости выполняется. Воспользуемся интегральным признаком Коши. Тогда функция
, то необходимое условие сходимости выполняется. Воспользуемся интегральным признаком Коши. Тогда функция  определена на промежутке
определена на промежутке 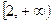 и удовлетворяет всем условиям теоремы 6. Вычислим несобственный интеграл:
и удовлетворяет всем условиям теоремы 6. Вычислим несобственный интеграл:
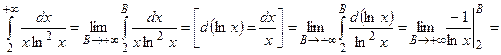
 .
.
Несобственный интеграл сходится, следовательно, ряд  тоже сходится.
тоже сходится.
Знакочередующиеся ряды
Определение 6. Числовой ряд, имеющий бесконечное число как положительных, так и отрицательных членов, называют знакопеременным.
Определение 7. Числовые ряды вида  и
и  (
( ) называют знакочередующимися.
) называют знакочередующимися.
Определение 8. Знакочередующийся ряд называют рядом типа Лейбница, если 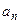 является монотонно убывающей функцией номера и
является монотонно убывающей функцией номера и  (
( ).
).
Теорема 7. Любой ряд типа Лейбница сходится.
Определение 9. Знакопеременный ряд  называют абсолютно сходящимся, если ряд, составленный из абсолютных величин его членов
называют абсолютно сходящимся, если ряд, составленный из абсолютных величин его членов  , сходится.
, сходится.
Определение 10. Знакопеременный ряд  называют условно сходящимся, если он сходится, а ряд
называют условно сходящимся, если он сходится, а ряд  , составленный из абсолютных величин его членов, расходится.
, составленный из абсолютных величин его членов, расходится.
Теорема 8. Если знакопеременный ряд сходится абсолютно, то он сходится.
Пример 7. Исследовать ряд 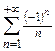 на абсолютную и условную сходимость.
на абсолютную и условную сходимость.
Решение. Исследуем ряд на абсолютную сходимость. Соответствующий ряд  является гармоническим, следовательно, расходится. Значит, ряд
является гармоническим, следовательно, расходится. Значит, ряд 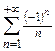 абсолютно расходится.
абсолютно расходится.
Исследуемый ряд является знакочередующимся,  ,
,  , с увеличением номера значения
, с увеличением номера значения  монотонно убывают (
монотонно убывают ( ). Следовательно, ряд
). Следовательно, ряд 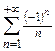 является рядом типа Лейбница, по теореме 7 он сходится. Таким образом, ряд
является рядом типа Лейбница, по теореме 7 он сходится. Таким образом, ряд 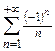 условно сходится.
условно сходится.
Сходимость степенных рядов
Пусть  – бесконечная последовательность функций, определенных на некотором числовом множестве
– бесконечная последовательность функций, определенных на некотором числовом множестве  . Построим из этой последовательности новую последовательность по правилу:
. Построим из этой последовательности новую последовательность по правилу:
 ,
,  , …,
, …,  , …
, …
Определение 1. Функциональным рядом называют упорядоченную пару последовательностей  . Обозначение:
. Обозначение:  .
.
Определение 2. Степенным рядом называют функциональный ряд вида 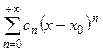 . Вещественные числа
. Вещественные числа  (
( ) называют коэффициентами степенного ряда. Вещественное число
) называют коэффициентами степенного ряда. Вещественное число  называют центром степенного ряда.
называют центром степенного ряда.
Определение 3. Степенной ряд вида 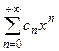 называют рядом Маклорена.
называют рядом Маклорена.
Замечание 1. Если сделать замену переменной 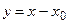 , то от степенного ряда
, то от степенного ряда 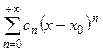 всегда можно перейти к ряду Маклорена вида
всегда можно перейти к ряду Маклорена вида  . Поэтому далее рассматриваем степенные ряды вида
. Поэтому далее рассматриваем степенные ряды вида 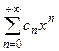 .
.
Замечание 2. Область определения любого степенного ряда – множество всех действительных чисел 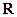 .
.
Замечание 3. Любой степенной ряд вида 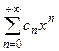 сходится при
сходится при 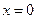 . Одна из задач теории степенных рядов: выяснить, при каких еще значениях
. Одна из задач теории степенных рядов: выяснить, при каких еще значениях  степенной ряд сходится, а также при каких значениях
степенной ряд сходится, а также при каких значениях  степенной ряд сходится абсолютно.
степенной ряд сходится абсолютно.
Теорема 1. Если степенной ряд 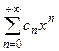 сходится при некотором
сходится при некотором  (
(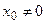 ), то он сходится при любом значении
), то он сходится при любом значении  , удовлетворяющем условию
, удовлетворяющем условию  . Если степенной ряд
. Если степенной ряд 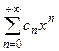 расходится при некотором
расходится при некотором  (
(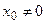 ), то он расходится при любом значении
), то он расходится при любом значении  , удовлетворяющем условию
, удовлетворяющем условию  .
.
Теорема 2. Для всякого степенного ряда 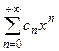 существует число (возможно и бесконечное)
существует число (возможно и бесконечное)  такое, что
такое, что
1) если 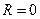 , то ряд сходится только при
, то ряд сходится только при 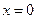 ;
;
2) если 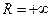 , то ряд сходится при любом
, то ряд сходится при любом  ;
;
3) если 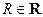 , то при всех
, то при всех  , удовлетворяющих условию
, удовлетворяющих условию  , ряд сходится, а при всех
, ряд сходится, а при всех  ,
,  , удовлетворяющих условию
, удовлетворяющих условию  , ряд расходится.
, ряд расходится.
Определение 4. Число  такое, что при
такое, что при  ряд сходится, а при
ряд сходится, а при 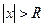 – расходится, называют радиусом сходимости степенного ряда.
– расходится, называют радиусом сходимости степенного ряда.
Определение 5. Интервал  называют интервалом сходимости степенного ряда.
называют интервалом сходимости степенного ряда.
Замечание. Из теоремы 2 следует, что при всех  степенной ряд
степенной ряд  сходится абсолютно, при всех
сходится абсолютно, при всех 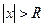 – расходится. При
– расходится. При  вопрос о сходимости должен рассматриваться конкретно для каждого ряда.
вопрос о сходимости должен рассматриваться конкретно для каждого ряда.
Определение 6. Множество точек числовой прямой, получающееся добавлением интервалу сходимости точек  и
и  , называют промежутком сходимости или областью сходимости степенного ряда.
, называют промежутком сходимости или областью сходимости степенного ряда.
Теорема 3. Пусть для степенного ряда 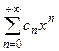 существует предел
существует предел  . Тогда: 1) если
. Тогда: 1) если  , то
, то 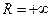 ; 2) если
; 2) если 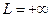 , то
, то 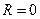 ; 3) если
; 3) если  , то
, то  .
.
Теорема 4. Пусть для степенного ряда 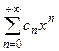 существует предел
существует предел 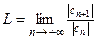 . Тогда: 1) если
. Тогда: 1) если  , то
, то 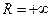 ; 2) если
; 2) если 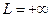 , то
, то 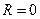 ; 3) если
; 3) если  , то
, то  .
.
Пример 1. Найти промежуток сходимости степенного ряда  .
.
Решение. Найдем радиус сходимости. Так как  , то по теореме 4 имеем
, то по теореме 4 имеем
 .
.
Отсюда 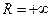 , то есть ряд
, то есть ряд  абсолютно сходится на всей числовой прямой.
абсолютно сходится на всей числовой прямой.
Пример 2. Найти промежуток сходимости степенного ряда  .
.
Решение. 1) Найдем радиус сходимости. Так как  , то по теореме 3 имеем
, то по теореме 3 имеем  . Отсюда
. Отсюда  .
.
2) Интервал сходимости: ряд  абсолютно сходится в интервале
абсолютно сходится в интервале  .
.
3) Исследуем ряд на сходимость в точках  и
и  .
.
При  ряд принимает вид
ряд принимает вид  . Это числовой знакочередующийся ряд, он расходится (см. тему 15, пример 2).
. Это числовой знакочередующийся ряд, он расходится (см. тему 15, пример 2).
При  ряд принимает вид
ряд принимает вид  . Это числовой положительный ряд. Проверим необходимое условие сходимости:
. Это числовой положительный ряд. Проверим необходимое условие сходимости:  , следовательно, ряд расходится.
, следовательно, ряд расходится.
Таким образом, промежутком сходимости является интервал  .
.
Пример 3. Найти промежуток сходимости степенного ряда 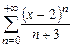 .
.
Решение. 1) Найдем радиус сходимости. Обозначим  и рассмотрим вспомогательный ряд
и рассмотрим вспомогательный ряд  . Так как у вспомогательного ряда
. Так как у вспомогательного ряда  , то по теореме 3 имеем:
, то по теореме 3 имеем:  . Отсюда
. Отсюда  .
.
2) Найдем интервал сходимости ряда 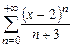 . Так как
. Так как  , то по теореме 2 имеем
, то по теореме 2 имеем 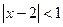 , или
, или  , или
, или  . Ряд
. Ряд 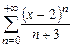 абсолютно сходится в интервале
абсолютно сходится в интервале  .
.
3) Исследуем ряд на сходимость в точках  и
и  .
.
При  ряд принимает вид
ряд принимает вид  . Ряд
. Ряд  является числовым знакочередующимся. Исследуем его на абсолютную сходимость. Соответствующий ряд из абсолютных членов:
является числовым знакочередующимся. Исследуем его на абсолютную сходимость. Соответствующий ряд из абсолютных членов:  . Проверим необходимое условие сходимости:
. Проверим необходимое условие сходимости:  , следовательно, необходимое условие сходимости выполняется. Сравним ряд
, следовательно, необходимое условие сходимости выполняется. Сравним ряд  с гармоническим рядом
с гармоническим рядом  . В силу второй теоремы сравнения получаем
. В силу второй теоремы сравнения получаем  , следовательно, ряд
, следовательно, ряд  расходится, а ряд
расходится, а ряд  расходится абсолютно. Но так как
расходится абсолютно. Но так как  , и с увеличением номера
, и с увеличением номера 
 убывает, то ряд
убывает, то ряд  является рядом типа Лейбница. Следовательно, он сходится. Точку
является рядом типа Лейбница. Следовательно, он сходится. Точку  можно включить в промежуток сходимости.
можно включить в промежуток сходимости.
При  ряд принимает вид
ряд принимает вид  . Это числовой положительный ряд. Необходимое условие сходимости для этого ряда выполняется (
. Это числовой положительный ряд. Необходимое условие сходимости для этого ряда выполняется ( ). Но, сравнивая этот ряд с гармоническим рядом
). Но, сравнивая этот ряд с гармоническим рядом  , в силу второй теоремы сравнения получаем
, в силу второй теоремы сравнения получаем  , следовательно, ряд
, следовательно, ряд  расходится. Точка
расходится. Точка  не входит в промежуток сходимости.
не входит в промежуток сходимости.
Таким образом, промежутком сходимости является полуинтервал  .
.
Теорема 5. Если радиус сходимости степенного ряда не равен нулю, то сумма этого степенного ряда является непрерывной функцией на любом отрезке  .
.