Этот метод используется при расчете многодисковых систем.
Например, для расчета трехдисковой рамы (рис. 3.3 а) проводятся три совместных сечения I, II, III. В результате выявляются девять неизвестных реакций (рис. 3.3 б): опорные реакции R1, R2, H и междисковые реакции X1, X2, X3, Y1, Y2, Y3. Составив для каждого диска по три уравнения равновесия, т.е. 3´3=9 уравнений, из их решения определяются все 9 реакций.
Рис. 3.3
Алгоритм метода совместных сечений:
1) совместными сечениями разделить систему на части (диски);
2) обозначить опорные и междисковые реакции;
3) для каждого диска записать уравнения равновесия;
4) решить систему полученных уравнений;
5) каждый диск рассчитать отдельно и построить эпюры;
6) объединить все эпюры в общие эпюры M, Q, N.
Метод вырезания узла
Используется для определения усилий простых систем.
Сущность метода: вырезается узел с не более чем двумя неизвестными усилиями; силы, действующие в узле, проецируются на две оси; из этих уравнений определяются искомые усилия.
Например, при расчете балочно-ферменной системы (рис. 3.4 а), после того как определены опорные реакции (рис. 3.4 б), вырезается узел А (рис. 3.4 в) и составляются уравнения равновесия:
SX = N2 cos45– N1 cos45= 0,
SY = N1 sin45+ N2 sin45+ P/2 = 0.
Из них определяются искомые продольные силы: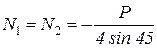 
.
Рис. 3.4
Метод замены связей
Используется при расчете сложных статически определимых систем, которые трудно рассчитать другими способами.
Сущность метода: сложная система превращается в более простую путем перестановки связи (или нескольких связей) в другое место; из условия эквивалентности заданной и заменяющей систем определяется усилие в переставленной связи; затем система рассчитывается известными способами.
Например, для расчета рамы (рис. 3.5 а) удалим правый вертикальный стержень заданной системы (ЗС) и введем одну связь в левый шарнир. Тогда шарнир станет припайкой С, а примыкающие к нему стержни будут жестко связаны. Обозначив усилие в удаленной связи через X, получим так называемую основную систему (ОС) для расчета рамы (рис. 3.5 б).
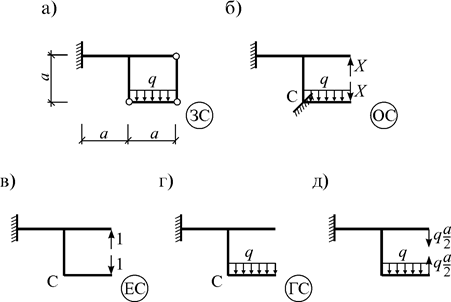
Рис. 3.5
Условием эквивалентности ОС по отношению к ЗС будет условие равенства нулю момента в точке С: MC=0. По принципу суперпозиции этот момент равняется сумме моментов от силы X и внешней нагрузки:
MC=MC,X + MC,P =0.
Теперь рассмотрим два состояния ОС: 
1) единичное состояние (ЕС), где прикладываются силы X=1 (рис. 3.5 в);
2) грузовое состояние (ГС), где прикладывается нагрузка (рис. 3.5 г).
Тогда предыдущее уравнение примет вид
X + MC,P =0,
где 
=1×a=a – момент в точке С в единичном состоянии;
MC,P=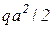 
– момент в точке С в грузовом состоянии.
Теперь неизвестное усилие легко вычисляется:
.
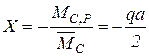После этого можно перейти к расчету более простой системы (рис. 3.5 д).
В более сложных случаях переставляются несколько связей и записываются столько же условий эквивалентности:
s11X1+s12X2+¼+ s1nXn+S1P=0,
s21X1+s22X2+¼+ s2nXn+S2P=0,.................
sn1X1+sn2X2+¼+ snnXn+SnP=0.
Здесь 1, 2, ¼, n – заменяемые связи; X1, X2, ¼, Xn – неизвестные внутренние усилия в этих связях; sij – усилие в связи i в j- ом единичном состоянии; SiP – усилие в i- ой связи в грузовом состоянии.
Из этой системы уравнений определяются неизвестные X1, X2, ¼, Xn.
Общий вывод. Расчет любой статически определимой системы приводит к решению системы n линейных уравнений с n неизвестными. Если определитель полученной системы уравнений отличен от нуля (det¹0), внутренние усилия будут конечными величинами. Если же определитель равняется нулю (det=0), то внутренние усилия определить нельзя. В этом случае система является мгновенно изменяемой.
В о п р о с ы
1. Какая система называется статически определимой?
2. Какие особенности имеет статически определимая система?
3. Какие формы уравнений равновесия можно записать для плоской системы?
4. Что такое изгибающий момент, поперечная сила и продольная сила, как определяются их знаки?
5. Какие методы используются при расчете статически определимых систем?
6. В чем сущность метода замены связей?
7. Какой общий вывод можно сделать после анализа методов расчета статически определимых систем?
Л е к ц и я 4