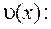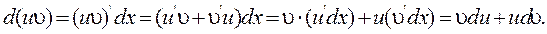В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать, а затем продифференцировать результат. Такую операцию называют логарифмическим дифференцированием.
Пусть функция 
положительна и дифференцируема в данной точке 
. Тогда в этой точке существует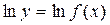 
. Рассматривая 
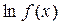как сложную функцию аргумента , мы можем вычислить производную этой функции в данной точке , принимая за промежуточный аргумент. Получаем:
.
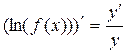Эта величина называется логарифмической производной функции в данной точке .
Вычислим логарифмическую производную степенно-показательной функции 
. Допустим, что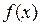 
, 
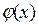- непрерывные и дифференцируемые функции; 
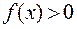. Тогда 
, 
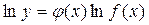. Учитывая, что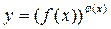 
, получаем: 
.
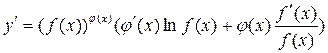Примеры
1) Пусть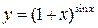 
. Найти 
.
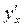Решение. Прологарифмируем данное выражение
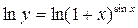
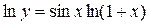
Найдем производную от левой и правой части, считая y зависящей от x.
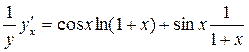
Выразим 
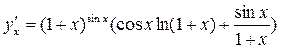
2) Пусть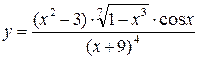 
. Найти .
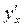При нахождении производной от дроби получим громоздкое выражение, поэтому сначала прологарифмируем функцию.
;
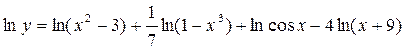Найдем производную от левой и правой части этого уравнения, считая y зависящей от x.
Выразим 
;
.
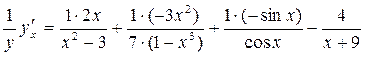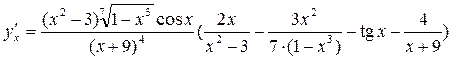3.12. Производная неявной функции
Рассмотрим дифференцирование неявной функции, заданной уравнением 
Для нахождения производной функции y, заданной неявно, нужно продифференцировать обе части уравнения, рассматривая y как функцию от x, а затем из полученного соотношения найти производную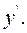 
Пример. Найти производную функции y, заданную уравнением
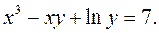
Решение. Дифференцируя обе части равенства и учитывая, что y есть функция от x, получим
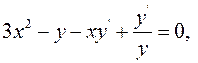откуда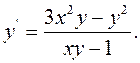 
Замечание. В дальнейших разделах данного пособия нам потребуется понятие производной функции многих переменных. Частная производная функции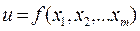 
по аргументу 
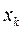является обыкновенной производной функции одной переменной 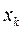при фиксированных значениях других переменных (то есть 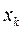считаем аргументом, все остальные 
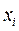- константами). Обозначается такая производная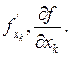 
Теория функции нескольких переменных выходит за рамки данного пособия (см. часть 3).
Дифференциал функции
Пусть функция дифференцируема в точке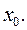 
Тогда по определению (3.2) дифференцируемости функции ее приращение 
в этой точке может быть представлено в виде
(3.4)
где A – некоторое число, не зависящее от приращения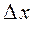 
, а 
бесконечно малая функция пр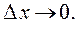и 
Если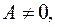 
то при 
величина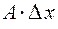 
является бесконечно малой одного порядка с 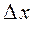, а 
бесконечно малая более высокого порядка малости по сравнению с .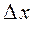
Тогда 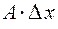будет главной частью приращения , обусловленного приращением аргумента .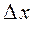
Определение 3.4. Дифференциалом функции в точке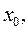 
соответствующим приращению 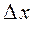аргумента x, называют главную линейную относительность 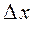часть приращения функции в этой точке
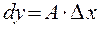
Но по теореме 3.1 имеем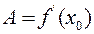 
и можно записать: 
Найдем дифференциал независимой переменной. Пусть 
Тогда:
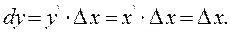
Учитывая, что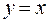 
, получаем:
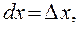
т.е. дифференциал независимой переменной равен её приращению и справедлива запись:
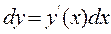(3.8)
Из равенства (3.8) производную 
в любой точке x можно вычислить как отношение дифференциала функции dy к дифференциалу независимой переменной dx:
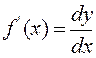, тогда имеем: 
(3.9).
Поскольку дифференциал dy функции отличается от производной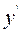 
лишь независящим от x сомножителем dx, то для вычисления дифференциалов можно использовать правила дифференцирования и формулы производных элементарных функций. Например:
1) 
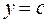
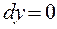
2) 
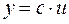
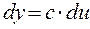
3) 
4) 
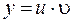
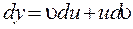
5) 
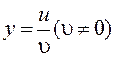
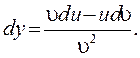
Так, для дифференциала произведения дифференцируемых функци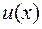й 
и 
