Пусть функция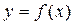 
дифференцируема на интервале (a, b). Тогда существует касательная к графику функции 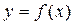в любой точке 
этого графика 
причем, касательная не параллельна оси Oy, поскольку ее угловой коэффициент, равный 
, конечен.
Определение 3.9. Будем говорить, что график функции 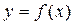имеет на (a, b) выпуклость, направленную вниз (вверх), если он расположен не ниже (не выше) любой касательной к графику функций на (a, b) (рис. 3.23)
 |
Рис. 3.23
Теорема 3.12 Если функция 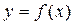имеет на интервале (a, b) вторую производную и 
(
) во всех точках (a, b), то график функции 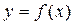имеет на (a, b) выпуклость, направленную вниз (вверх).
Геометрический смысл признака:
, т.е. 
возрастает, график вогнут;
, т.е. убывает, график выпуклый.
Пример
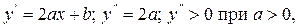график функции вогнут для всех x; 
график выпуклый для всех x.
Замечание. Признак не является необходимым, т.е. в точке выпуклости или вогнутости может быть 
.
Пример. 
(рис. 3.24)
Рис. 3.24
Определение 3.10. Точка 
называется точкой перегиба графика функции 
, если в точке M график имеет касательную, и существует такая окрестность точки 
, в пределах которой график функции слева и справа от точки имеет разные направления выпуклости.
Теорема 3.13. (необходимое условие точки перегиба). Пусть график функции имеет перегиб в точке и пусть функция имеет в точке непрерывную вторую производную. Тогда 
в точке обращается в нуль, т.е. 
Теорема 3.14. (достаточное условие точки перегиба). Пусть функция имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах указанной окрестности имеет разные знаки слева и справа от точки , то график имеет перегиб в точке .
Замечание. Теорема остается верной, если 
имеет вторую производную в некоторой окрестности точки , за исключением самой точки , и существует касательная к графику функции в точке M. Тогда, если в пределах указанной окрестности имеет разные знаки слева и справа от точки , то график функции имеет перегиб имеет перегиб в точке .
Пример. 
; 
В точке 
вторая производная не существует, но слева и справа от нее имеет разные знаки и график функции имеет перегиб в точке (рис. 3.25)
 |
Рис. 3.25
Асимптоты графика функции
При исследовании поведения функции на бесконечности, т.е. при 
или при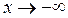 
или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называются асимптотами.
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 3.10. Прямая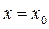 
называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений 
или 
равно 
или 
.
Определение 3.11. Прямая 
называется горизонтальной асимптотой, графика функции при (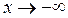), если 
Определение 3.12. Прямая 
называется наклонной асимптотой графика функции при (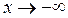), если функцию можно представить в виде
где 
при ().
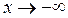Пример
Найти асимптоты графика функции 
Решение
1) - вертикальная асимптота, т.к. 
2) Горизонтальных асимптот нет
3) 
Итак, наклонная асимптота 
Пример
Найти асимптоты графика функции 
Решение. Функция определена на всей числовой оси. Нет вертикальных асимптот.
Найдем наклонные асимптоты 
где 
(т.к. 
)
(т.к. 
)
Замечание: при вычислении пределов использовалось правило Лопиталя. Итак, получены две наклонных асимптоты
