Примеры:
Определение предела функции
При рассмотрении этого учебника, также начну с определения предела функции. Определение предела функции по Коши формулируется следующим образом:«Число A называется пределом функции f(x) при x, стремящемся к  (т.е.
(т.е.  ), если для любого числа
), если для любого числа 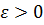 можно подобрать такое число
можно подобрать такое число  , что |f(x)-A|<
, что |f(x)-A|< 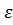 для всех x, удовлетворяющих неравенству
для всех x, удовлетворяющих неравенству  ».
».
Теорема Лагранжа
Формула Лагранжа. Воспользуемся геометрическим смыслом производной, чтобы дать наглядные пояснения справедливости того, что существует касательная к графику f в точке с абсциссой c из интервала (a;b), параллельная секущей, проходящей через точки A(a; f(a)), B(b; f(b)).
Рассмотрим прямуюl, параллельную AB и не имеющую общих точек с частью графика, соответствующей промежутку [a;b]. Будем перемещать эту прямую l по направлению к графику f так, чтобы она оставалась параллельной AB. Зафиксируем положение  этой прямой в момент,
этой прямой в момент,  когда у нее появятся общие точки с этой частью графика. Из рисунка 96(а) видно, что любая из таких «первых» общих точек - точка касания прямой
когда у нее появятся общие точки с этой частью графика. Из рисунка 96(а) видно, что любая из таких «первых» общих точек - точка касания прямой  с графиком f. обозначим абсциссу этой точки через c. Тогда
с графиком f. обозначим абсциссу этой точки через c. Тогда  (c)=tg
(c)=tg  , где
, где  – угол между прямой
– угол между прямой  и осью абсцисс. Но
и осью абсцисс. Но  AB, поэтому угол
AB, поэтому угол  равен углу наклона секущей AB, т.е.
равен углу наклона секущей AB, т.е.


Итак, если функция дифференцируема, то на интервале (a;b) найдется такая точка 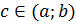 (рис.96 (б)), что
(рис.96 (б)), что

Эта формула называется формулой Лагранжа.

Перед рассмотрением теоремы Ферма стоит дать определение точек максимума и минимума.
Точка 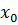 называется точкой минимума функции f, если для всех x из некоторой окрестности
называется точкой минимума функции f, если для всех x из некоторой окрестности 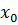 выполнено неравенство
выполнено неравенство  (рис. 42).
(рис. 42).

Точки минимума и максимума функции
Точка 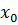 называется точкой максимума функции f, если для всех x из некоторой окрестности
называется точкой максимума функции f, если для всех x из некоторой окрестности 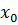 выполнено неравенство
выполнено неравенство  (рис. 43).
(рис. 43).
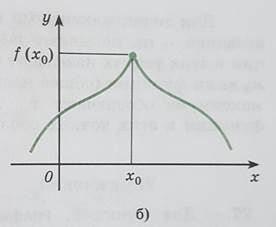


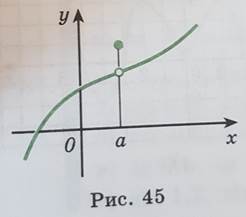 По определению значения функции f в точке максимума
По определению значения функции f в точке максимума 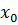 является наибольшим среди значений функции из некоторой окрестности этой точки, поэтому график функции в окрестности
является наибольшим среди значений функции из некоторой окрестности этой точки, поэтому график функции в окрестности 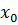 , как правило, имеет вид гладкого «холма» (рис. 43, а и рис. 44- точки
, как правило, имеет вид гладкого «холма» (рис. 43, а и рис. 44- точки  ) или заостренного «пика» (рис. 43, б). В окрестности точки минимума графики, как правило, изображаются в виде «впадины», тоже или гладкой (рис. 42, a- точка
) или заостренного «пика» (рис. 43, б). В окрестности точки минимума графики, как правило, изображаются в виде «впадины», тоже или гладкой (рис. 42, a- точка 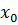 , рис. 44
, рис. 44  ), или заостренной (рис. 42, a- точка
), или заостренной (рис. 42, a- точка 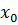 и рис. 44- точка
и рис. 44- точка  ).
).
Другие примеры поведения графиков функции в точках максимума или минимума приведены на рисунках 45 (a- точка максимума), 46 (a-точка минимума) и 47 (здесь каждая точка промежутка (-1:0) является как точкой минимума, так и точкой максимума).

 Для точек максимума и минимума функции принято общее название- их называют точками экстремума. Значение функции в этих точках называют соответственно максимумами и минимума функции (общее название- экстремум функции). Точки максимума обозначают
Для точек максимума и минимума функции принято общее название- их называют точками экстремума. Значение функции в этих точках называют соответственно максимумами и минимума функции (общее название- экстремум функции). Точки максимума обозначают  , а точки минимума
, а точки минимума  . Значения функции в этих точках обозначаются соответственно
. Значения функции в этих точках обозначаются соответственно 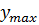 и
и  .
.
Теорема Ферма

 Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции. Эти точки играют важную роль при построении графика функции, поскольку только они могут быть точками экстремума функции (рис. 103 и 104). Сформулируем соответствующее утверждение, его называют теоремой Ферма (в честь французского математика Пьера Ферма).
Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками этой функции. Эти точки играют важную роль при построении графика функции, поскольку только они могут быть точками экстремума функции (рис. 103 и 104). Сформулируем соответствующее утверждение, его называют теоремой Ферма (в честь французского математика Пьера Ферма).
Необходимое условие экстремума.
Если точка 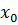 является точкой экстремума функции f и в этой точке существует производная
является точкой экстремума функции f и в этой точке существует производная  , то она равна нулю:
, то она равна нулю: 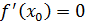 .
.
Рассмотри случай  По определению производной отношение
По определению производной отношение  при
при  стремится к положительному числу
стремится к положительному числу  , а следовательно, и само будет положительно при всех x, достаточно близких к
, а следовательно, и само будет положительно при всех x, достаточно близких к 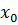 . Для таких x
. Для таких x
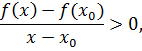
и, значит,  для всех
для всех  из некоторой окрестности точки
из некоторой окрестности точки 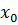 . Поэтому
. Поэтому 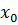 не является точкой максимума.
не является точкой максимума.
Если же  , то
, то  , и, следовательно,
, и, следовательно, 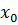 не может быть и точкой минимума f.
не может быть и точкой минимума f.
Случай  разбирается аналогично.
разбирается аналогично.
 Важно отметить, что теорема Ферма есть лишь необходимое условие экстремума: из того, что производная в точке
Важно отметить, что теорема Ферма есть лишь необходимое условие экстремума: из того, что производная в точке 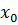 обращается в нуль, не обязательно следует, что в этой точке функция имеет экстремум. Например, производная функции
обращается в нуль, не обязательно следует, что в этой точке функция имеет экстремум. Например, производная функции  обращается в нуль в точке 0, но экстремума в этой точке функция не имеет (рис. 105).
обращается в нуль в точке 0, но экстремума в этой точке функция не имеет (рис. 105).
До сих пор мы рассматривали критические точки, в которых производная равна нулю. Рассмотрим теперь критические точки, в которых производная не существует. (Отметим, что, например, точка 0 для функции  не является критической: в ней производная не существует, но она не внутренняя точка области определения.) В этих точках функция также может иметь или не иметь экстремум.
не является критической: в ней производная не существует, но она не внутренняя точка области определения.) В этих точках функция также может иметь или не иметь экстремум.