Натуральное исчисление высказываний: правила вывода, понятия вывода, доказательства, теоремы.
Исчисление – формальная система, предназначенная для выявления корректности рассуждения на основе оперирования только синтаксическими отношениями между знаками. Доказательство в исчисления выполняется только средствами формального языка, без интерпретаций знаков.
Типы исчислений:
1. Аксиоматические. Исходные дедуктивные постулаты – аксиомы и правила вывода.
2. Натуральные исчисления (естественные) Их задача – моделировать естественные способы рассуждения, делая их корректными. Процедура поиска вывода в них проще чем в аксиоматических исчислениях. Формальные отличия от аксиоматических исчислений – нет аксиом. В качестве дедуктивных постулатов только правила вывода.
Алгоритм создания исчисления:
1) Задается формальный язык
2) Задаются начальные постулаты
3) Задаются принципы и определения вывода
4) Задаются принципы и определения доказательства
5) Определяется отношение выводимости
6) Выявляется класс теорем (доказуемых формул)
Построение классического исчисления высказываний:
1) Использующийся формальный язык – язык классической логики высказываний
2) Дедуктивные постулаты – правила перехода
Правила перехода бывают двух видов
Прямые – правила позволяющие переходить от одной или нескольких формул определенного типа к формулам определенного типа
А1,А2,…,Аn ├ В1,В2,…,Вn
Непрямые – от утверждения о выводимости перейти к утверждения другой выводимости
Г, А ├ В
Г ├ А  В
В
В классическом исчислении высказываний используются только прямые переходы:
А, В -введение А&ВА&В -исключение
А&В конъюнкции А В конъюнкции
А В -введение А 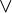 В,
В,  А -исключение
А -исключение
А 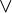 В А
В А 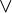 В дизъюнкции В дизъюнкции
В дизъюнкции В дизъюнкции
В -введение А  В, А -исключение
В, А -исключение
С  В импликации В импликации
В импликации В импликации
В,  В -введение
В -введение 
 А -исключение
А -исключение
 С отрицания А отрицания
С отрицания А отрицания
где С – последнее из неисключенных допущений
Особенности: При применении правил введения импликации и отрицания все формулы вывода, начиная c последнего неисключенного допущения, и вплоть до результата применения этих правил, считаются исключенными из дальнейшего построения вывода (к ним запрещается далее применять правила вывода).
3) Выводы
Вывод из множества допущений Г – это непустая конечная последовательность формул, акая что каждая формула этой последовательности есть либо допущение (посылка) из Г, либо любая формула, принятая в качестве дополнительного допущения; либо формула, полученная из предыдущих по одному из правил вывода.
Вывод формулы А из Г – вывод из Г, последняя формула которого совпадает с А
4) Доказательства
Доказательство формулы А – вывод формулы А из пустого множества неисключенных допущений.
5) Выводимость
Формула А выводима из Г, если существует вывод из Г, последняя формула которого совпадает с А
6) Теоремы
Формула А называется теоремой, если ее возможно доказать в классическом исчислении высказываний
Эвристические приемы поиска вывода в натуральном исчислении высказываний.
Эвристики – подсказки, советы по выбору принципов рассуждения при поиске вывода
Если требуется построить вывод А1,А2,…,Аn ├ В, то стратегия в общем виде такова:
Допущения – А1,А2,…,Аn
Цель – В
В случае, если напрямую В получить нельзя, надо посмотреть на структуры формулы В. Варианты:
- импликативная формула С
 В. В этом случае прямой вывод:
В. В этом случае прямой вывод:
Допущения – антецедент С
Цель – консеквент В
По правилу введения  получаем С
получаем С  В
В
- формула с отрицанием
 С. В этом случае док-во от противного:
С. В этом случае док-во от противного:
Допущения – С
Цель – противоречие В и  В
В
По правилу введения  получаем
получаем  С
С
Вспомогательные операции. Применяются только после 1 и 2 эвристик:
- Если имеется дизъюнктивная формула А
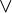 В или отрицание дизъюнкции
В или отрицание дизъюнкции  (А
(А 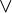 В)
В)
Допущения –  А (в первом случае) или А (во втором случае)
А (в первом случае) или А (во втором случае)
Цель в первом случае – В
Цель во втором случае – противоречие путем введения 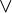 к А
к А
В целом, при рассуждении от противного необходимо стремиться к получению противоречия до тех пор, пока не будет удалена посылка, с которой мы начали это рассуждение.
- Если в выводе имеетсяимпликативная формула А
 В
В
Допущения -  А
А
Цель – противоречие
После получения противоречия мы получаем формулу 
 А, снимая отрицание получаем А, после чего по исключению
А, снимая отрицание получаем А, после чего по исключению  получаем В
получаем В
3. Классическая логика предикатов: язык, интерпретация нелогических символов, понятие модели, правила приписывания значений термам.
Язык классической логики предикатов служит для выражения логических форм с учетом внутренней структуры простых высказываний. Выражения языка, с точки зрения логики предикатов, трактуются функционально, то есть как знаки функций или аргументы функций
имена – знаки аргументов функций
предикаторы – знаки самих функций
предметные функторы – знаки предметных функций
логические связки – знаки истинностно-истинных функций
Полное название: Классическая односортная логика предикатов первого порядка.
Первого порядка
Поскольку переменные вводятся только для предметов (высший порядок – если переменные вводятся не только для предметов, но и для свойств)
Односортная
Поскольку одна и та же область интерпретации -  x
x  yR(x,y) (В многосортной каждой переменной разрешается сопоставить свою область интерпретации –
yR(x,y) (В многосортной каждой переменной разрешается сопоставить свою область интерпретации –
 x (S(x) >
x (S(x) >  y(P(y) & R (x,y)).
y(P(y) & R (x,y)).
Классическая по принципам:
1. Двузначность. Каждая формула может принять ровно одно из двух значений – И или Л.
2. Экстенсиональность. Значение сложного выражения зависит только от значения входящих в него частей.
3. Постулат о непустоте предметной области.
Язык логики предикатов:
1)Алфавит
Нелогические символы
Предметные (индивидные) константы – a, b, c,…
Предикаторные константы – Pn,Qn,Rn,… (n – местность предикатора)
Предметно-функциональные константы – fn,gn,hn,… (n – местность функтора)
Предметные переменные – x, y, z,...
Логические символы
Пропозициональные связки – выражают логические функции
& – конъюнкция, 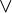 – дизъюнкция,
– дизъюнкция,  – отрицание,
– отрицание,  – импликация
– импликация
Кванторы – выражают количественные соотношения
 – общности,
– общности,  – существования
– существования
Технические символы – () ,
2)Правила образования
Термы – аналог имен
Всякая предметная переменная является термом
Всякая предметная константа является термом
Если fn – n -местная предметная константа, а t1,t2,…,tn – термы,
то fn(t1,t2,…,tn) – терм
Ни что иное не является термом
Формулы – аналог предложений
Если Pn – n-местная предикаторная константа, а t1,t2,…,tn – термы,
то Pn (t1,t2,…,tn) – формула
Если А – формула, то  А – тоже формула
А – тоже формула
Если А и В формулы, то
(А 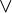 В) – формула, (А
В) – формула, (А  В) – формула, (А&В) – формула
В) – формула, (А&В) – формула
Если А – формула, а х – предметная переменная, то
 хА - формула
хА - формула
 хА - формула
хА - формула
Ни что иное не является формулой
Понятия:
1. Вхождение α в формулу А.
 xP(x,y,x) – 3 вхождения переменной х в формулу, одно вхождение переменной у
xP(x,y,x) – 3 вхождения переменной х в формулу, одно вхождение переменной у
2. Область действия квантора.
 αA,
αA,  αA – А находится в области действия квантора
αA – А находится в области действия квантора
3. Связанное/свободное вхождение.
Вхождение α называется связанным, если и только если это вхождение α непосредственно следует за квантором или находится в области действия квантора по переменной α.
Вхождение α называется свободным, если и только если это вхождение не следует за квантором и не находится в области действия никакого квантора по переменной α.
4. Свободная/связанная переменная
Переменная свободна в формуле А, если и только если существует свободное вхождение α в А.
Переменная связана в формуле А, если и только если существует связанное вхождение α в А.
Пример:  x(
x( yP(x,y,z)
yP(x,y,z) 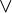 R(x,y,z))
R(x,y,z))
х - связанная, y - связанная и свободная, z - свободная
5. Правильная подстановка терма. А (α /t)
Подстановка терма t в формулу А называется правильной если и только если:
Замещаются все свободные вхождения α в А.
Ни одно из замещаемых вхождений не находится в формуле А в
области действия какого-нибудь квантора по переменной входящей в терм t.
Замкнутый терм – не содержит переменных
Замкнутая формула – не содержит свободных переменных
Интерпретация нелогических символов:
U (универсум рассмотрения) – непустое множество предметов, которые могут обозначаться нелогическими символами. Интерпретация нелогических символов будет связываться (релятивизироваться) с выбранным универсумом. U= 
Классы нелогических символов:
- константы (предметные, предикаторные, предметно-функциональные)
- предметные переменные (равны типу значений предметным константам)
I (интерпретационная функция) – функция приписывания значения константе с учетом выбранного U < U, I > - модель языка
Интерпретация констант:
Предметные константы – аналоги имен. Значение имени – отдельный предмет, взятый из U. Функция I каждой предметной константе сопоставляет элемент множества U
I: I (k) 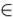 U
U
Предикаторные константы – аналоги предикаторов, которые в качестве значений имеют свойства или отношения, либо являются знаками множеств предметов, обладающих этими свойствами или кортежей предметов, находящихся в этих отношениях. Таким образом, значением предикаторной константы является некоторое подмножество U
I: I (Пn)  Un
Un
Предметно-функциональные константы – аналоги предметных функторов. Значения – предметно-предметные функции, определенные на множестве U
I: I(Фn) - функция вида Un → U.
Интерпретация предметных переменных:
Функция φ предметным переменным сопоставляет произвольные объекты множества U того же самого типа, что и константам.
I: φ (α) 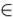 U
U
Выбрав U и I – задаем модель языка m = <U,I>, где
U – произвольное непустое множество
I – семантическая функция приписывающая значение константам языка.
Модель - возможная реализация языка.
Правила приписывания значений термам:
Значения термов – некоторые элементы из универсума.
Три типа термов:
α – предметные переменные
k – предметные константы
Фn (t1,t2,…,tn) – сложные функциональные термы
Значение терма t в модели m при приписывании значений φ:
Краткая запись - |t| m φ или просто |t| φ
Для предметных переменных
| α | φ = φ (α)
Для предметных констант
| k | φ = I (k)
Для сложных термов
| Фn (t1,t2,…,tn) | φ = [ I(Ф)] (| t1| φ,| t2| φ,....| tn | φ)
4. Классическая логика предикатов: правила приписывания значений формулам, понятия общезначимой и выполнимой формул, определение основных логических отношений между формулами.
Значения, которые могут принимать формулы при интерпретации – истина (И) и ложь (Л)
Значения формул при интерпретации:
Атомарные формулы принимают значение И в том случае, если элементы множества U, знаками которых являются термы t1,t2,…,tn, входящие в формулу, являются и элементами подмножества U, обозначенного предикатором Пn
| Пn (t1,t2,…,tn)| φ = И↔ <| t1| φ,| t2| φ,....| tn | φ >  I (Пn)
I (Пn)
| Пn (t1,t2,…,tn)| φ = Л ↔ <| t1| φ,| t2| φ,....| tn | φ >  I (Пn)
I (Пn)
Значение формулы  А противоположно значению формулы А
А противоположно значению формулы А
|  А| φ = И ↔ |А| φ = Л
А| φ = И ↔ |А| φ = Л
|  А| φ = Л ↔ |А| φ = И
А| φ = Л ↔ |А| φ = И
Значение формулы А & В равно И в том случае, если значение обоих формул, входящих в конъюнкцию, равно И, и равно Л во всех остальных случаях
|А & В| φ = И ↔ |А| φ = И &˚ |В| φ =И
|А & В| φ = Л ↔ |А| φ = Л 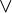 ˚ |В| φ =Л
˚ |В| φ =Л
Значение формулы А 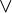 В равно И в том случае, если значение хоть одной из формул, входящих в нее, равно И
В равно И в том случае, если значение хоть одной из формул, входящих в нее, равно И
|А 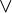 В|φ = И ↔ |А|φ = И
В|φ = И ↔ |А|φ = И 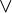 ˚ |В|φ=И
˚ |В|φ=И
|А 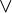 В|φ = Л ↔ |А|φ = Л &˚ |В|φ=Л
В|φ = Л ↔ |А|φ = Л &˚ |В|φ=Л
Значение формулы А  В равно И, если значение формулы антецедента равно Л или значение консеквентна равно И
В равно И, если значение формулы антецедента равно Л или значение консеквентна равно И
|А  В|φ = И ↔ |А|φ = Л
В|φ = И ↔ |А|φ = Л 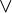 ˚ |В|φ=И
˚ |В|φ=И
|А  В| φ = Л ↔ |А|φ = И &˚ |В|φ=Л
В| φ = Л ↔ |А|φ = И &˚ |В|φ=Л
Значение формулы  α А равно И, если значение ЛЮБОЙ функции ψ, отличающейся от φ не более, чем приписыванием значения переменной α, равно И
α А равно И, если значение ЛЮБОЙ функции ψ, отличающейся от φ не более, чем приписыванием значения переменной α, равно И
|  α А|φ = И ↔
α А|φ = И ↔  ˚ψ (ψ= α φ
˚ψ (ψ= α φ  ˚ |A|ψ = И) ψ= α φ – приписывание ψ значения
˚ |A|ψ = И) ψ= α φ – приписывание ψ значения
|  α А|φ = Л ↔
α А|φ = Л ↔  ˚ψ (ψ= α φ &˚ |A|ψ = Л) отличного от φ не более, чем на α
˚ψ (ψ= α φ &˚ |A|ψ = Л) отличного от φ не более, чем на α
Значение формулы Е α А, если значение ХОТЬ ОДНОЙ функции ψ, отличающейся от φ не более, чем приписыванием значения переменной α, равно И
|  α А|φ = И ↔
α А|φ = И ↔  ˚ψ (ψ= α φ &˚ |A|ψ = И) ψ= α φ – приписывание ψ значения
˚ψ (ψ= α φ &˚ |A|ψ = И) ψ= α φ – приписывание ψ значения
|  α А|φ = Л ↔
α А|φ = Л ↔  ˚ψ (ψ= α φ
˚ψ (ψ= α φ  ˚ |A|ψ = Л) отличного от φ не более, чем на α
˚ |A|ψ = Л) отличного от φ не более, чем на α
Виды формул:
Закон (общезначимая формула) – это формула, принимающая значение И во всех моделях и при любых приписываемых значениях предметным переменным
╞ A ≡ Df  ˚U
˚U  ˚I
˚I  ˚φ |A|φ <U,I> = И
˚φ |A|φ <U,I> = И
Выполнимая формула – принимающая значение И в некоторых моделях и при некоторых приписываниях значений предметным переменным
Формула А выполнима ≡ Df  ˚U
˚U  ˚I
˚I  ˚φ |A|φ <U,I>= И
˚φ |A|φ <U,I>= И
Невыполнимая формула – это формула, принимающая значение Л во всех моделях и при любых приписываемых значениях предметным переменным
Формула А невыполнима ≡Df  ˚U
˚U  ˚I
˚I  ˚φ |A|φ <U,I> = Л
˚φ |A|φ <U,I> = Л
Опровержимая формула - принимающая значение Л в некоторых моделях и при некоторых приписываниях значений предметным переменным
Формула А опровержима ≡ Df  ˚U
˚U  ˚I
˚I  ˚φ |A|φ <U,I>= Л
˚φ |A|φ <U,I>= Л
Формула А значима (истинна) в модели <U,I> ≡Df  ˚φ |A|φ<U,I> = И
˚φ |A|φ<U,I> = И
Формула А общезначима на множестве U (U общезначима) ≡Df  ˚I
˚I  ˚φ |A|φ<U,I> = И
˚φ |A|φ<U,I> = И
Логические отношения
Совместимость по истинности.
Формулы из Г совместимы по истинности в том случае, если существует такая модель и такое приписывание значений переменным, при котором каждая формула из Г примет значение И.
 ˚A (A
˚A (A 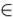 Г
Г  ˚
˚  ˚U
˚U  ˚I
˚I  ˚φ |A|φ = И)
˚φ |A|φ = И)
Совместимость по ложности
Формулы из Г совместимы по ложности в том случае, если существует такая модель и такое приписывание значений переменным, при котором каждая формула из Г примет значение Л.
 ˚A (A
˚A (A 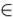 Г
Г  ˚
˚  ˚U
˚U  ˚I
˚I  ˚φ |A|φ = Л)
˚φ |A|φ = Л)
Логическое следование.
Имеется в том случае, если для всякой модели и для всякого приписывания значений переменным, при котором каждое значение из Г примет значение И, формула В тоже примет значение И.
Г ╞ B ↔  ˚U
˚U  ˚I
˚I  ˚φ (
˚φ (  ˚A (A
˚A (A 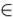 Г
Г  ˚ |A|φ = И)
˚ |A|φ = И)  ˚ |В|φ = И)
˚ |В|φ = И)
Задачи, решаемые в логике предикатов перебором моделей
-обоснование выполнимости
- обоснование опровержимости
-соместимость по истинности и по ложности
Обосновать общезначимости, невыполнимость, несовместимость по И и Л или отношение логического следования невозможно.