Пусть 
– знакоположительный ряд. Если существует 
,
то при 
ряд сходится, а при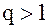 
ряд расходится.
Если 
ряд может как сходиться, так и расходиться. Выяснить это можно с помощью дополнительного исследования, например, используя признаки сравнения.
При применении радикального признака Коши бывает полезно знать, что
. (3)
Пример 7. Исследовать на сходимость ряд с помощью радикального признака Коши
| а) |  ;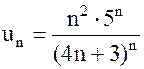
| б) |  ;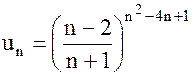
| в) |  ;
|
| г) |  ;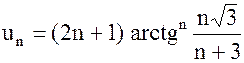
| д) |  .
|
Решение. а) Так как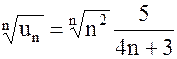 
и 
,
(см. равенство (3)), то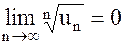 
и поэтому ряд 
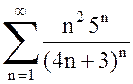сходится.
б) В этом случае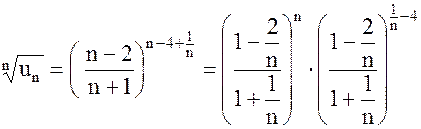 
. Так как
(см. [5]), а 
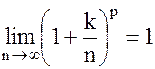, то
Это означает, что данный ряд сходится.
в) В этом случае удобно применить признак Коши, т. к.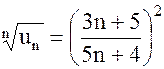 
, а предел этого выражения находится просто:
.
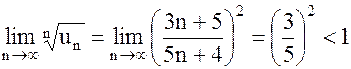Значит, ряд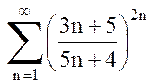 
сходится.
г) Заметим, что при 
, а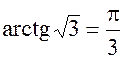 
.
Кроме того, т. к. , то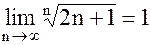 
, поэтому
и поэтому ряд расходится.
д) Так как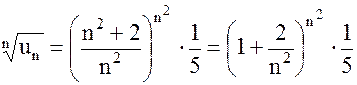 
и
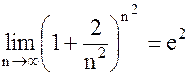(см. [5]), то 
.
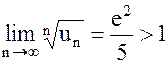Следовательно, ряд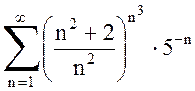 
расходится.
Признак Даламбера и радикальный признак Коши основаны, по существу, только на свойствах геометрической прогрессии. Поэтому при исследовании медленно сходящихся или медленно расходящихся рядов (прогрессии в их число не входят) эти признаки оказываются нечувствительными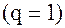 
. В таких случаях, кроме признаков сравнения, можно использовать интегральный признак Коши. Этот признак четко проводит различия между сходящимися и расходящимися рядами, даже если члены одного из них лишь незначительно отличаются от членов другого.
Интегральный признак Коши
Пусть члены знакоположительного ряда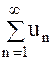 
не возрастают:
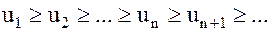. Пусть, кроме того, 
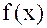– непрерывная,
невозрастающая функция, определенная для всех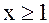 
, такая, что
. Тогда ряд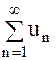 
и несобст-
венный интеграл 
сходятся или расходятся одновременно.
Пример 8. Исследовать на сходимость ряд 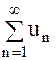с помощью интегрального признака Коши, если
| а) |  ;
| б) |  ;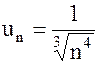
| в) |  ;
| г) |  .
|
Решение. а) 
– ряд Дирихле с 
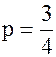. Ранее было отмечено, что этот ряд расходится. Докажем это. Рассмотрим функцию 
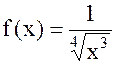. Она не-
прерывна и убывает при всех 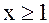. Кроме того, 
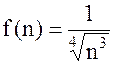, поэтому 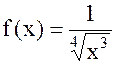удовлетворяет условиям теоремы.
Вычислим 
.
Несобственный интеграл расходится, значит, расходится и данный ряд.
б)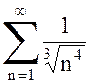 
– ряд Дирихле с 
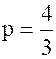. Как было отмечено, этот ряд сходится.
Чтобы убедиться в этом, применим интегральный признак Коши: ,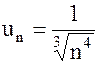
; 
.
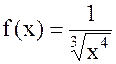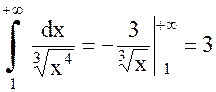Несобственный интеграл сходится, поэтому сходится и данный ряд.
в) Рассмотрим при 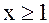функцию 
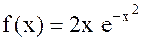. Ее производная
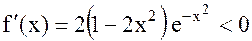при всех 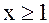. Следовательно, 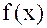убывает
и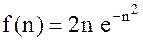 
.
.
Несобственный интеграл сходится, а потому сходится и данный ряд.
г) Функция 
непрерывна и убывает при всех 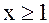. Несобственный интеграл
,
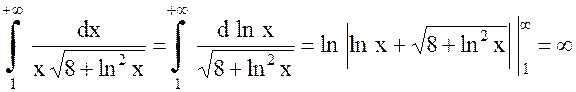т. е. расходится, значит, ряд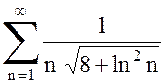 
тоже расходится.
Знакочередующиеся ряды
Определение. Ряды, члены которых имеют разные знаки, называются знакопеременными. Если члены ряда поочередно имеют то положительный, то отрицательный знаки, то ряд называется знакочередующимся.
Знакочередующиеся ряды – частный случай рядов знакопеременных.
Если 
, то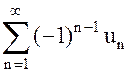 
– знакочередующийся ряд. Например, ряды
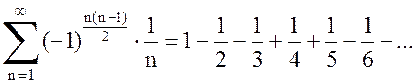
и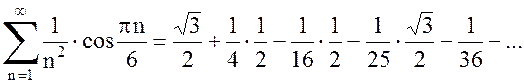 
знакопеременные, а ряды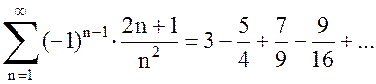 
,
,
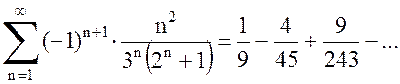и 
– знакочередующиеся.
Для знакочередующихся рядов имеет место следующий достаточный признак сходимости.
Признак Лейбница
Пусть члены знакочередующегося ряда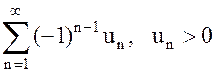 
удовлетворяют условиям:
1) 
;
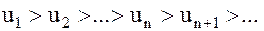2) 
.
Тогда ряд сходится, и его сумма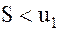 
.
Пример 9. Исследовать на сходимость ряд 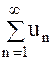, если
| а) |  ;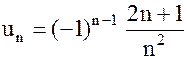
| б) |  .
|
Решение. а) Ряд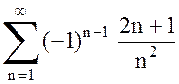 
– знакочередующийся, 
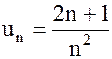. Проверим условия признака Лейбница:
1) 
;
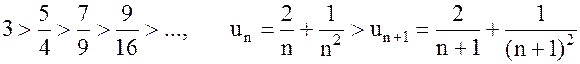2) 
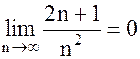(см. [5]).
Делаем вывод, что ряд сходится.
б) Ряд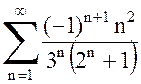 
– также знакочередующийся.
Он сходится, т. к. удовлетворяет условиям признака Лейбница:
и 1)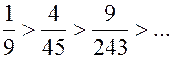 
; 2)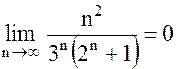 
,
потому что знаменатель этой дроби при 
растет гораздо быстрее числителя.
Для знакопеременных рядов имеет место следующий признак сходимости.