распределения. распределения.

2.2.6.3 Нормальное распределение.

Нормальное распределение играет важнейшую роль как в теоретическом, так и в практическом аспектах. В разработке этого закона и законов, связанных с ним, фундаментальные исследования выполнили П.-С. Лаплас, А. Муавр, К. Гаусс, К. Пирсон, У. Госсет и Р.Фишер. Особенно велика заслуга П.-С. Лапласа и К. Гаусса, в связи с чем, нормальное распределение часто называют распределением Лапласа-Гаусса.

Плотность вероятности нормального распределения имеет вид

f (x) = , (66)

для всех x ]-∞;∞[. В формуле (66) величины p и e – математические константы, a и b > 0 – параметры распределения, математический и вероятностный смысл которых станет понятен при детальном изучении этой кривой и получении числовых характеристик нормального закона.

Исследования формулы (66) показывают, что кривая плотности лежит над осью абсцисс, которая является асимптотой для левой и правой её ветвей. Кривая симметрична относительно ординаты x = a и имеет единственный максимум, когда x = a, что следует из уравнения производной функции плотности, приравненного к нулю:

f ΄(x) = – (x – a) ∙ b ^-3 ∙ (2p)^-1/2 ∙ exp(– (x – a)² / (2 b ²)) = 0,

и изменений знаков производной в районе точки экстремума. Кривая нормальной плотности имеет две точки перегиба, абсциссы которых равны, соответственно, (a – b) и (a + b). Итак, математический смысл параметров a и b установлен: a – абсцисса точки максимума, а b – расстояние от точки a до абсциссы точки перегиба.

Перейдем к исследованию вероятностных характеристик нормального закона Лапласа-Гаусса.

Дано: f (x) = для всех x ]-∞;∞[.

Найти: 1) E (X) –? 2) Mo(X) –? 3) Me(X) –? 4) D (X) –? 5) s _X –?

6) ϑ _X –? 7) F (x) –? 8) P (x ₁< X < x ₂) –?

Решение:

1) Согласно определению математического ожидания (51) для непрерывной случайной величины имеем:

E (X) = = .

Произведем замену переменных:

t = (x – a) / b. (67)

Такая замена означает перенос начала оси абсцисс в точку a и принятие параметра b за единицу длины новой оси абсцисс. Из (67) следует, что

t ] –∞; ∞ [; x = bt + a; dx = b · dt.

Продолжим нахождение математического ожидания нормальной случайной величины, выполнив замену переменных (67):

E (X) = 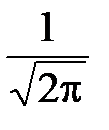^- dt = (J ₁ + a · J ₂). (68)

Найдём интегралы, входящие в (68):

J ₁ = b = – b = – b ( – ) =0;

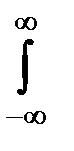J ₂ = e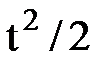^– = – (интеграл Пуассона).

Окончательно имеем:

E (X) = = a. (69)

2) В соответствие с (55) и установленными математическим и вероятностным смыслами параметра a мода нормальной случайной величины совпадает с её математическим ожиданием:

Mo(X) = arg(f (x)=max) = a = E (X). (70)

3) Ордината, проходящая через медиану, делит площадь под кривой плотности на две равные половины (2.2.5.1). Поскольку для симметричной нормальной кривой основанием этой ординаты является точка a, то

Me(X) = a = E (X) = Mo(X). (71)

4) Для нахождения дисперсии нормального распределения удобно воспользоваться рекуррентной формулой его центральных моментов [8]:

m _r = m _{r -2} ∙ (r – 1) ∙ b ². (72)

Из Таблицы 2.1 (параграф 2.2.5.2) имеем: m₀ 1. Следовательно,

D (X) = s _X ² = m₂ = m₀ ∙ (2 – 1) ∙ b ² = b ². (73)

5) Искомый стандарт нормального распределения раскрывает вероятностный смысл параметра b:

s _X = + = b. (74)

Учитывая вероятностный смысл параметров a и b, замену переменных (67) можно представить как функцию числовых характеристик:

t = (x – a) / b = (x – E (X)) / σ _X. (75)

6) Среднее отклонение нормального распределения ϑ _X определяется общим правилом (64) и плотностью (66):

ϑ _X = t₁ = = .

Производя уже применявшуюся замену переменных (59) и учитывая симметричность кривой нормальной плотности, получаем:

ϑ _X = b 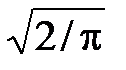= – b =

= – b ( – ) = – b ·(0 – 1) →

ϑ _X = b = σ _X ≈ (4 / 5)·σ _X. (76)

7) Нормальная ФР F (x) связана с ее плотностью соотношением (50):

F (x) = = . (77)

Интеграл (77) не выражается через элементарные функции, вследствие чего возникает необходимость его табулирования. Однако, для формулы (77) требуется таблица с тремя входами: a, b и x, что практически не приемлемо. Выход из этой ситуации осуществляется путем нормирования распределения Гаусса по формуле (75), так как СВ t имеет нулевое среднее и единичный стандарт, что обусловлено ограничением b > 0:

E (t) = E ((x – a) / b) = (a – a) / b ≡ 0,

D (t) = D ((x – a) / b) = D (x / b – a / b) = D (x / b) = 1 / b ² ∙ D (x) = b ² / b ² ≡ 1.

Стандартная функция распределения Гаусса имеет вид:

F (t) = . (78)

Таблица значений стандартной нормальной функции (78) помещена в Приложении Д, а в Приложении Г помещена таблица стандартной нормальной плотности:

f (t) = . (79)

Стандартная нормальная функция (78) обладает свойством:

F (– t) + F (t) = 1. (80)

8) Вероятность попадания нормальной СВ на интервал ] x ₁; x ₂[ вычисляется с помощью стандартной нормальной ФР (78) после нормирования границ этого интервала по формуле (75):

P (x ₁< X < x ₂) = F (t ₂) – F (t ₁). # (81)

В заключение отметим, что, взамен выражения плотности нормального распределения в форме (66) или (79), принята более краткая запись:

X N (a; b) или t N (0; 1). (82)

Записи (82) читаются следующим образом: первая – «случайная величина X подчиняется нормальному закону, у которого E (X) = a, а σ _X = b » и вторая – «стандартная нормальная случайная величина t имеет нулевое математическое ожидание и единичный стандарт».

На рисунках (Рис.21 и 2 2) представлены графики плотности нормального распределения и функции этого же закона.

f (x)

X

a

a+b

f max=1/(b )

f (t)

+1

-1

a-b

T

Рис. 2.21 Плотность нормального распределения.

F (x)

1.0

X

x 1

x 2

F 1

F 2

P (a ≤ X < b)= F 2- F 1

t 1

t 2

T

F (t)

a

Рис. 2.22 Функция нормального распределения.

Распределение Гаусса играло и продолжает играть свою роль при моделировании ошибок измерений. Кроме того, нормальное распределение и связанные с ним законы широко используются при построении допустимых границ ожидаемых результатов измерений и вычислений.

Задача 2.12. Какова вероятность того, что нормальная случайная величина, имеющая математическое ожидание, равное 8 -и и стандарт, равный 3 -м, попадет в интервал ] 2; 14 [?

Дано: X N (8; 3);

Найти: P (x ₁ = 2 < X < x ₂ = 14) –?

Решение: В соответствие с формулами (81) и (75) получаем такие соотношения:

P(2 < X < 14) = F (t ₂) – F (t ₁) = F ((14 – 8) / 3 – F ((2 – 8) / 3 = F (2) – F (– 2).

С учетом свойства (80) стандартной нормальной функции распределения и равенства t ₂ = 2= – t ₁ = 2, последнее выражение принимает вид:

P (2 < X < 14) = 2 F (2) – 1 = P (| X – E (X)| < 2σ _X).

По таблице, помещенной в Приложении Д, находим F (2) = 0,977. Окончательно определяем искомую вероятность:

P (2 < X < 14) = 2 · 0,977 – 1 = 0,954.

Иными словами, вероятность того, что нормальная случайная величина уклонится от своего центра рассеивания по модулю больше, чем на два стандарта, равна 0,046, или 4,6%. #

Задача 2.13 Для X N (8; 3) построить интервал (x ₁, x ₂) = I _γ, длина которого равна 2ε, симметричный относительно центра рассеивания. Вероятность g попадания X в этот интервал должна равняться 0,683.

Дано: E (X) = 8; s _X = 3; g = 0,683; I _γ = 2ε.

Найти: x ₁ и x ₂, если P (x ₁< X < x ₂) = g; E (X) – x ₁ = x ₂ – E (X) = ε.

Решение: Условие симметричности интервала относительно центра рассеивания E (X) позволяет выстроить цепочку преобразований, подобных тем, которые были выполнены в предыдущем примере:

γ = P(x ₁ < X < x ₂) = F (t ₂) – F (t ₁) = 0,683;

однако из (75) следует, что

t ₂ = (x ₂ – E (X)) / σ _X = ε / σ _X;

t ₁ = (x ₁ – E (X)) / σ _X = – ε / σ _X;

t ₂ = – t ₁ = t.

Теперь

γ = P (x ₁ < X < x ₂) = 2 F (t) – 1.

С другой стороны, путём обратного интерполирования по таблице стандартной нормальной функции (Приложение Д), находим аргумент t:

t = arg(F = (1 + γ / 2)) = arg(F = (0.842)) = 1.

Поскольку

t = ε / σ _X,

то e = t ∙ σ _X = 3, и можно вычислить границы интервала в системе координат исходной переменной X:

x ₁ = E (X) – ε = 8 – 3 = 5,

x ₂ = E (X) +ε = 8 + 3 = 11. #