Минором mij некоторого элемента aij определителя n–го порядка называется определитель (n – 1)-го порядка, полученный из исходного определителя путем вычеркивания i-й строки и j-го столбца, на пересечениях которых находится выбранный элемент.
Например, минором элемента a11 определителя третьего порядка является  .
.
Алгебраическим дополнением называется Aij = (– 1) i+j mij. Если сумма индексов алгебраического дополнения i + j четное число, то алгебраические дополнения и миноры совпадают: Aij = mij, а если – нечетное число, то они отличаются знаком: Aij = – mij.
Свойства определителей
1. Если какой-то ряд состоит из одних нулей, то определитель равен 0.
2. Определитель не изменится, если его строки заменить столбцами, и наоборот.
3. При перестановке двух параллельных рядов определитель меняет знак.
4. Определитель, имеющий два одинаковых ряда, равен нулю.
5. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
6. Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух определителей, с соответствующими слагаемыми этой суммы.
7. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.
8. Определитель равен сумме произведений элементам некоторого ряда на соответствующие им алгебраические дополнения.
Например, определитель третьего порядка равен:
detA = a11A11 + a12A12 + a13A13 = a11m11 – a12m12 + a13m13. (3)
@ Задача 3. Найти  .
.
Решение: Определитель найдем, применяя формулу (3):

Ранг матрицы
Наибольший порядок отличных от нуля детерминантов (миноров) прямоугольной матрицы m ´ n, называется рангом матрицы r, причем r £ min(m, n). Для квадратной матрицы ранг r £ n.
Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров.
@ Задача 4. Найти ранг матрицы  размерности 3´4.
размерности 3´4.
Решение: Ранг матрицы r £ min(3, 4) = 3. Все детерминанты третьего порядка равны нулю, так как две их строки (вторая и третья) одинаковые (отличаются на постоянный множитель). Отличны от нуля только детерминанты второго порядка, поэтому r = 2.
§ 1.4. Обратная матрица
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля: detA ¹ 0. В противном случае матрица называется вырожденной.
Матрица A- 1 называется обратной матрице А, если выполняется условие
A- 1 A = AA- 1 = E.
Только у невырожденных квадратных матриц есть обратные матрицы.
Обратная матрица вычисляется по формуле (detA ¹ 0):
 .
.
Для матрицы A второго порядка обратная матрица равна:
 .
.
@ Задача 1. Найти A- 1, если  .
.
Решение: 1. Находим определитель матрицы:
 .
.
2. Находим обратную матрицу:
 .
.
@ Задача 2. Найти A- 1, если  .
.
Решение: 1. Находим определитель матрицы:
 .
.
2. Вычисляем алгебраические дополнения:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
3. Находим обратную матрицу:
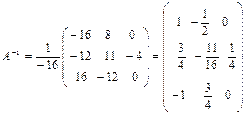 .
.