Обратные тригонометрические функции, их свойства и графики.

Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки "арк" обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.

Функция арксинус y = arcsin(x).

Изобразим график функции арксинус:

Свойства функции арксинус y = arcsin(x).

· Областью определения функции арксинус является интервал от минус единицы до единицы включительно: .

· Область значений функции y = arcsin(x): .

· Функция арксинус - нечетная, так как .

· Функция y = arcsin(x) возрастает на всей области определения, то есть, при .

· Функция вогнутая при , выпуклая при .

· Точка перегиба (0; 0), она же ноль функции.

· Асимптот нет.

К началу страницы

Функция арккосинус y = arccos(x).

График функции арккосинус имеет вид:

Свойства функции арккосинус y = arccos(x).

· Область определения функции арккосинус: .

· Область значений функции y = arccos(x): .

· Функция не является ни четной ни нечетной, то есть, она общего вида.

· Функция арккосинус убывает на всей области определения, то есть, при .

· Функция вогнутая при , выпуклая при .

· Точка перегиба .

· Асимптот нет.

К началу страницы

Функция арктангенс y = arctg(x).

График функции арктангенс имеет вид:

Свойства функции арктангенс y = arctg(x).

· Область определения функции y = arctg(x): .

· Область значений функции арктангенс: .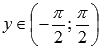

· Функция арктангенс - нечетная, так как .

· Функция возрастает на всей области определения, то есть, при .

· Функция арктангенс вогнутая при , выпуклая при .

· Точка перегиба (0; 0), она же ноль функции.

· Горизонтальными асимптотами являются прямые при и при . На чертеже они показаны зеленым цветом.

К началу страницы

Функция арккотангенс y = arcctg(x).

Изобразим график функции арккотангенс:

Свойства функции арккотангенс y = arcctg(x).

· Областью определения функции арккотангенс является все множество действительных чисел: .

· Область значений функции y = arcctg(x): .

· Функция арккотангенс не является ни четной ни нечетной, то есть, она общего вида.

· Функция убывает на всей области определения, то есть, при .

· Функция вогнутая при , выпуклая при .

· Точка перегиба .

· Горизонтальными асимптотами являются прямые 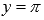при (на чертеже показана зеленым цветом) и y = 0 при .

· Геометрия окружности и круга

· Геометрическим местом точек называется совокупность всех точек, удовлетворяющих заданным условиям. Окружность есть геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). Равные отрезки, соединяющие центр с точками окружности, называются радиусами и обозначаются буквами r или R. Дуга — это часть окружности. Секущая — это прямая проходящая через две точки окружности. Хорда — это отрезок секущей, лежащий внутри окружности. С приближением к центру хорда увеличивается.

Окружность и радиус

Окружность и дуга окружности

Окружность и секущая

· Диаметр — это хорда проходящая через центр окружности (обозначается d или D). Диаметр равен двум радиусам:

· Круг есть часть плоскости, лежащая внутри окружности. Касательная — это прямая пересекающаяся окружность только в одной точке. Касательная это выродившаяся секущая. Касательная к окружности перпендикулярна радиусу проведенному в точку касания. Из одной точки вне круга можно провести к окружности две касательные. Их длины будут равны.

Окружность и касательная

Сегмент окружности

Сектор окружности

· Сегмент — это часть круга, ограниченная дугой и стягивающей ее хордой. Стрелка дуги — это перпендикуляр восстановленный из середины хорды до пересечения с дугой. Высота сегмента — это длина стрелки дуги. Сектор — это часть круга, ограниченная дугой и двумя радиусами, проведенными к концам дуги. Квадрант — это сектор, отсекаемый радиусами, образующими угол 90°.

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.

· Окружность — линия, ограничивающая круг.

· Дуга — часть окружности.

· Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.

· Хорда — отрезок, соединяющий две точки окружности.

· Сегмент — часть круга, ограниченная хордой и дугой.

· Сектор — часть круга, ограниченная двумя радиусами и дугой.

Интересующие нас величины и их обозначения:

· R — радиус круга (здесь «радиус» — это уже не отрезок, а его длина);

· D — диаметр круга — двойной радиус;

· C — длина окружности;

· L — длина дуги;

· X — длина хорды;

· H — высота сегмента;

· φ — центральный угол — угол между двумя радиусами;

· — площадь круга;

· — площадь сектора;

· — площадь сегмента.

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

· Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.

· Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.

· Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.