Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу.
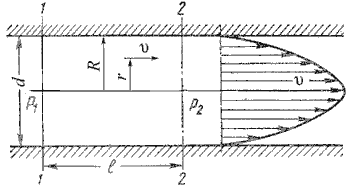
Рис. 4.3. Схема для рассмотрения ламинарного потока
Потеря давления в трубопроводе будет равна
Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:
где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:
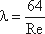
Закон Пуазёйля (иногда закон Гагена — Пуазёйля) — это физический закон установившегося течения вязкой несжимаемой жидкости в тонкой цилиндрической трубке.
где
· 
— перепад давления на концах капилляра, Па;
· 
— объёмный расход жидкости, м³/с;
· 
— радиус капилляра, м;
· 
— диаметр капилляра, м;
· 
— коэффициент динамической вязкости, Па·с;
· 
— длина капилляра, м.
Потери напора при турбулентном режиме движения жидкости. Определение коэффициента сопротивления Дарси при турбулентном режиме движения при различных числах Рейнольдса и относительной шероховатости труб (области гладкого трения, доквадротичного и квадротичного сопративления). График Никурадзе-Мурина.
Для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рис.4.4. Скорость беспорядочно колеблется около некоторого осредненного по времени значения υ оср, которое данном случае остается постоянным.
При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рис. 4.6. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.
Рис. 4.6. Модель турбулентного режима движения жидкости
Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:
Гидравлически гладкие трубы (турбулентный режим).
Гидравлически гладкие трубы – это трубы, в которых величина выступов шероховатости не влияет на характер распределения скоростей и на величину потерь напора (стеклянные, цельнотянутые трубы из цветных металлов, высококачественные бесшовные стальные трубы, то есть топливопроводы, трубы гидросистем гидроприводов).
Для развитого турбулентного течения (4000 < Re < 105) можно пользоваться формулой Блазиуса
или Конакова 
III. Доквадратичное сопротивление (турбулентный режим).
Этот режим наблюдается, когда толщина пристенного ламинарного слоя dл примерно равна величине эквивалентной равномерно-зернистой шероховатости Dэ. Значения Dэ для различных типов труб можно найти в справочной литературе.
Для этого режима 
, где d – диаметр трубы, можно применить формулу Альтшуля:
IV. Квадратичное сопротивление (режим турбулентный).
Этот режим наблюдается при Re > 500 
. Наиболее универсальна формула Прандтля-Никурадзе:
