Свойства хорд
1. 
Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.
2. Дуги, заключенные между параллельными хордами, равны.
3. Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.
Свойства окружности
1. Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
2. Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
3. Точка касания двух окружностей лежит на линии, соединяющей их центры.
Теорема о касательной и секущей
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB.
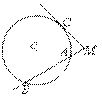
Теорема о секущих
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. MA•MB = MC•MD.
Углы в окружности
Центральным углом в окружности называется плоский угол с вершиной в ее центре.
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом. 
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Мерой дуги может служить мера соответствующего ей центрального угла.
Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Свойства углов, связанных с окружностью
1. Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°. 
2. Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
3. Вписанный угол, опирающийся на диаметр, равен 90°.
4.
5. Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Длины и площади
1. Длина окружности C радиуса R вычисляется по формуле: C = 2 
R.
2. Площадь S круга радиуса R вычисляется по формуле: S = R2.
3. Длина дуги окружности L радиуса R с центральным углом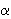 
,измеренным в радианах, 
вычисляется по формуле: L = R .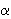
4. Площадь S сектора радиуса R с центральным углом в 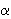радиан вычисляется по формуле: S = 
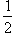R2 .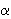
Вписанные и описанные окружности
Окружность и треугольник 
· центр вписанной окружности — точка пересечения биссектрис треугольника, ее радиус r вычисляется по формуле:
r = 
, где S — площадь треугольника, а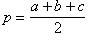 
— полупериметр;
· центр описанной окружности — точка пересечения серединных перпендикуляров, ее радиус Rвычисляется по формуле: 
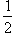
R = 
, R = 
;
;
· центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы;
· центр описанной и вписанной окружностей треугольника совпадают только в том случае, когда этот треугольник — правильный.
Окружность и четырехугольники
· около выпуклого четырехугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных 
углов равна 180°: 
+ 
= 
+ 
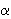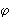= 180°;
в четырехугольник можно вписать окружность тогда и только тогда, когда у него равны суммы противоположных сторон a + c = b + d;
около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
· около трапеции можно описать окружность тогда и только тогда, когда эта трапеция — равнобедренная; центр окружности лежит на пересечении оси симметрии трапеции с серединным перпендикуляром к боковой стороне;
· в параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
Треугольники