Свойства медиан треугольника

1. Медиана разбивает треугольник на два треугольника одинаковой площади.

2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.

3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.

Свойства биссектрис треугольника

1. Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.

2. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегажащим сторонам: .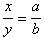

3. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.

Свойства высот треугольника

1. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.

2. В остроугольном треугольнике две его высоты отсекают от него подобные 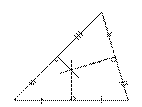треугольники.

Свойства серединных перпендикуляров треугольника

1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

2. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Свойство средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Подобие треугольников

Два треугольника подобны, если выполняется одно из следующих условий, называемых признаками подобия:

· два угла одного треугольника равны двум углам другого треугольника;

· две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами, равны;

· три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника.

В подобных треугольниках соответствующие линии (высоты, медианы, биссектрисы и т. п.) пропорциональны.

Теорема синусов

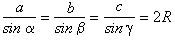
Теорема косинусов

a² = b² + c² - 2 bc cos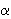

Формулы площади треугольника

1. Произвольный треугольник

a, b, c — стороны; 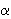— угол между сторонами a и b; 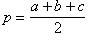— полупериметр; R — радиус описанной окружности; r — радиус вписанной окружности; S — площадь; h_a — высота, проведенная к 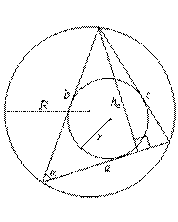стороне a.

S = 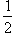ah_a

S = 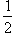ab sin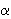

S = pr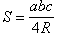

2. Прямоугольный треугольник

a, b — катеты; c — гипотенуза; h_c — высота, проведенная к стороне c.

S = 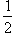ch_c S = 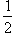ab

3. Равносторонний треугольник

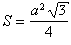
Четырехугольники

Свойства параллелограмма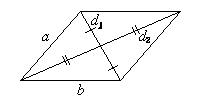

· противолежащие стороны равны;

· противоположные углы равны;

· диагонали точкой пересечения делятся пополам;

· сумма углов, прилежащих к одной стороне, равна 180°;

· сумма квадратов диагоналей равна сумме квадратов всех сторон:

d₁²+d₂²=2(a²+b²).

Четырехугольник является параллелограммом, если:

1. Две его противоположные стороны равны и параллельны.

2. Противоположные стороны попарно равны.

3. Противоположные углы попарно равны.

4. Диагонали точкой пересечения делятся пополам.

Свойства трапеции

· ее средняя линия параллельна основаниям и равна их полусумме;

· если трапеция равнобокая, то ее диагонали равны и углы при основании равны;

· если трапеция равнобокая, то около нее можно описать окружность;

· если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.

Свойства прямоугольника

· все свойства параллелограмма;

· диагонали равны.

Параллелограмм является прямоугольником, если:

1. Один из его углов прямой.

2. Его диагонали равны.

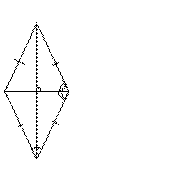
Свойства ромба

· все свойства параллелограмма;

· диагонали перпендикулярны;

· диагонали являются биссектрисами его углов.

1. Параллелограмм является ромбом, если:

2. Две его смежные стороны равны.

3. Его диагонали перпендикулярны.

4. Одна из диагоналей является биссектрисой его угла.

Свойства квадрата

· все углы квадрата прямые;

· диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

Основные формулы

1. Произвольный выпуклый четырехугольник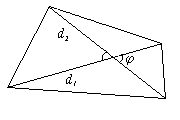
d₁, d₂ — диагонали; 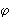— угол между ними; S — площадь.

S = 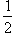d ₁ d ₂ sin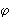

2. Параллелограмм

S = ah_a

S = ab sin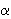

S = 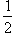d ₁ d ₂ sin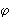

3. Трапеция

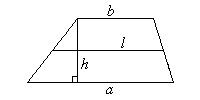
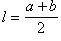
S = lh

4. Прямоугольник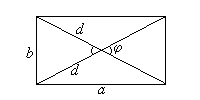

S = ab

S = 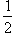d ₁ d ₂ sin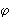

5. Ромб

S = ah_a

S = a²sin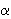

S = 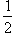d ₁ d ₂

6. Квадрат

S = a² S = 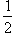d ²