МИНИСТЕРСТВО ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЕЖИ РЕСПУБЛИКИ КРЫМ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ РЕСПУБЛИКИ КРЫМ «СИМФЕРОПОЛЬСКИЙ ТЕХНИКУМ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА И ПРОМЫШЛЕННОСТИ»
РЕФЕРАТ
по дисциплине: «Математике»
на тему: Непрерывные дроби
ВЫПОЛНИЛ:
студент группы (1М-35)
Будко Никита
ПРЕПОДАВАТЕЛЬ:
преподаватель Казакова О.В.
г. Симферополь
2017 г.
Содержание
НЕПРЕРЫВНЫЕ ДРОБИ
НЕПРЕРЫВНЫЕ ДРОБИ. Последовательность, каждый член которой является обычной дробью, порождает непрерывную (или цепную) дробь, если ее второй член прибавить к первому, а каждую дробь, начиная с третьей, прибавить к знаменателю предыдущей дроби.
Например, последовательность 1, 1/2, 2/3, 3/4,..., n /(n + 1),... порождает непрерывную дробь
Где многоточие в конце указывает на то, что процесс продолжается бесконечно. В свою очередь непрерывная дробь порождает другую последовательность дробей, называемых подходящими. В нашем примере первая, вторая, третья и четвертая подходящие дроби равны
и
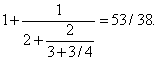
Их можно построить по простому правилу из последовательности неполных частных 1, 1/2, 2/3, 3/4,.... Прежде всего выпишем первую и вторую подходящие дроби 1/1 и 3/2. Третья подходящая дробь равна (2Ч1 + 3Ч3)/(2Ч1 + 3Ч2) или 11/8, ее числитель равен сумме произведений числителей первой и второй подходящих дробей, умноженных соответственно на числитель и знаменатель третьего неполного частного, а знаменатель равен сумме произведений знаменателей первого и второго неполных частных, умноженных соответственно на числитель и знаменатель третьего неполного частного. Четвертая подходящая дробь получается аналогично из четвертого неполного частного 3/4 и второй и третьей подходящих дробей: (3Ч3 + 4Ч11)/(3Ч2 + 4Ч8) или 53/38. Следуя этому правилу, находим первые семь подходящих дробей: 1/1, 3/2, 11/8, 53/38, 309/222, 2119/1522 и 16687/11986. Запишем их в виде десятичных дробей (с шестью знаками после запятой): 1,000000; 1,500000; 1,375000; 1,397368; 1,391892; 1,392247 и 1,392208. Значением нашей непрерывной дроби будет число x, первые цифры которого 1,3922. Подходящие дроби являются лучшим приближением числа x. Причем они поочередно оказываются то меньше, то больше числа x (нечетные – больше x, а четные – меньше).
Чтобы представить отношение двух положительных целых чисел в виде конечной непрерывной дроби, нужно воспользоваться методом нахождения наибольшего общего делителя. Например, возьмем отношение 50/11. Так как 50 = 4Ч11 + 6 или 11/50 = 1/(4 + 6/11), и, аналогично, 6/11 = 1/(1 + 5/6) или 5/6 = 1/(1 + 1/5), получаем:
Непрерывные дроби используются для приближения иррациональных чисел рациональными. Предположим, что x – иррациональное число (т.е. непредставимо в виде отношения двух целых чисел). Тогда, если n 0 – наибольшее целое число, которое меньше x, то x = n 0 + (x – n 0), где x – n 0 – положительное число меньше 1, поэтому обратное ему число x 1 больше 1 и x = n 0+ 1/ x 1. Если n 1 – наибольшее целое число, которое меньше x 1, то x 1 = n 1 + (x 1 – n 1), где x 1 – n 1 – положительное число, которое меньше 1, поэтому обратное ему число x 2 больше 1, и x 1 = n 1 + 1/ x 2. Если n 2 – наибольшее целое число, которое меньше x 2, то x 2 = n 2 + 1/ x 3, где x 3 больше 1, и т.д. В результате мы шаг за шагом находим последовательность неполных частных n 0, 1/ n 1, 1/ n 2,... непрерывной дроби, являющихся приближениями x.
Поясним сказанное на примере. Предположим, что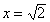 
, тогда
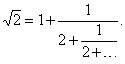
Первые 6 подходящих дробей равны 1/1, 3/2, 7/5, 17/12, 41/29, 99/70. Записанные в виде десятичных дробей они дают следующие приближенные значения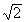 
: 1,000; 1,500; 1,400; 1,417; 1,4137; 1,41428. Непрерывная дробь для 
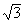имеет неполные частные 1, 1/1, 1/2, 1/1, 1/2, 1/1,.... Иррациональное число является корнем квадратного уравнения с целочисленными коэффициентами в том и только в том случае, если неполные частные его разложения в непрерывную дробь периодичны.
Непрерывные дроби тесно связны со многими разделами математики, например с теорией функций, расходящимися рядами, проблемой моментов, дифференциальными уравнениями и бесконечными матрицами. Если x – радианная мера острого угла, то тангенс угла x равен значению непрерывной дроби с неполными частными 0, x /1, - x 2/3, - x 2/7, - x 2/9,..., а если x – положительное число, то натуральный логарифм от 1 + x равен значению непрерывной дроби с неполными частными 0, x /1, 12 x /2, 12 x /3, 22 x /4, 22 x /5, 32 x /6,.... Формальным решением дифференциального уравнения x 2 dy / dx + y = 1 + x в виде степенного ряда является расходящийся степенной ряд 1 + x – 1! x 2 + 2! x 3 – 3! x 4 +.... Этот степенной ряд можно преобразовать в непрерывную дробь с неполными частными 1, x /1, x /1, 2 x /1, 2 x /1, 3 x /1, 3 x /1,..., а ее в свою очередь использовать для получения решения дифференциального уравнения x 2 dy / dx + y = 1 + x.
Список используемой литературы
https://hijos.ru/2011/06/22/nepreryvnye-drobi/
https://www.erudition.ru/ref/id.35904_1.html
https://ru.wikipedia.org/wiki