ЭКОНОМЕТРИКА
Учебно-методическое пособие
Киров
УДК 519.2(075.8)
Л 841
Допущено к изданию методическим советом факультета
экономики и менеджмента ФГБОУ ВПО «ВятГУ»
в качестве учебного пособия для студентов направлений
080100 «Экономика», 100700 «Торговое дело»
всех профилей подготовки очной формы обучения
Рецензенты:
кандидат физико-математических наук, доцент кафедры бизнес - информатики ФГБОУ ВПО «ВятГУ» Г.В.Бунькова
кандидат физико-математических наук, доцент кафедры математики ФГБОУ ВПО «Вятская ГСХА» А.В.Ряттель
К? Кошкин, Ю.Л.
Эконометрика. Учебно-методическое пособие: задания и методические указания к выполнению практических и лабораторных работ для студентов направлений 080500.62 «», 230700.62 «» очной формы обучения/ Ю.Л.Кошкин. – Киров: ПРИП ФГБОУ ВПО «ВятГУ», 2012. – 24 с.
УДК 519.2(075.8)
Учебное пособие содержит задания и указания по их выполнению в рамках самостоятельной работы студентов по дисциплине «Эконометрика», в нем представлены основные эконометрические модели, методика разыгрывания соответствующих исходных данных, методы идентификации.
Редактор Е.В.Кайгородцева
© Кошкин Ю.Л., 2012
© ФГБОУ ВПО «ВятГУ», 2012
Введение
Дисциплина «Эконометрика» изучается студентами – бакалаврами экономических направлений подготовки после изучения курса математической статистики и включает темы, которые традиционно вошли в состав предмета. В данном учебном пособии рассматриваются классические Эконометрические модели на основе использования современных методов и средств вычислительной техники.
Тема 1. Парная регрессия.
В работе по этой теме нужно сначала разыграть несколько вариантов регрессии вида
где f(x) – заданная неслучайная функция, параметры которой можно назначить самостоятельно;
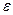- остатки, распределённые нормально с нулевым математическим ожиданием и подлежащим расчёту средним квадратическим отклонением.
Варианты в процессе разыгрывания будут отличаться значением индекса детерминации 
в пределах от 0,05 до 0,95 с шагом 0,1.
Задание 1. Разыграть 
значений фактора x по заданной зависимости
где 
- номер разыгрываемого наблюдения (строки табл.);
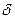- случайная величина (СВ), распределённая равномерно.
Для разыгрывания равномерно распределённой СВ на отрезке [0; 1] в SVB используется функция RND(1). Если интервал нужно изменить и сместить, то это нужно предусмотреть специально. Например, нужно распределение в интервале от -2 до +2. В этом случае 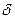=4*(RND(1)-0.5). Аргумент функции на её значение не влияет.
Пусть теперь требуется разыграть 
.
Размах 
при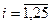 
составит 20 единиц. Множитель при RND нужно выбрать так, чтобы размах СВ 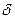составил бы 15-30% от размаха . Выберем его равным 4, тогда
при 
получим конкретную реализацию формулы (2): 
.
перед набором кодов загрузим систему Statistica, уберём «Приглашение» 
(х) и DataMiner (х). Далее следуем по меню: Файл -> создать -> Макрос(SVB). Придумываем имя (например, Yuri1) и ОК.
Коды для нашего примера могут быть такими
Option Base 1
Sub Main
n=25
kv=10
Dim s As New Spreadsheet
s.SetSize(n,kv+1)
s.VariableName(1)="x"
For v=1 To kv
s.VariableName(v+1)="y"&v
Next
х1=2 'лучше бы 5
For i=1 To n
s.Value(i,1)=x1+i-Sqr(i)+4*(Rnd(1)-0.5)
Next
s.Visible=True
End Sub
Для проверки х (первого столбца таблицы) «запускаем» коды (“Play”), редактируем (редко не бывает ошибок) и получаем таблицу:
| x | |
| 0,559664919 | |
| 1,84097006 | |
| -0,207661647 | |
| 0,281465255 | |
| 3,47833789 | |
| 3,12509069 | |
| 2,52161793 | |
| 6,93971415 | |
| 5,30567128 | |
| 4,95497769 | |
| 6,23343516 | |
| 7,57368489 | |
| 10,2352591 | |
| 11,7876995 | |
| 11,7463099 | |
| 12,2679425 | |
| 12,9424285 | |
| 13,4140473 | |
| 16,5183113 | |
| 17,4355605 | |
| 14,6110721 | |
| 15,478982 | |
| 18,2394 | |
| 18,4550199 | |
| 19,0994641 |
Чтобы посмотреть график можно выбрать такую последовательность в меню: Графика - > графики блоковых данных -> Линейный график: по столбцам. На графике должны быть видны и закономерность (f(i) и случайность (rnd). Случайность выглядит как некая «мохнатость» графика зависимости x от i – номера наблюдения, но если её не заметно, то надо увеличить коэффициент при RND. Если не видно закономерности, то либо велико 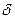(одна случайность), либо параметры f(i) подобраны неверно (функцию не видно).
В нашем случае степень случайности мы рассчитали предварительно. Однако, можно заметить, что х может принимать отрицательные значения. Конечно, во многих задачах это возможно, но при дальнейшей работе с разыгранными данными может потребоваться их логарифмирование. Поэтому лучше подобрать функции так, чтобы все результаты были строго положительны.
Задание 2. Разыграть kv=10 вариантов регрессии вида (1), отличающиеся значениями .
Пусть в нашем случае задана линейная регрессия: 
(зависимость определяется вариантом задания).
Для разыгрывания 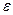в SVB служит функция RndNormal(se), аргументом служит значение среднеквадратичного отклонения 
, а математическое ожидание равно нулю.
Значение неизвестно, но его можно вычислить по известному (заданному в наборе) значению , пользуясь выражением:
откуда 
, где
и 
- остаточная и полная суммы квадратов отклонений соответственно.
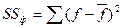- факторная сумма квадратов отклонений;
из (1); 
- среднее значение для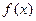 
.
Тогда 
,
где 
- факторная дисперсия. Окончательно 
.
С учётом изложенного, после последнего next вставляем коды:
a=5 'лучше бы 150
b=2
sf=0
sf2=0
For i=1 To n
x=s.Value(i,1)
f=a+b*x
sf=sf+f
sf2=sf2+f*f
Next
df=sf2/n-sf*sf/n/n 'факторная дисперсия
For v=1 To kv
r2=0.1*v-0.05
se=Sqr(df*(1-r2)/r2)
For i=1 To n
e=RndNormal(se)
x=s.Value (i,1)
y=a+b*x+e
s.Value (i,v+1)=Format(y,"0.000")
Next
Next
Получаем таблицу:
| x | y1 | y2 | y3 | y4 | y5 | y6 | y7 | y8 | y9 | y10 | |
| 0,559664919 | 106,647 | 31,513 | 13,275 | 18,98 | -26,861 | 5,997 | 15,647 | 6,429 | 12,968 | 6,975 | |
| 1,84097006 | -44,396 | 13,481 | -11,703 | -0,765 | 34,162 | 6,189 | 0,668 | 12,371 | 16,65 | 9,25 | |
| -0,207661647 | -56,189 | 16,546 | 18,529 | 5,104 | 31,553 | -0,879 | 3,76 | 1,99 | 6,345 | 2,436 | |
| 0,281465255 | -6,619 | -28,061 | -34,435 | 11,776 | -3,897 | -10,797 | 5,423 | -0,775 | 1,288 | 7,981 | |
| 3,47833789 | -34,617 | 14,305 | 12,168 | 35,621 | 31,053 | 23,153 | 1,788 | 14,703 | 14,169 | 15,855 | |
| 3,12509069 | 14,756 | 18,914 | 5,024 | 22,408 | -6,482 | 1,404 | 17,217 | 8,923 | 14,124 | 10,994 | |
| 2,52161793 | 64,481 | 23,88 | -3,299 | -6,218 | 6,359 | 9,18 | 10,813 | 8,422 | 8,479 | 9,572 | |
| 6,93971415 | -51,321 | 53,154 | 14,609 | 17,358 | 31,906 | 14,218 | 23,462 | 25,91 | 11,912 | 14,547 | |
| 5,30567128 | -9,873 | 3,9 | 6,215 | 22,855 | 12,253 | 24,755 | 4,932 | 12,721 | 10,546 | 20,071 | |
| 4,95497769 | -36,448 | 12,541 | 28,381 | 38,132 | -0,005 | 7,856 | 25,476 | 29,649 | 24,625 | 17,107 | |
| 6,23343516 | -13,525 | -13,898 | 32,424 | 18,713 | 4,7 | 16,318 | 17,133 | 27,622 | 30,41 | 12,902 | |
| 7,57368489 | 20,398 | -39,242 | 32,557 | 19,309 | 41,2 | 4,502 | 28,476 | 22,62 | 21,648 | 17,183 | |
| 10,2352591 | -20,576 | -53,627 | 6,634 | 17,356 | 34,483 | 17,576 | 8,285 | 18,213 | 24,677 | 26,976 | |
| 11,7876995 | 12,417 | 27,2 | 47,665 | 10,083 | 15,473 | 36,415 | 39,913 | 35,826 | 31,03 | 29,757 | |
| 11,7463099 | 102,583 | 55,346 | 12,908 | 26,396 | 21,894 | 38,643 | 14,94 | 32,399 | 36,003 | 26,049 | |
| 12,2679425 | 46,794 | 47,129 | 12,561 | 26,775 | 40,462 | 32,54 | 13,766 | 25,007 | 25,396 | 22,284 | |
| 12,9424285 | 127,217 | 29,307 | 28,083 | 63,854 | 43,016 | 29,636 | 35,055 | 38,61 | 32,199 | 27,831 | |
| 13,4140473 | 13,736 | 32,261 | 62,745 | 23,738 | 11,622 | 4,962 | 21,126 | 31,919 | 24,813 | 27,494 | |
| 16,5183113 | 39,743 | -27,343 | 33,878 | 62,5 | 27,807 | 26,426 | 30,368 | 38,535 | 46,932 | 39,559 | |
| 17,4355605 | 105,767 | 17,962 | 17,549 | 45,717 | 38,026 | 24,816 | 50,308 | 52,668 | 44,681 | 41,343 | |
| 14,6110721 | 27,207 | 27,175 | 39,743 | 48,414 | 18,827 | 21,085 | 45,886 | 22,674 | 25,255 | 30,179 | |
| 15,478982 | 41,914 | 45,145 | 24,209 | 43,438 | 10,253 | 45,718 | 29,949 | 40,296 | 43,132 | 37,301 | |
| 18,2394 | -26,429 | 31,31 | 49,727 | 67,391 | 72,203 | 50,331 | 31,061 | 47,324 | 38,914 | 43,71 | |
| 18,4550199 | 45,556 | 8,802 | 33,569 | 38,132 | 62,931 | 51,929 | 34,089 | 42,458 | 45,753 | 41,678 | |
| 19,0994641 | 73,033 | 72,711 | 24,362 | 68,717 | 43,596 | 44,559 | 53,126 | 38,413 | 45,48 | 45,574 |
Далее для любого из разыгранных вариантов можно увидеть график регрессии (1). Например, выбираем последовательность: Графика -> 2М – графики -> Диаграммы рассеяния. Далее нужно задать в качестве аргумент Х переменную х, а в качестве функции одну или несколько (хоть все) разыгранные у.
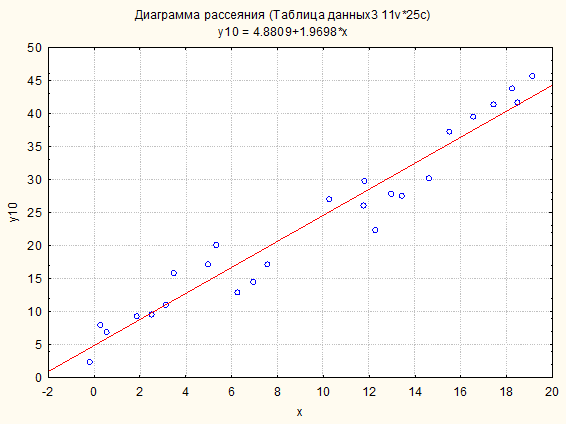
По виду разыгранных функций, возможность логарифмирования не просматривается. Проще всего обеспечить положительность всех значений можно за счёт увеличения параметра а до, скажем, 150.
В отчёте привести:
1) постановку задачи, включая заданные функции и выбранные значения параметров.
2) порядок разыгрывания коды SVB.
3) графики для x(i) и y1(x) и некоторых других по выбору, графики всех y(x).
4) таблицу для всех разыгранных вариантов и выводы о разбросе у в зависимости от .
Варианты заданий
| f(x) | f(i) | ||||
| 
| 
| 
| 
| |
| 1 (0,15) | 2 (0,25) | 3 (0,35) | ||
| 4 (0,45) | 5 (0,55) | |||
| 6 (0,65) | 7 (0,75) | 8 (0,85) | ||
| 9 (0,95) | 10 (0,85) | 11 (0,75) | 12 (0,65) | |
| 13 (0,55) | 14 (0,45) | 15 (0,35) | 16 (0,25) | |
| 17 (0,35) | 18 (0,45) | 19 (0,55) | 20 (0,65) | |
| 21 (0,75) | 22 (0,85) | 23 (0,55) |
В скобках указано для использования конкретного варианта в следующей работе.
Задание 3. Рассчитать параметры и основные характеристики регрессии в среде Excel без использования специальных функций. В качестве регрессионных зависимостей выбрать линейную и какую-либо из нелинейных (лучше разыгрываемую, но не обязательно). Не забыть рассчитать величины r, Vx и Vy.
Задание 4. Реализовать расчёты с помощью статистических функций ЛИНЕЙН и ЛГРФПРИБЛ. Методику реализации см. в [1], с.29-31.
Задание 5. Реализовать расчёты в ПАКЕТЕ АНАЛИЗА. См. [1], с.31-35.
В отчёте по заданию 1 привести сначала постановку задачи, включая конкретные (выбранные в виде чисел) исходные данные и процесс реализации решения как до кодов, так и далее – программные коды. После этого привести необходимые графики и результаты (функции и численные).
По каждому заданию из 2-4 привести постановки задач и результаты.
В выводах по лабораторной работе №1 сравнить общие результаты разных способов решения (хотя бы для линейной зависимости) и сравнить эти способы с точки зрения пользователя.
Тема 2. Множественная регрессия.
Задание 1. Разыграть данные для уравнения регрессии:
где 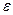- нормально распределённая случайная величина (СВ)
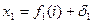
- номер разыгрываемого «наблюдения», ;
- объём разыгрываемой совокупности;
- нормально распределённые СВ;
- заданные (вариантом) неслучайные функции.
Для каждой из СВ необходимо задать среднее квадратичное отклонение.
Задание 2. Рассчитать параметры уравнения регрессии в среде Excel и Statistica.
В отчёте привести:
- формулировки заданий со всеми исходными данными
- коды для разыгрывания и таблицу результатов
- двумерные графики 
и 
- трёхмерный график 
, аппроксимированный сплайном
- распечатки Excel и Statistica
- запись уравнения регрессии в обычном и стандартизированном масштабах.
Процесс подгонки параметров при разыгрывании (см. ниже) можно не показывать, только окончательные результаты подгонки.
Варианты
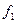
- 1 2 3 20
4 5 - 6 7
8 - 9 10 11
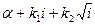12 13 14 15 -
16 17 18 - 19
Коды для разыгрывания 16-го варианта
Option Base 1
Sub Main
n=25'объём выборки
Rem параметры для f1
k=60
alfa=-3
Rem параметры для f2
Bet=3
k1=20
k2=-1
se1=2'среднее квадратичное для f1
se2=20
Rem параметры для у, исходно взяли наугад, для них будет нужна подгонка
a=15
b1=0.5
b2=0.3
sey=1500
Dim s As New Spreadsheet
s.SetSize (n,3)
s.VariableName (1)="x1"
s.VariableName (2)="x2"
s.VariableName (3)="y"
For i=1 To n
f1=alfa+k*Exp(-i)
x1=f1+RndNormal(se1)
s.Value (i,1)=x1
f2=Bet+k1*i+k2*i*i
x2=f2+RndNormal(se2)
s.Value (i,2)=x2
y=a+b1*x1+b2*x2
s.Value (i,3)=y+RndNormal(sey)
Next
s.Visible =True
End Sub
В результате получим таблицу
| x1 | x2 | y | |
| 20.5172242 | 43.2754837 | -477.326543 | |
| 5.76236496 | 72.9517458 | 820.479524 | |
| 0.477847564 | 87.4345831 | 675.663551 | |
| -4.56831706 | 37.1698256 | -4388.30124 | |
| -0.564231311 | 57.3499941 | 1394.23953 | |
| -0.53526118 | 87.5713173 | 731.424427 | |
| -2.17549397 | 85.038874 | -807.813644 | |
| -1.07859746 | 68.2482081 | -194.710409 | |
| -0.900943718 | 122.515665 | -2284.47813 | |
| -3.2872035 | 112.789426 | 212.499083 | |
| -3.83293012 | 101.142029 | -1151.44435 | |
| -5.69282156 | 97.1148723 | -2584.6406 | |
| -2.33856604 | 104.30968 | 468.243854 | |
| -4.12731518 | 65.3799323 | -780.169163 | |
| 0.509496262 | 116.712559 | 704.805453 | |
| -2.51921225 | 53.4085225 | -1285.17552 | |
| -1.39475605 | 73.3897643 | 1582.51138 | |
| -6.72855501 | 13.3411308 | -1700.94679 | |
| -0.238082788 | 99.2292673 | 2648.40227 | |
| -2.26487806 | 46.9624241 | -1789.81258 | |
| -4.36091125 | 22.2977823 | -746.691119 | |
| -3.52143103 | -46.1529273 | -971.597643 | |
| -1.34508357 | -91.6195514 | 3070.8122 | |
| -0.837803271 | -109.054958 | 1849.27652 | |
| -4.38528994 | -150.179369 | -1939.87569 |
Графики для независимых переменных (процесс построения см. в теме 1)
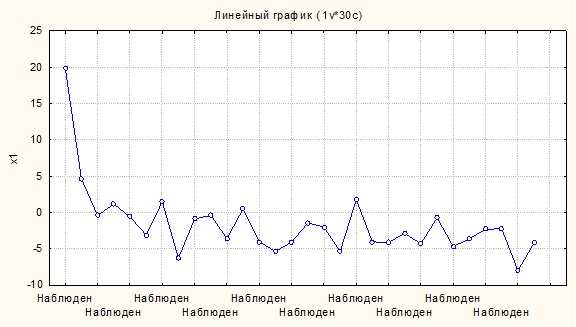
Если используем параболу, нужно так подобрать параметры к1 и к2, чтобы на графике был заметен экстремум (ну а знаки этих коэффициентов должны быть разными).
График поверхности для зависимой переменной
Для построения нужно выбрать: Графика -> 3M XYZ графики -> графики поверхностей, далее выбрать оси, выделить галочкой необходимость показа исходных данных на поверхности и подгонку точек поверхности сплайнами (можно и другим способом).
По виду графика можно предположить, что получили что-то не очень похожее на линейную зависимость (плоскость). Возможно, параметры для разыгрывания у придётся подгонять. Но в любом случае предварительно надо провести анализ полученной зависимости для разыгранных данных. (Выбираем: Анализ –> множественная регрессия, задаём зависимой переменной у, независимыми х1 и х2, ОК). Для просмотра итоговых результатов регрессии получим таблицу:
| Итоги регрессии для зависимой переменной: y (Таблица данных6) R=.27570898 R2=.07601544 Скорректир. R2= ----- F(2,22)=.90496 p | ||||||
| БЕТА | Стд.Ош. | B | Стд.Ош. | t(22) | p-уров. | |
| Св.член | -76.5160 | 428.3401 | -0.178634 | 0.859860 | ||
| x1 | 0.270236 | 0.205807 | 90.4978 | 68.9216 | 1.313055 | 0.202696 |
| x2 | -0.084853 | 0.205807 | -2.0231 | 4.9070 | -0.412295 | 0.684113 |
Столбец «В» позволяет записать уравнение регрессии, т.к. содержит найденные (рассчитанные) значения его параметров:
Здесь под значениями соответствующих параметров (снизу) записаны их стандартные ошибки из столбца «Стд.ош». Значимость каждого из параметров определяется значением t-критерия (предпоследний столбец) и уровнем значимости (последний). В столбце БЕТА приведены значения стандартизированных коэффициентов регрессии (позволяющие ранжировать факторы по их влиянию на результат: чем больше по модулю коэффициент, тем сильнее влияет соответствующий фактор). Стандартизированное уравнение в нашем случае получилось таким:
,
то есть для полученной модели х1 сильнее влияет на результат.
По данным таблицы можно утверждать, что мы разыграли данные, которые вряд ли могут заинтересовать эконометриста, то есть позволят ему построить модель, пригодную для осуществления основных целей эконометрического моделирования, в частности, для прогнозирования. Уровень значимости для свободного члена составляет 0,860, таким образом вероятность того, что он незначим р=0,86=86%! Слишком велики значения уровней значимости и для коэффициентов регрессии (обычно для хороших моделей они не превышают 10%). Кроме того мы видим, что стандартные ошибки параметров превышают по модулю сами значения. Можно заметить, что основные характеристики надёжности уравнения в целом (в «шапке» таблицы) также далеки от «идеальных».
Так как на данном этапе нашей целью является разыгрывание (генезис) таких данных, которые должны быть интересными для практики, попытаемся подогнать параметры разыгрываемой функции: a, b1, b2 и 
(среднее квадратичное отклонение 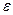, обозначенное в кодах переменной sey).
Подгонка параметров разыгрываемого уравнения
Угадать случайно нужные значения вряд ли удастся (уже не удалось), поэтому попробуем предложить некоторую последовательность шагов. (В некотором смысле алгоритм, хотя и не формализованный). Нумерация шагов условна и их порядок в процессе подгонки может оказаться другим.
1. Предположим сначала, что всё идеально: исключим (пока)
случайность 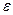, то есть примем =0 (в кодах sey=0). Другие параметры пока не «трогаем», иначе не поймём, что от чего изменилось. В результате получим идеальную линейную зависимость(плоскость):
и таблицу
| Итоги регрессии для зависимой переменной: y (Таблица данных9) R=1.00000000 R2=1.00000000 Скорректир. R2=1.00000000 F(2,22)=495E14 p | |||||||||||||
| БЕТА | Стд.Ош. | B | Стд.Ош. | t(22) | p-уров. | ||||||||
| Св.член | 15.00000 | 0.000000 | 0.00 | ||||||||||
| x1 | 0.135762 | 0.000000 | 0.50000 | 0.000000 | 0.00 | ||||||||
| x2 | 0.993062 | 0.000000 | 0.30000 | 0.000000 | 0.00 | ||||||||
Очевидно, что получили то, что и разыгрывали: a=15; b1=0,05; b2=0,03. Значимость тоже идеальна (все вероятности незначимости равны нулю), стандартные ошибки тоже нулевые. То есть разыгранные данные (таблицу мы не привели) тоже не интересны: в реальных данных всегда есть неидеальности в виде ошибок, ненулевых уровней значимости, а коэффициент детерминации (R) и его квадрат не равны 1 (см. «шапку»).
2. Ухудшим идеальность. Примем sey=5 (уменьшили, но наудачу). Получим:
| Итоги регрессии для зависимой переменной: y (Таблица данных12) R=.98009139 R2=.96057913 Скорректир. R2=.95699541 F(2,22)=268.04 p | ||||||
| БЕТА | Стд.Ош. | B | Стд.Ош. | t(22) | p-уров. | |
| Св.член | 14.33433 | 1.141029 | 12.56264 | 0.000000 | ||
| x1 | 0.084811 | 0.042428 | 0.33419 | 0.167184 | 1.99893 | 0.058119 |
| x2 | 0.970677 | 0.042428 | 0.31108 | 0.013597 | 22.87815 | 0.000000 |
Видим, что плоскость не такая уж и идеальная, но параметры a и b2 надо бы «ухудшить» (приблизить к реальным). Сразу оба не будем (запутаемся), примем b2=0,1. Здесь следует отметить, что чем больше значение параметра, тем он значимее (весомее), если р-уров. очень велик, то параметр незначим (его в первом приближении можно обнулить, а тогда для самого первого случая, до подгонки, когда все параметры незначимы, мы по сути получили «уравнение регрессии» у=0). Далее не будем показывать подгоночные (отладочные) поверхности, только таблицы. При b2=0,1 получим
| Итоги регрессии для зависимой переменной: y (Таблица данных15) R=.77310753 R2=.59769525 Скорректир. R2=.56112210 F(2,22)=16.342 p | ||||||
| БЕТА | Стд.Ош. | B | Стд.Ош. | t(22) | p-уров. | |
| Св.член | 13.78887 | 1.286728 | 10.71622 | 0.000000 | ||
| x1 | 0.189226 | 0.136011 | 0.28367 | 0.203893 | 1.39126 | 0.178058 |
| x2 | 0.770142 | 0.136011 | 0.08578 | 0.015150 | 5.66235 | 0.000011 |
Для a и b2 почти ничего не изменилось, а значимость b2 ухудшилась. Нельзя однозначно предложить что лучше: ухудшать a или b2 или же улучшать b1. Но коли уж взялись за ухудшение значимости b2, то продолжим: пусть b2=0,01 (остальные параметры «не трогаем»). Получим
| Итоги регрессии для зависимой переменной: y (Таблица данных18) R=.61705335 R2=.38075483 Скорректир. R2=.32445982 F(2,22)=6.7636 p | ||||||
| БЕТА | Стд.Ош. | B | Стд.Ош. | t(22) | p-уров. | |
| Св.член | 17.20434 | 0.868802 | 19.80238 | 0.000000 | ||
| x1 | 0.574551 | 0.167791 | 0.50410 | 0.147216 | 3.42421 | 0.002427 |
| x2 | -0.233748 | 0.167791 | -0.01509 | 0.010835 | -1.39309 | 0.177509 |
b2 сильно «поплохел», примем b2=0,04 и получим
| Итоги регрессии для зависимой переменной: y (Таблица данных21) R=.58067467 R2=.33718307 Скорректир. R2=.27692699 F(2,22)=5.5958 p | ||||||
| БЕТА | Стд.Ош. | B | Стд.Ош. | t(22) | p-уров. | |
| Св.член | 13.37021 | 1.191173 | 11.22441 | 0.000000 | ||
| x1 | 0.256785 | 0.173694 | 0.31450 | 0.212731 | 1.47837 | 0.153483 |
| x2 | 0.530440 | 0.173694 | 0.04222 | 0.013824 | 3.05387 | 0.005819 |
Хотя b1 не очень значим, самым нереалистичным (суперзначимым) сейчас стал а, уменьшим его до а=5.
| Итоги регрессии для зависимой переменной: y (Таблица данных24) R=.57494292 R2=.33055937 Скорректир. R2=.26970113 F(2,22)=5.4316 p | ||||||
| БЕТА | Стд.Ош. | B | Стд.Ош. | t(22) | p-уров. | |
| Св.член | 3.467756 | 1.303647 | 2.660042 | 0.014302 | ||
| x1 | 0.503343 | 0.176224 | 0.665548 | 0.233013 | 2.856270 | 0.009180 |
| x2 | 0.358344 | 0.176224 | 0.032626 | 0.016045 | 2.033459 | 0.054243 |
В принципе процесс подгонки можно закончить и принять окончательно
Здесь одной звёздочкой обозначены значения параметров, обеспеченных уровнем значимости от 5 до 10%, двумя – от 1 до 5%, тремя – менее 1%. Иногда, при уровне значимости менее 0,1%, применяют 4 звёздочки.
Тема 3. Имитация и анализ аддитивной модели временного ряда (ВР).
Задание 1. Разыграть (или использовать реальные исходные данные) аддитивную модель ВР:
Y=T+S+E
с числом случаев n>=48,
с заданным видом тренда Т и количеством случаев k на период циклической компоненты S:
S=Am*sin(2*Pi*t/k-Phi), 0<=Phi<=2*Pi,
где случайная величина Е распределена нормально (подобрать параметры распределения), As – амплитуда колебаний,
Phi – фазовый сдвиг.
Задание 2. Провести анализ полученного ряда (выделить Т, S и Е) и сделать прогноз на 6 дискретов времени.
Варианты:
Т a+b*t a+b*sqr(t) a+b*ln(t) a+b*sin(2*pi*t/(3*n))
k
5 1 2 3 4
7 5 6 7 8
9 9 10 11 12
11 13 14 15 16
13 17 18 19 20
15 21 22 23 24
В отчёте привести:
1) формулировку задания с конкретными значениями числовых параметров,
2) коды SVB,
3) результаты рaзыгрывания в виде таблицы и траектории ВР,
4) процесс расчётов (с пояснениями),
5) полученную модель и прогноз,
6) возможные выводы (например, о совпадении тренда, хотя в расчётах при выделении Т разрешается выбрать его форму не ту, что разыгрывали).
При использовании реальных данных вместо первых трёх пунктов привести таблицу и траекторию реального ВР.
Тема 4. Модели с распределённым лагом.
Предполагается, что ряд-результат 
зависит от значений ряда-фактора 
в этот и предшествующие периоды времени:
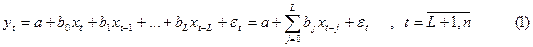
где 
- максимальная длина лага.
При 
нужно оговорить начальные условия:
Если коэффициенты ряда (1) имеют геометрическую структуру, то получаем модель Л.М.Койка, в которой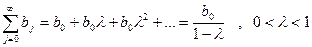 
Если лаг представлен полиномиальной структурой 
,
то получим модель Ш.Алмон, где 
- порядок полинома.
Задание 1. Разыграть модель (2), (1) с полиномиальным лагом заданной длины L. Коэффициенты 
подобрать исходя из заданной структуры.
Пусть, например, задано L=5, а структура предполагает 2 экстремума, первый из которых - минимум. Представим эту структуру в произвольном масштабе (Рис.1) и выберем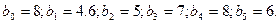 
(Округлять можно грубо).
Рис.1.
В качестве ряда-фактора в этой работе предлагается взять ряд из лабораторной работы № 3. Пусть он был таким: 
Пусть Т=0, 
, Е – центрированная нормальная случайная величина со средним квадратическим отклонением sx. Для величины 
в формулах (1) и (2) выберем такое же распределение с отклонением sy.
Коды для разыгрывания могут быть такими.
Sub Main
Dim b()
n=100
Dim s As New Spreadsheet
s.SetSize (n,2)
s.VariableName (1)="x"
s.VariableName (2)="y"
l=5
a=0
sy=0.5'sigma y
ReDim b(l)
b(0)=8:b(1)=5:b(2)=5:b(3)=7:b(4)=8:b(5)=6
am=2
k=11
phi=PI/8
sx=2
For t=1 To l
s.Value (t,1)=am*Sin(2*PI*t/k+phi)+RndNormal(sx)
s.Value (t,2)=a+RndNormal(sy)
For j=0 To t-1
s.Value (t,2)=s.Value (t,2)+b(j)*s.Value(t-j,1)
Next
Next
For t=l+1 To n
s.Value (t,1)=am*Sin(2*PI*t/k+phi)+RndNormal(sx)
s.Value (t,2)=a+RndNormal(sy)
For j=0 To l
s.Value (t,2)=s.Value (t,2)+b(j)*s.Value(t-j,1)
Next
Next
s.Visible =True
End Sub
После запуска получим таблицу
| X | y | |
| -1,9411385 | -16,7768368 | |
| 0,849624365 | -2,33967247 | |
| 0,118055052 | -3,55255317 | |
| -1,10288693 | -18,0450776 | |
| 2,41049858 | 4,72976147 | |
| -0,372484895 | -0,536349481 | |
| -3,5455313 | -19,3562274 | |
| -2,05780492 | -27,0894901 | |
| 0,719346674 | -11,3390325 | |
| -1,19467429 | -29,6994593 | |
| 3,60738447 | -18,5171309 | |
| 3,20137978 | 4,97429419 | |
| … | … | … |
| 2,32737119 | 77,8169354 | |
| 2,09379941 | 69,0489157 | |
| -3,63971492 | -6,53478214 | |
| -2,09356424 | -26,6057104 | |
| 0,327322693 | -12,6422892 | |
| -2,99574413 | -27,5188595 | |
| 3,30351166 | -18,3412585 | |
| 1,29631682 | -24,2078765 |
Посмотреть оба графика можно после таких выборов в меню: Графика à 2М Графики à Линейные графики (для переменных) à Дополнительно à С двойной осью Y à левая ось: 1-х, правая 2-у и ОК.
Задание 2. Провести анализ разыгранных данных в среде Statistica.
Выбираем: Анализ à Углубленные методы анализа à Временные ряды и прогнозирование à Анализ распределенных лагов à при выборе переменных: Выбрать все и ОК
На панели «Анализ распределенных лагов» выделяем цветом зависимую переменную Y, точкой выделяем Полиномиальные лаги Алмона (не надо бы склонять женскую иностранную фамилию), выбираем в качестве независимой переменную X.
Для каждого анализа нужно задать длину лага (вряд ли имеет смысл большее значение, чем разыгранное, но можно попробовать) и порядок полинома ord (в диалоге заполнить окно p<лаг). После всех выборов (лаг=5; р=4) нажимаем ОК (Начать анализ). Получим таблицу:
| Полиномиал. лаги Алмона; Коэффициенты регрессии (Таблица данных2) Незав: X Зав: Y Лаг: 5 Пор. полин.: 4 R=,4264 R-квадр.=,1818 N: 95 | ||||
| Регресс. | Станд. | t(89) | p | |
| 8,278801567454 | 4,337102361409 | 1,908832413345 | 0,059506232736 | |
| 5,157486434160 | 3,874236990848 | 1,331226366984 | 0,186514550370 | |
| 4,842374645857 | 2,929623755507 | 1,652899843113 | 0,101874796276 | |
| 6,203873500944 | 2,951951807511 | 2,101617473957 | 0,038412896684 | |
| 7,566196744460 | 3,874549758746 | 1,952793799429 | 0,053986279601 | |
| 6,707364568074 | 4,381748120309 | 1,530750829101 | 0,129377790046 |
Далее можно провести новый анализ, допустим: лаг=5, р=3 (как разыгрывали, так как два экстремума можно реализовать полиномом 3-го порядка):
| Полиномиал. лаги Алмона; Коэффициенты регрессии (Таблица данных2) Незав: X Зав: Y Лаг: 5 Пор. полин.: 3 R=,4264 R-квадр.=,1818 N: 95 | ||||
| Регресс. | Станд. | t(89) | p | |
| 8,336016596435 | 4,115300244627 | 2,025615654002 | 0,045799333350 | |
| 5,042239459162 | 2,841768307734 | 1,774331653091 | 0,079427975908 | |
| 4,914016886986 | 2,423344037655 | 2,027783430924 | 0,045572882695 | |
| 6,275554394738 | 2,449419648835 | 2,562057668527 | 0,012086854697 | |
| 7,451057497252 | 2,844414481934 | 2,619539994813 | 0,010350754671 | |
| 6,764731709362 | 4,160745510382 | 1,625846063520 | 0,107518352017 |
Судя по последнему столбцу уровни значимости всех коэффициентов улуч