Комплексные числа.
1. Понятие мнимой единицы.
Пусть существует такое число, квадрат которого равен (-1). Обозначим это число буквой i, тогда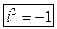 
. Число i будем называть мнимой единицей. Тогда 
.
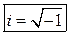Рассмотрим степени мнимой единицы:
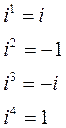
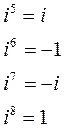
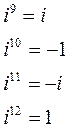
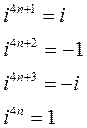
Таким образом, если показатель степени числа i:
- делится на 4, то значение степени равно1;
- если при делении показателя степени на 4 в остатке получается 1, то значение степени равно i;
- если при делении показателя на 4 получается остаток 2, то значение степени равно -1;
- если при делении на 4 остаток равен 3, то значение степени равно –i.
2. Определение комплексного числа
Числа вида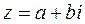 
, где 
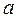и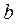 
- действительные числа; 
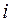- мнимая единица, называется комплексным числом.
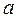- действительная часть числа, 
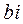- мнимая часть комплексного числа, 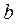- коэффициент при мнимой части.
Комплексные числа по виду делятся:
- если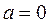 
, то комплексное число 
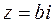- называется чисто мнимым.
- если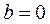 
, то комплексное число 
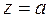- называется чисто действительным.
- есл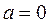и и 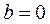, то комплексное число равно нулю.
- два комплексных числа называются равными тогда и только тогда, когда равны их действительные и мнимые части.
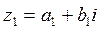и 
.
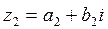
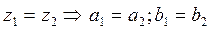- два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью.
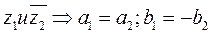
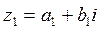и 
.
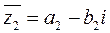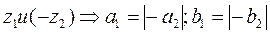
- два комплексных числа называются противоположными, если они отличаются друг от друга знаками перед действительной и мнимой частям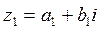и.
и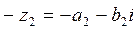 
.
3. Геометрическое изображение комплексного числа
Комплексное число 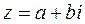можно изобразить точкой Z в координатной плоскости с координатами (a; b). Для этого выберем на плоскости декартову прямоугольную систему координат. Действительные числа изображаются точками оси абсцисс, которую называют действительной (вещественной) осью, чисто мнимые числа – точками оси ординат, которую называют мнимой осью.
Каждой точке плоскости с координатами (a; b) соответствует один и только один вектор с началом О (0;0) и концом Z(a; b). Поэтому комплексное число 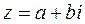можно изобразить в виде вектора 
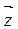с началом в точке О(0;0) и концом в точке Z(a; b).
Изобразим в координатной плоскости числа: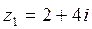 
; 
; 
;
; 
.
 |
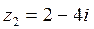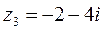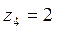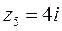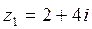- Комплексные числа и 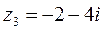- противоположные, векторы симметричны относительно начало координат.
- Комплексное число 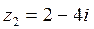является сопряженным числу 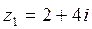и их вектора симметричны относительно оси абсцисс.
4. Модуль и аргумент комплексного числа.
Любое комплексное число имеет модель и аргумент.
Модулем комплексного числа 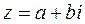называется длина вектора 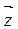, которую можно найти по формуле 
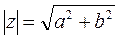. Обозначается модуль комплексного числа буквой r 
.
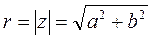Аргументом комплексного числа называется угол φ, который образует вектор 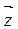с положительным направлением оси абсцисс. Величину угла φ можно найти: 
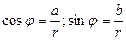. Эта система имеет бесчисленное множество решений вида 
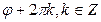. Таким образом, комплексное число имеет бесконечное множество аргументов, отличающихся друг от друга на число, кратное 
.
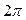5. Формы записи комплексного числа.
Существует три формы записи комплексного числа:
1. Алгебраическая форма: .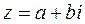
2. Тригонометрическая форма: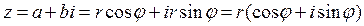 
.
3.показательная форма комплексного числа (формула Эйлера):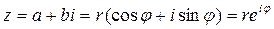 
.
Правило перехода от алгебраической формы комплексного числа к тригонометрической:
1. Находят модуль комплексного числа: .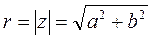
2. для нахождения аргумента сначала определяют геометрически, в какой четверти находится точка комплексного числа.
3. составляем уравнения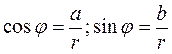 
и по решению одного из них определяем аргумент.
4. записываем комплексное число в тригонометрической форме.
Совместные действия над комплексными числами.
Пусть даны два комплексных числа, заданных в алгебраической, тригонометрической и показательной формах.
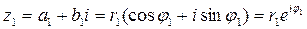
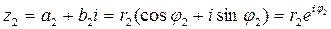
Тогда:
1. Сложение и вычитание выполняются над комплексными числами, заданных в алгебраической форме:
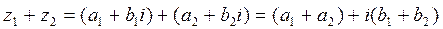
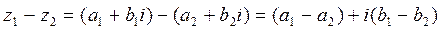
2. При умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
.
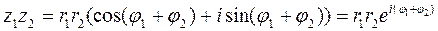3. При делении комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются:
.
4. При возведении в степень комплексного числа, заданного в тригонометрический форме, модуль числа нужно возвести в n -ю степень, а аргумент умножить на число n (формула Муавра):
.
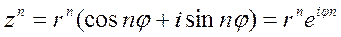5. Корень n-й степени из комплексного числа имеет ровно n значений, которые находятся по формуле: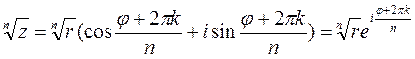 
.
Пример 1. Выполнить действия над комплексными числами, представив результат в алгебраической форме:
1) (2+3 i)(3− i). Решение:(2+3 i)(3− i)=6−2 i +9 i −3 i 2=6+7 i +3=9+7 i. Ответ: 9+7 i.
2) z 1 = 3 + i, z 2 = 2 i. Найти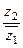 
Решение.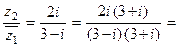 
.
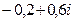3) z 1=1 + 2 i, z 2 = − 3 i. Найти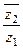 
. Решение.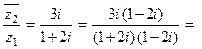 
.
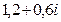4) (1+ i)(3+ i)3− i −(1− i)(3− i)3+ i.
Решение.
(1+ i)(3+ i)3− i −(1− i)(3− i)3+ i =(1+ i)(3+ i)(3+ i)(3− i)(3+ i)−
−(1− i)(3− i)(3− i)(3+ i)(3− i)=9+15 i +7 i 2+ i 39− i 2−9−15 i +7 i 2− i 39− i 2=
=9+15 i −7− i −9+15 i +7− i 10=2810 i =145 i.
Ответ: 145 i.
Пример 2. Найти действительные решения следующего уравнения:
(1+ i) x +(−2+5 i) y =−4+17 i.
Решение.
(1+ i) x +(−2+5 i) y =−4+17 i ⇒ x + xi −2 y +5 yi =−4+17 i ⇒(x −2 y)+(x +5 y) i =−4+17 i ⇒
{ x −2 y =−4 x +5 y =17⇒{ x =2 y −42 y −4+5 y =17⇒{ x =2 y =3.
Ответ: x =2; y =3.
Пример 3. Решить уравнение (2 + i) х 2 – (5 – i) х + (2 – 2 i) = 0.
Решение.По формуле корней квадратного уравнения имеем:
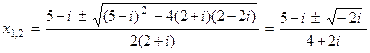
Извлекая корень квадратный из числа – 2i, получаем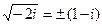 
.
Следовательно,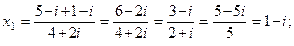 
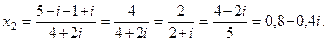
Ответ: 1 – i; 0,8 – 0,4 i.
Пример 4. Найти значение функции
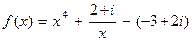при x = 1 − 2 i.
Решение.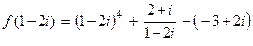 
.
Вычислим второе слагаемое: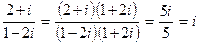 
.
Вычислим первое слагаемое: ((1 − 2i)2)2 = 1 − 8i − 24 + 32i + 16 = − 7 + 24i.
Таким образом, f (l − 2i) = (− 7 + 24i) + i − (− 3 + 2i) = − 4 + 23i.
Ответ: − 4 + 23 i.
Пример 5. Решить уравнение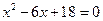 
.
Решение. Дискриминант данного уравнения: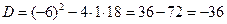 
меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
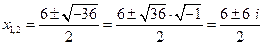, т.е. 
; 
.
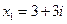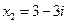Пример 6. Вычислить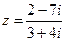 
и указать вещественную и мнимую части полученного комплексного числа.
Решение. Действуя в соответствии с правилами получаем:
;
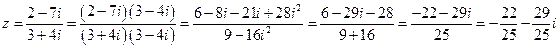поэтому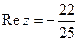 
, 
.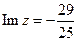