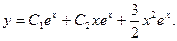Линейные дифференциальные уравнения высших порядков.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным дифференциальным уравнением n – го порядка называется любое уравнение первой степени относительно функции у и ее производных 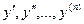 вида:
вида: 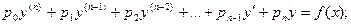
где p0, p1, …,pn – функции от х или постоянные величины, причем p0 ¹ 0.
Если f(x) = 0, то уравнение называется линейным однородным уравнением, если f(x) ¹ 0, то называется линейным неоднородным уравнением, если все коэффициенты p0, p1, p2, … pn – постоянные числа, то уравнение
Уравнение вида 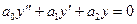 , где
, где  – постоянные называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами.короче.
– постоянные называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами.короче.
Теорема: если 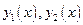 – частные решения уравнения
– частные решения уравнения 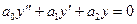 , причем
, причем 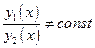 , то
, то  – есть общее решение этого уравнения.
– есть общее решение этого уравнения.
Для определения частных решений 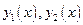 сотавляют характеристическоое уравнение:
сотавляют характеристическоое уравнение:  .
.
В зависимости от коэффициентов характеристическое уравнение может иметь либо 2 различных действительных корня, либо кратные корни, либо комплексные.
Не будем подробно рассматривать каждый случай, а сформулируем общее правило нахождения решения линейного однородного дифференциального уравнения с постоянными коэффициентами.
1) Составляем характеристическое уравнение и находим его корни.
2) Находим частные решения дифференциального уравнения, причем:
| Корни х.у. | Частные решения | Общее решение |
1. Действительные разные: 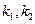
| 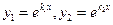
| 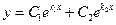
|
2. Равные 
| 
| 
|
3. Комплексные сопряженные: 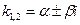
| 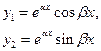
| 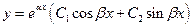
|
Пример. Решить уравнение 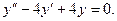
Характеристическое уравнение: 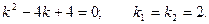
Общее решение: 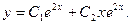
Пример. Решить уравнение 
Характеристическое уравнение: 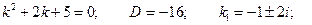
Общее решение: 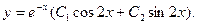
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.
Рассмотрим неоднородное уравнение 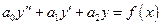 (1) с постоянными коэффициентами и с непрерывной правой частью. Уравнение с такими же коэффициентами, но правой частью равной нулю:
(1) с постоянными коэффициентами и с непрерывной правой частью. Уравнение с такими же коэффициентами, но правой частью равной нулю:
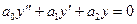 (2)
(2)
называется однородным уравнением, соответствующим неоднородному уравнению (1)
Теорема 1. Если известно какое-либо частное решение  неоднородного уравнения (1), то общее его решение
неоднородного уравнения (1), то общее его решение 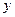 есть сумма этого частного решения и общего решения
есть сумма этого частного решения и общего решения  соответствующего однородного уравнения:
соответствующего однородного уравнения:  .
.
Теорема 2.
| Правая часть д.у. | Корни х.у. | Вид ч.р. |
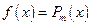 ,
где ,
где 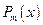 – многочлен степени – многочлен степени 
| а) число 0 не является корнеми х.у. |  , где , где  – многочлен степени не выше – многочлен степени не выше 
|
б) число 0 является корнеми х.у. кратности 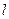
| 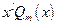
| |
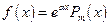 , ,
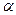 – вещественное число – вещественное число
| а) число 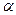 не является корнеми х.у. не является корнеми х.у.
| 
|
б) число 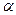 является корнеми х.у. кратности является корнеми х.у. кратности 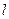
| 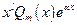
| |
  – многочлены степени не выше – многочлены степени не выше  и хоть один степени и хоть один степени 
| а) число  не является корнеми х.у. не является корнеми х.у.
| 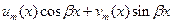 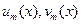 – многочлены степени не выше – многочлены степени не выше 
|
б) число  является корнеми х.у. кратности является корнеми х.у. кратности 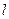
| 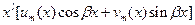
| |
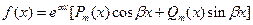
| а) число 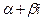 не является корнеми х.у. не является корнеми х.у.
| 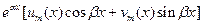
|
б) число 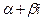 является корнеми х.у. кратности является корнеми х.у. кратности 
| 
|
Пример. Решить уравнение 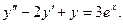
Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:
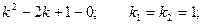
Общее решение однородного уравнения: 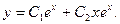
Теперь найдем частное решение неоднородного уравнения в виде:
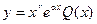
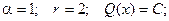
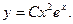
Воспользуемся методом неопределенных коэффициентов.
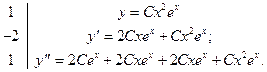
Подставляя в исходное уравнение, получаем:
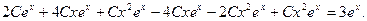
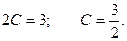
Частное решение имеет вид: 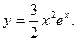
Общее решение линейного неоднородного уравнения: