События и их вероятности

Прежде чем приступить к решению первой задачи рекомендуется внимательно изучить понятия, теоремы и формулы, связанные с событиями. Для этого можно воспользоваться учебником по теории вероятностей (см. Библиографический список). Кроме того, полезно разобрать примеры 1- 4, приведенные ниже

Пример 1. Бросаются две игральные кости. Найти вероятность того, что сумма выпавших очков будет больше десяти.

Решение. Обозначим А событие – появление более десяти очков, Е_ij – событие, состоящее в том, что на первой кости выпадает i очков, а на второй j (i,j= 1,2,…,6). События Е_ij попарно несовместны, равновозможны, появление одного из них – событие достоверное. А это означает, что они образуют пространство элементарных событий Ω, позволяющее использовать классическое определение вероятности:

P (A)= .

Число элементов Ω равно n = 6∙6 = 36, из них благоприятствуют событию А – появлению более десяти очков (являются его частью, влекут) всего 3 (Е ₅₆, Е ₆₅, Е ₆₆) и, следовательно,

P (A)= = = ≈ 0,08.

Пример 2.. На полке расставлены 15 учебников, причем 5 из них в жестком переплете. Библиотекарь берет наугад три учебника. Найти вероятность того, что хотя бы один из них окажется в жестком переплете.

Решение. Обозначим события:

А - хотя бы один учебник в жестком переплете;

А ₁- один учебник в жестком переплете, два в мягком переплете;

А ₂- два учебника в жестком переплете, один в мягком;

А ₃ – все три учебника в жестком переплете.

По определению суммы событий искомое событие

А = А ₁ + А ₂ + А ₃.

События А ₁, А ₂, А₃ несовместны, следовательно,

 

P (A) = P(A ₁ + A ₂ + A ₃) = P (A ₁) + P (A ₂) + P (A ₃).

 

Для вычисления каждой из вероятностей событий А_j (j = 1,2,3) можно применить формулу классической вероятности, так как возможность взять любую из пятнадцати книг одинакова.

При определении общего числа элементов пространства элементарных событий и числа элементов, благоприятствующих исследуемому событию, используются элементы комбинаторики. Пространство элементарных событий будут образовывать неупорядоченные последовательности книг, отличающиеся друг от друга хотя бы одной книгой. Число таких последовательностей вычисляется как число сочетаний (читается «число сочетаний из r элементов по k элементов»). Оно может быть вычислено, в частности, по формуле

.

Напомним, что 0!=1.

В решаемой задаче r = 15 (общее число книг). При вычислении общего числа элементов пространства элементарных событий k =3 (выбираются наудачу три книги), т.е.

n = .

 

Определим число элементов, благоприятствующих событию А ₁: один учебник в переплете можно выбрать только из учебников в переплете, т.е. способами; два учебника без переплета выбираются из 10 учебников без переплета, т.е. способами; и поскольку к любой из книг может присоединиться любая из пар книг, общее число возможных последовательностей m ₁= . Таким образом,

P (A ₁)= = = .

 

Рассуждая аналогичным образом, получим

P (A ₂)= = = ;

P (A ₃)= = = .

 

Окончательно

P (A)= P (A ₁) + P(A ₂) + P(A ₃) = + + = » 0,736.

 

Однако существует более простое решение этой задачи.

Обозначим В – ни одна взятая книга не оказалась в жестком переплете. Это событие противоположно событию А – хотя бы одна книга в жестком переплете (В = или А = ). Поэтому

Р (А) = Р () = 1 – Р (В).

 

Р (В) = = = .

 

Тогда Р (А) = 1- = » 0,736.

Естественно, результат оказался таким же. Заметим, что существуют и другие способы решения этой задачи, зависящие от выбора пространства элементарных событий.

Пример 3. Стрелок производит шесть выстрелов по мишени с вероятностью попадания при каждом выстреле 0,7. Для выхода в следующий этап соревнований нужно иметь не меньше четырех попаданий. Найти вероятность выхода стрелка в следующий этап.

Решение. Обозначим А – стрелок вышел в следующий этап, А_i – стрелок попал i раз (i = 0, 1, …, 6). Стрелок должен попасть 4, 5 или 6 раз, т.е. А = А ₄ + А ₅ + А ₆. В силу несовместности событий А_i получим

P (A) = P(A ₄ + A ₅ + A ₆) = P (A ₄) + P (A ₅) + P (A ₆).

Найдем вероятности событий A_i. Вероятность того, что стрелок попадет в цель ровно i раз, следует вычислять исходя из того, что серия опытов образует схему Бернулли, т.е. по формуле

Р (A_i) = pⁱ q^6-i,

где q = 1- p, i = 0,1,2,…6.

 

Таким образом,

Р (А) = p ⁴ q ² + p ⁵ q + p ⁶ = 15·0.7⁴·0.3² + 6·0.7⁵·0.3 + 0.7⁶ » 0.324 + 0.303 + 0.118 » 0,745.

 

Пример 4. Из четырех купленных билетов лотереи, каждый может быть как выигрышным, так и проигрышным. Найти вероятность того, что наудачу взятый билет окажется выигрышным, если количество таких билетов среди купленных равновероятны. Найти вероятность того, что если взят выигрышный билет, то и все остальные оказались такими же.

Решение. Пусть событие А – взят выигрышный билет. Обозначим через В_k событие: «k билетов выигрышные», k = 0, 1, 2, 3, 4. Эти события «предшест-вуют» событию А и могут рассматриваться как гипотезы. Поскольку все они равновероятны, их вероятности

P (B_k) = = 0,2.

Вероятность события А вычисляется по формуле полной вероятности

 

Р (А) = ,

 

где Р ()– условная вероятность события А при условии, что событие B_i произошло. Для решаемой задачи эта формула примет вид

Р (А)= Р (В ₀) P (A / B ₀) + Р (В ₁) P (A / B ₁) + Р (В ₂) P (A/ B ₂) + Р (В ₃) P (A / B ₃) + + + + Р (В ₄) P (A / B ₄).

Вычислим условные вероятности появления выигрышного билета, если произошло событие B_i:

P (A / B ₀) = 0, так как среди билетов нет ни одного выигрышного,

P (A / B ₁) = , так как среди четырех билетов один выигрышный.

Соответственно

P (A / B ₂) = = ; P (A / B ₃) = ; P(A / B ₄) = 1.

Подставив найденные вероятности в формулу полной вероятности, получим

Р (А)= 0.2·0 + 0.2· + 0.2· + 0.2· + 0.2·1 = 0,5.

 

Переоценим доопытные, априорные, вероятности количества выигрышных среди купленных билетов после взятия выигрышного билета. Для этого воспользуемся формулой Байеса.

P(H_j/A) = ,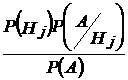

где H_j – гипотезы, «предшествующие» событию А. Учитывая, что в задаче H_j = В ₄, получим

 

P (H ₄/ A) = = = 0,4.

 

Таким образом, вероятность того, что все купленные билеты оказались выигрышными увеличилась в два раза.

Случайные величины

Перед решением задач по этой теме следует усвоить основные понятия, связанные со случайными величинами: дискретные и непрерывные случайные величины, законы их распределения; изучить примеры распределений; оценить роль числовых характеристик случайных величин.

Кроме того, следует разобрать приведенные ниже примеры 5 – 8.

 

Пример 5. Плотность вероятности случайной величины

f (x)=

Показать, что предложенная функция может быть плотностью вероятности некоторой случайной величины h. Найти её функцию распределения F (x), математическое ожидание M [h], дисперсию D [h], среднее квадратическое отклонение s_h и вероятность попадания случайной величины в интервал [1,3]. Построить графики плотности вероятности и функции распределения.

Решение. Покажем, что данная f(х) может быть плотностью вероятности.

Действительно, прежде всего, f(х) ³0. Проверим выполнение свойства

Следовательно, предложенную функцию можно рассматривать как плотность вероятности.

Найдем функцию распределения F (x) из соотношения

F (x)= .

Для х Î (-∞;0) F (x)= ,

для х Î [0;5] F (x)=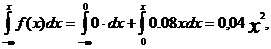

для х Î (5;+∞) F (x)= .

Окончательно: F (x)=

 

Построим графики плотности вероятности и функции распределения (рис. 1).

Рис. 1.

 

M [h]=

Для вычисления D [h], воспользуемся её свойством

D [h]= M [h²] - (M [h])² =

=

Cреднее квадратическое отклонение

s_h= = .

Вероятность попадания в интервал [1,3] можно вычислить любым из двух способов, используя либо плотность вероятности, либо функцию распределения.

В первом случае

P (1£h£3) = .

Во втором случае –

P (1£h£3) = F (3)- F (1)= 0.04×3²- 0.04×1²=0.32.

 

Пример 6. Функция распределения случайной величины h

 

F(x)=

Показать, что эта функция может быть функцией распределения некоторой непрерывной случайной величины; найти её плотность вероятности f (x), математическое ожидание M [h], дисперсию D [h], среднее квадратическое отклонение s_h, построить графики функции распределения и плотности вероятности; найти вероятность попадания в интервал .

Решение. Чтобы F(x) могла быть функцией распределения непрерывной случайной величины она, во-первых, должна быть определена на всей числовой оси. Действительно, F(x) определена на интервалах , и в точках границ интервалов односторонние пределы функции равны её значениям. Во-вторых, её область значений должна быть [0;1]. Действительно, все значения F (x) принадлежат интервалу [0,1], (0 так как sin xÎ [-1;1]).

И, наконец, F (x)=0, F (x)=1.

Из всего сказанного следует, что предложенная функция может быть функцией распределения непрерывной случайной величины.

Плотность вероятности найдем из соотношения f (x)= F ¢(x). Заметим, что F (x) задана разными выражениями в области её определения, следовательно, и f (x) также будет описана разными выражениями на этих интервалах

 

f (x) =

Построим графики f (x) и F (x) (рис. 2)

Рис. 2

Найдем математическое ожидание:

M [h]= .

Найдем дисперсию:

D [h]=

=

 

=