Если функция  является аналитической в замкнутой односвязной области D, то интеграл от нее по любому замкнутому контуру, расположенному в области D, равен нулю:
является аналитической в замкнутой односвязной области D, то интеграл от нее по любому замкнутому контуру, расположенному в области D, равен нулю:  .
.
Доказательство:
Пусть функция  аналитическая в области D. Тогда для нее выполняютcя условия Коши-Римана (1.19)
аналитическая в области D. Тогда для нее выполняютcя условия Коши-Римана (1.19)

| (1.25) |
Вспомним условие равенства нулю криволинейного интеграла второго рода  по любому замкнутому контуру
по любому замкнутому контуру
 , ,
| (1.26) |
тогда первое условие (1.19) обращает в ноль второй интеграл в правой части равенства (1.25), а второе условие (1.19) – первый. Что и требовалось доказать.
Можно доказать, что для аналитической функции интеграл по контуру зависит только от начальной и конечной точек интегрирования. Более того, для аналитической функции имеет место формула Ньютона-Лейбница
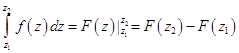 , ,
| (1.27) |
где  - первообразная аналитической функции
- первообразная аналитической функции  .
.
Пример 1.23
Вычислить интеграл  .
.
Решение
Подынтегральная функция  является аналитической. Воспользуемся формулой Ньютона-Лейбница (1.27), получим
является аналитической. Воспользуемся формулой Ньютона-Лейбница (1.27), получим
 .
.
Задачи для самостоятельного решения
| Задания | Ответы | |
 , найти , найти 
| 
| |
 , найти , найти 
| 
| |
 , найти , найти 
| 
| |
Найти 
| ||
Найти 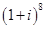
| ||
Какая линия описывается уравнением
 ? ?
| Окружность с центром в начале координат и радиусом 2 | |
Найти 
| 
| |
Вычислить 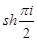
| 
| |
Вычислить 
| 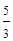
| |
Решить уравнение 
| 
| |
Какие из функций являются аналитическими
а)  ; б) ; б)  ; в) ; в)  ? ?
| Только в) | |
Решить уравнение 
| 
|
Глава 2
Элементы операционного исчисления
Оригиналы и изображения. Преобразование Лапласа.
Функцией-оригиналом называется функция  , удовлетворяющая следующим трем условиям:
, удовлетворяющая следующим трем условиям:
1.  – непрерывна или имеет конечное число точек разрыва первого рода на каждом конечном интервале.
– непрерывна или имеет конечное число точек разрыва первого рода на каждом конечном интервале.
2. Существуют такие числа М и  , что
, что  .
.
Это неравенство означает, что  может расти не быстрее экспоненциальной функции
может расти не быстрее экспоненциальной функции  . Например,
. Например,  – не является оригиналом.
– не является оригиналом.
3.  , для всех
, для всех  .
.
Первые два условия часто выполняются в практических задачах. Чтобы выполнялось третье условие, используется функция

| (2.1) |
которая называется функцией Хевисайда.
Все функции-оригиналы  в операционном исчислении считаются умноженными на множитель Хевисайда
в операционном исчислении считаются умноженными на множитель Хевисайда 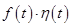 . Однако этот множитель, как правило, не записывается, а только подразумевается.
. Однако этот множитель, как правило, не записывается, а только подразумевается.
Функция 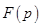 называется изображением функции
называется изображением функции  , если они связаны соотношением
, если они связаны соотношением

| (2.2) |
Правая часть (2.2) – преобразование Лапласа для функции  , а сам интеграл называется интегралом Лапласа; p – комплексный параметр. Тот факт, что
, а сам интеграл называется интегралом Лапласа; p – комплексный параметр. Тот факт, что 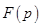 является изображением функции
является изображением функции  , символически записывается в виде
, символически записывается в виде  или
или  =
= 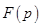 , L – оператор Лапласа:
, L – оператор Лапласа:
 .
.
Пример 2.1
Найдем изображение 1 или функции Хевисайда  , определенной равенством (2.1).
, определенной равенством (2.1).
 или
или  .
.
 .
.
Таким образом, получили изображение функции Хевисайда или изображение единицы:

| (2.3) |
Пример 2.2
Найдем изображение функции  .
.
 .
.
 . .
| (2.4) |
Свойство линейности
Пусть  и
и  , тогда
, тогда

| (2.5) |
Это свойство является следствием линейности оператора Лапласа, т.е. следствием линейности определенного интеграла.
Пример 2.3
 .
.
Таким образом,

| (2.6) |
Аналогично можно получить изображение

| (2.7) |
Задание.
Найти изображения функций: 1)  , 2)
, 2)  .
.
Ответы: 1)  ; 2)
; 2)  .
.
Свойство подобия
Пусть  , тогда
, тогда
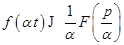 , ,
| (2.8) |
Доказательство.
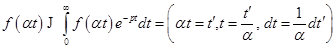 =
=
= 
Пример 2.4
Используя формулы (2.6) и (2.8) Найдем изображение функции  .
.
 .
.
Таким образом,

| (2.9) |