Линейные операции над геометрическими векторами:

1. Линейными операциями над векторами называют операции сложения, вычитания и умножения вектора на число.

2. Суммой двух свободных векторов а и b таких, что начало вектора b совпадает с концом вектора а называется вектор с=а+b, соединяющий начало первого вектора с концом второго вектора (правило треугольника).

3. Суммой двух свободных векторов а и b, приведённых к одному началу, называется вектор с=а+b, имеющий общее начало с векторами а, b и совпадающий с диагональю параллелограмма, построенного на этих векторах.

4. Разностью двух свободных векторов а и b называется вектор с=а-b такой, что b+с=а.

5. Произведение вектора а на число α называется вектор α×а или а×α, который имеет длину │α│×│а│, коллениарен вектору а, имеет направление вектора а, если α>0, и противоположное направление, если α<0.

Линейные операции над векторами. Основные задачи.

1. Сумма двух свободных векторов а и b: а+b=(а₁+b₁;a₂+b₂;a₃+b₃)

2. Разность двух свободных векторовa и b: а-b=(a₁-b₁;a₂-b₂;a₃-b₃).

3. Произведение вектора а на число α: αа=(αа₁;αа₂;αа₃)

4. Свойства линейных операций над векторами:

· a+b=b+a

· (a+b)+c=a+(b+c)

· α₁(α₂×a)=α₁×α₂×a

· (α₁+α₂)×a=α₁×a+α₂a

· α(a+b)=αa+αb

№4 Скалярное произведение векторов и его свойства.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними а×b=│a│×│b│×cosα. Если хотя бы один из векторов равен нулю или косинус угла(векторы перпендикулярны), то скалярное произведение равно нулю.

1. a×b=b×a – переместительное свойство

2. (αa)b=α(ab) – сочетательное свойство относительно скалярного множителя

3. a(b+c)=ab+ac – распределительное свойство

4. Скалярный квадрат вектора равен квадрату его длины а²=│а│²

5. I²=j²=k²=1

6. √a²=│a│

7. Если а=a_xi+a_yj+a_zk, b=b_xi+b_yj+b_zk, то скалярное произведение равно сумме произведений их одноимённых координат: а×b=a_xb_x+a_yb_y+a_zb_z

8. Угол α между ненулевыми векторами а=(a_x;a_y;a_z) и b=(b_x;b_y;b_z) (здесь надо от руки переписать формулу со шпаргалки)

9. Длина вектора находится по формуле

10. d = \/(х₂— х₁)² + (y₂— y₁)² - Полученная формула позволяет находить расстояние между любыми двумя точками плоскости

№9 Общее уравнение прямой на плоскости и его исследование.

, A²+B²≠0 - общее уравнение прямой, (для общего уравнения прямой угловой коэффициент высчитывается по формуле k=-A/B, а b= -C/B).

- уравнение прямой с угловым коэффициентом, 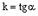- угловой коэффициент прямой равен тангенсу угла наклона этой прямой к оси ОХ, b-величина отрезка, отсекаемого прямой на оси Оy).

Если две прямые заданы уравнениями с угловым коэффициентом y = k ₁ x + B ₁, y = k ₂ x + B ₂, то угол между ними определяется по формуле =

Признаком параллельности двух прямых является равенство их угловых коэффициентов:

Признаком перпендикулярности двух прямых является соотношение:

Уравнение прямой, проходящей через данную точку М(х₀,у₀) (уравнение пучка прямых) у-у₀=к(х-х₀).

Уравнение прямой, проходящей через две заданные точки М₁(х₁,у₁), М₂(х₂,у₂) = , Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле К= .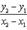

Прямая линия, пересекающая ось Ox в точке (а;0) и ось Oy в точке (0;b): - уравнение прямой в отрезках (в этом виде невозможно представить прямую, проходящую через начало координат).

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу. (для Ах+Ву+С=0). Угловой коэффициент прямойпоказывает какой угол образует прямая с осью ОХ.

№12 Гипербола и её каноническое уравнение

Гипербола – множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. (│r₁-r₂│=2a, 2a<2c

- каноническое уравнение гиперболы

- эксцентриситет гиперболы, где а - расстояние от центра гиперболы до ее вершины. Центр гиперболы О(0;0), Точки А₁(а;0), А₂(-а;0) – вершины гиперболы. а – действительная полуось, b – мнимая полуось; Фокусы гиперболы – точки: F₁(-c;0) и F₂(c;0), (с²=а²+b²).

Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам: , , Фокальные радиусы точек левой ветви вычисляются по формулам: ,

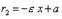
Асимптоты гиперболы: ,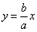

Директрисы гиперболы: ,

если r - расстояние от произвольной точки гиперболы до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету гиперболы:

№13 Определение параболы и её каноническое уравнение

Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Каноническое уравнение параболы с параметром р>0: у²=2рх

Ось Ох – ось симметрии параболы, О(0;0) –может быть вершиной параболы. Фокус параболы – точка F(p/2;0). Уравнение директрисы х= -р/2. Фокальный радиус точки М(х;у) параболы: r=x+p/2