Задачи теории игр
Если имеется несколько конфликтующих сторон (лиц), каждая из которых принимает некоторое решение, определяемое заданным набором правил, и каждому из лиц известно конечное состояние конфликтной ситуации с заранее определенными для каждой из сторон платежами, то говорят, что имеет место игра.
Задача теории игр состоит в выборе такой линии поведения данного игрока, отклонение от которой может лишь уменьшить его выигрыш.
Некоторые определения игры
Количественная оценка результатов игры называется платежом.
Парная игра (два лица) называется игрой с нулевой суммой, если сумма платежей равна нулю, т.е. если проигрыш одного игрока равен выигрышу другого.
Однозначное описание выбора игрока в каждой из возможной ситуаций, при которой он должен сделать личный ход, называется стратегией игрока.
Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает игроку максимально возможный средний выигрыш (или, что - то же самое, минимально возможный средний выигрыш).
Игра, определяемая матрицей А, имеющей m строк и n столбцов, называется конечной парной игрой размерности m*n;
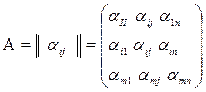 (1.1)
(1.1)
где i =  - стратегия первого игрока, имеющего m стратегий; j =
- стратегия первого игрока, имеющего m стратегий; j = 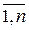 - стратегия второго игрока, имеющего n стратегий;
- стратегия второго игрока, имеющего n стратегий;  ij – выигрыш первого игрока по i -й стратегии при использовании вторым j -й стратегии (или, что то же самое, проигрыш второго по своей j -й стратегии, при использовании первым i -й);
ij – выигрыш первого игрока по i -й стратегии при использовании вторым j -й стратегии (или, что то же самое, проигрыш второго по своей j -й стратегии, при использовании первым i -й);
А = || a ij || – платежная матрица игры.
1.1 Игра с чистыми стратегиями
Нижняя цена игры (для игрока первого)
a = max (min a ij). (1.2)
i j
Верхняя цена игры (для второго игрока):
 = min (maxaij). (1.3)
= min (maxaij). (1.3)
J i
Если a = b, игра называется с седловой точкой (1.4), или игра с чистыми стратегиями. При этом V = a = b называют ценной игры (V - цена игры).
Пример. Дана платежная матрица игры 2 лиц А. Определить оптимальные стратегии для каждого из игроков и цену игры:
min max
j i
 (1.4)
(1.4)
 max 10 9 12 6
max 10 9 12 6
i
min 6
j
 - стратегия первого игрока (строки).
- стратегия первого игрока (строки).
 - стратегия второго игрока (столбцы).
- стратегия второго игрока (столбцы).
 - цена игры.
- цена игры.
Таким образом, игра имеет седловую точку. Стратегия j = 4 – оптимальная для второго игрока, стратегия i =2 - для первого. Имеем игру с чистыми стратегиями.
1.2 Игры со смешанными стратегиями
Если платежная матрица не имеет седловой точки, т.е.  , и ни один из участников игры не может выбрать один план в качестве своей оптимальной стратегии, игроки переходят на «смешанные стратегии». При этом каждый из игроков использует в процессе игры несколько раз каждую из своих стратегий.
, и ни один из участников игры не может выбрать один план в качестве своей оптимальной стратегии, игроки переходят на «смешанные стратегии». При этом каждый из игроков использует в процессе игры несколько раз каждую из своих стратегий.
Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока.
Х = (х1…хi…хm) – смешанная стратегия первого игрока.
У = (у1…уj…уn) – смешанная стратегия второго игрока.
 xi, уj – относительные частоты (вероятности) использования игроками своих стратегий.
xi, уj – относительные частоты (вероятности) использования игроками своих стратегий.
Условия использования смешанных стратегий
 . (1.5)
. (1.5)
Если Х * = (х 1*…. х i*… хm *) – оптимальная стратегия, выбранная первым игроком; Y * = (у 1*… у j*… уn *) – оптимальная стратегия, выбранная вторым игроком, то число является ценой игры.
 (1.6)
(1.6)
Для того чтобы число V было ценой игры, а х * и у * - оптимальными стратегиями, необходимо и достаточно выполнение неравенств
 (1.7)
(1.7)
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры V вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную, в том числе и чистые стратегии.
Сведения задач теории игр к задачам линейного программирования.
Пример. Найти решение игры, определяемой платежной матрицей А.
А = 
 (1.8)
(1.8)
y 1 y 2 y 3
Решение:
Составим двойственную пару задач линейного программирования.
Для первого игрока
 (1.9)
(1.9)
у 1 + у 2 + у 3 = 1 (1.10)
Освобождаясь от переменной V (цена игры), разделим левую и правую часть выражений (1.9), (1.10) на V. Приняв уj / V за новую переменную zi, получим новую систему ограничений (1.11) и целевую функцию (1.12)
 (1.11)
(1.11)
 . (1.12)
. (1.12)
Аналогично получим модель игры для второго игрока:
 (1.13)
(1.13)
х 1 + х 2 + х 3 = 1. (1.14)
Приведя модель (1.13), (1.14) к форме без переменной V, получим
 (1.15)
(1.15)
 , (1.16)
, (1.16)
где  .
.
Если нам необходимо определить стратегию поведения первого игрока, т.е. относительную частоту использования его стратегий (х 1…. хi…хm), мы будем использовать модель второго игрока, т.к. эти переменные находятся в его модели выигрыша (1.13), (1.14).
Приведем (1.15), (1.16) к канонической форме
 (1.17)
(1.17)
 . (1.18)
. (1.18)
Дальше задача (1.17), (1.18) решается симплекс – методом (табл.1.1)
Базисное решение:
d 1 = 1/2; d 2 = 1/2; d 3 = 0; d 4 = 0; d 5 = 0; d 6 = 0.
Цена игры:

Исходные параметры, относительные частоты применения стратегий

x 3 = 0; x 4 = 0; x 5 = 0; x 6 = 0;
x 2 = d 2 × V = 1/2×1 = 1/2.
Для проведения стратегий второго игрока используется модель игры первого: (1.9), (1.10), (1.11), (1.12).
Таблица 1.1
| Б | d 1 d 2 d 3 d 4 d 5 d 6 | св. чл | bj / aij |
| d 4 1 d 5 d 6 | 1 1 3 1 0 0
 2 0 2 0 1 0
0 2 1 0 0 1 2 0 2 0 1 0
0 2 1 0 0 1
| I I I | 1/2 |

|  -1 -1 -1 0 0 0 -1 -1 -1 0 0 0
| ||
| d 4 2 d 5 d 2 | 1 0 5/2 1 0 -1/2 2 0 2 0 1 0 0 1 1/2 0 0 1/2 | 1/2 1/2 | 1/2 |

| -1 0 -1/2 0 0 1/2 | 1/2 | |
| d 1 3 d 5 d 2 | 1 0 5/2 1 0 -1/2 0 0 -3 -2 1 1 0 1 1/2 0 0 1/2 | 1/2 1/2 | |

| 0 0 2 1 0 0 |
2 Графический метод
Графическое решение может быть использовано, когда один из игроков имеет только два возможных плана игры. Проиллюстрируем это на примере:
x1 x2 x3

Нам необходимо определить стратегии первого игрока. Предположим, что он выигрывает. Для этого составим модель проигрыша второго:
 (2.1)
(2.1)
 (2.2)
(2.2)
 (2.3)
(2.3)
 (2.4)
(2.4)
Заменим  в неравенствах (2.1)-(2.3):
в неравенствах (2.1)-(2.3):
 (2.5)
(2.5)
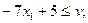 (2.6)
(2.6)
 (2.7)
(2.7)
Построим прямые в интервале  .
.
 (2.8)
(2.8)
 (2.9)
(2.9)
 (2.10)
(2.10)
как показано на рис. 1.



И выделим область, удовлетворяющую условиям (2.5) - (2.7) − область допустимых решений. На этой области выбирается точка v, которая имеет наибольшее значение (точка А). Координаты этой точки находятся совместным решением уравнений (2.8) и (2.9):
 ,
,



Отсюда

т.е. цена игры 
3 Аналитический метод
Пример: y1 y2
 .
.
Определить стратегии поведения игрока и цену игры. Составляем модели выигрыша (проигрыша) для каждого игрока.
Игрок А: Игрок В:
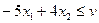 , (3.1)
, (3.1)  , (3.7)
, (3.7)
 , (3.2)
, (3.2)  , (3.8)
, (3.8)
 . (3.3)
. (3.3)  . (3.9)
. (3.9)
Запишем модели в виде уравнений:
 , (3.4)
, (3.4)  , (3.10)
, (3.10)
 , (3.5)
, (3.5)  , (3.11)
, (3.11)
 .
.  .
.
Начнем решение с игрока А. Исключим цену игры v:
 ,
,
 . (3.6)
. (3.6)
Решим совместно уравнения (3.3) и (3.6):
 ,
,
 ,
,


Подставим эти значения в уравнения (3.4) и (3.5), получим:

Для игрока В подставим v в одно из уравнений (3.10) или (3.11) и решим совместно с уравнением (3.9).

Получим: 

Игры с «природой»
В рассмотренных выше матричных играх предполагалась, что в них принимают участие два игрока, интересы которых противоположны. Поэтому действия каждого игрока направлены на увеличение выигрыша (уменьшение проигрыша). Однако в некоторых задачах, приводящихся к игровым, имеется неопределенность, вызванная отсутствием информации об условиях, в которых осуществляется действие (погода, покупательский спрос и т.д.). Эти условия зависят не от сознательных действий игроков, а от объективной действительности. Такие игры называются играми с «природой». Человек в играх с природой старается действовать осмотрительно, второй игрок (природа, покупательский спрос) действует случайно.
Условия игры задаются матрицей  .
.
Имеется ряд критериев, которые используются при выборе оптимальной стратегии. Рассмотрим некоторые из них.
1. Критерий Байеса – Лапласа.
Критерием принятия решений является максимум математического ожидания, т.е. 
2. Критерий Лапласа.
Здесь предполагают, что все состояния природы равновероятны, т. е.  , т.е.
, т.е.  .
.
3. Максимальный критерий Вальда.
Рекомендуется применять максиминную стратегию, т. е. 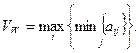 Критерий является пессимистичным, считается, что природа будет действовать наихудшим для человека образом.
Критерий является пессимистичным, считается, что природа будет действовать наихудшим для человека образом.
4. Критерий минимального риска Сэвиджа.
Суть критерия состоит в выборе такой стратегии, чтобы не допустить чрезмерно высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии. Элемент матрицы рисков  находится по формуле
находится по формуле  , где
, где  Оптимальная стратегия находится из выражения
Оптимальная стратегия находится из выражения 
5. Критерий Гурвица.
Критерий рекомендует стратегию, определяемую по формуле  Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего для человека поведения природы. При
Критерий придерживается некоторой промежуточной позиции, учитывающей возможность как наихудшего, так и наилучшего для человека поведения природы. При  критерий превращается в критерий Вальда. На
критерий превращается в критерий Вальда. На  оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем хуже последствия ошибочных решений, больше желания застраховаться, тем
оказывает влияние степень ответственности лица, принимающего решение по выбору стратегии. Чем хуже последствия ошибочных решений, больше желания застраховаться, тем  ближе к единице.
ближе к единице.
Пример. Возможно строительство четырех типов электростанций: тепловых (стратегия А1), приплотинных (стратегия А2), бесшлюзовых (стратегия А3), шлюзовых (стратегия А4). Эффективность каждого из типов зависит от различных факторов: режима рек, стоимости топлива и его перевозки и т. п.. Предположим, что выделено четыре различных состояния, каждое из которых означает определенное сочетание факторов, влияющих на эффективность энергетических объектов. Состояния природы обозначим через Р1, Р2, Р3, Р4. Экономическая эффективность строительства отдельных видов электростанций изменяется в зависимости от состояний природы и задана матрицей. Проанализировать ситуацию и выбрать оптимальную стратегию (по критерию Байеса – Лапласа, Лапласа, Вальда, Сэвиджа, Гурвица).

Решение.
По критерию Байеса –Лапласа. Определим математическое ожидание выигрыша статистика при выборе им стратегии Аi:
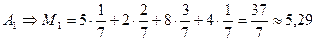



 .
.
В соответствии с этим критерием наиболее предпочтительными являются стратегии А1 и А2.
По критерию Лапласа.
Все состояния природы равновероятны, т. е. p1=p2=p3=p4=  .
.
 ;
; 


Используя критерий Лапласа, получаем  , то оптимальной является стратегия А3.
, то оптимальной является стратегия А3.
По критерию Вальда.
 Следовательно максимальная стратегия статистика - А3.
Следовательно максимальная стратегия статистика - А3.
По критерию Сэвиджа.
Построим матрицу рисков:  ,
,  В соответствии с этим критерием также наиболее предпочтительнее стратегия А3.
В соответствии с этим критерием также наиболее предпочтительнее стратегия А3.
По критерию Гурвица.
 Таким образом, согласно критерию Гурвица оптимальной стратегией является стратегия А2.
Таким образом, согласно критерию Гурвица оптимальной стратегией является стратегия А2.
Вывод: Анализ результатов, проведенных на основе различных критериев, показывает, что наиболее приемлемой является стратегия А3.
Задачи для самостоятельного решения
I ЗАДАНИЕ
Выбор варианта по последней цифре зачетной книжки.
Найдите нижнюю цену игры, верхнюю цену игры, определите седловые точки, оптимальные чистые стратегии и цену игры (если они существуют):
1.1  1.2
1.2 
1.3  1.4
1.4  1.5
1.5 
1.6  1.7
1.7  1.8
1.8 
1.9  1.10
1.10 
I I ЗАДАНИЕ
Выбор варианта по последней цифре зачетной книжки.
Решить графически игровые задачи:
1.  2.
2.  3.
3. 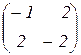 4.
4.  5.
5. 
6.  7.
7.  8.
8.  9.
9.  10.
10. 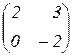
I I I ЗАДАНИЕ
Выбор варианта по последней цифре зачетной книжки
Оборудование после k работы может оказаться в одном из трех состояний: Q1 – оборудование вполне работоспособно и требует лишь небольшого текущего ремонта; Q2 – требуется серьезный капитальный ремонт; Q3 – дальнейшая эксплуатация оборудования невозможна. Вероятности этих событий q1, q2, q3 (таб. 6). Для предприятия возможны три стратегии: А1 – оставить оборудование в работе еще на год, проведя незначительный ремонт, А2 – провести капитальный ремонт, А3 – заменить оборудование. Потери, которые несет предприятие при различных стратегиях, даны в таблице:
| Q1 | Q2 | Q3 | |
| А1 | |||
| А2 | |||
| А3 |
Определить оптимальную стратегию, используя:
1) критерий Байеса – Лапласа;
2) максимальный критерий Вальда;
3) критерий минимального риска Сэвиджа;
4) критерий Гурвица статистика с заданным значением L=0,6.
| q1 | q2 | q3 | q1 | q2 | q3 | ||
| 0,5 | 0,3 | 0,2 | 0,5 | 0,4 | 0,1 | ||
| q1 | q2 | q3 | q1 | q2 | q3 | ||
| 0,4 | 0,4 | 0,2 | 0,3 | 0,5 | 0,2 | ||
| q1 | q2 | q3 | q1 | q2 | q3 | ||
| 0,2 | 0,6 | 0,2 | 0,1 | 0,7 | 0,2 | ||
| q1 | q2 | q3 | q1 | q2 | q3 | ||
| 0,5 | 0,1 | 0,4 | 0,5 | 0,4 | 0,1 | ||
| q1 | q2 | q3 | q1 | q2 | q3 | ||
| 0,6 | 0,3 | 0,1 | 0,4 | 0,3 | 0,3 | ||
| q1 | q2 | q3 | q1 | q2 | q3 | ||
| 0,3 | 0,3 | 0,4 | 0,2 | 0,3 | 0,5 | ||
| q1 | q2 | q3 | q1 | q2 | q3 | ||
| 0,1 | 0,3 | 0,6 | 0,3 | 0,4 | 0,3 |
IV ЗАДАНИЕ
Выбор варианта по последней цифре зачетной книжки.
Составить платежные матрицы и решить игры в задачах:
4.1 Каждый из двух участников игры, независимо один от другого, показывает на руке «камень», «бумагу» или «ножницы», при этом «бумага» выигрывает у «камня» одно очко, «камень выигрывает» у «ножниц» два очка, «ножницы» выигрывают у «бумаги» три очка. С какими вероятностями следует показывать каждому игроку указанные предметы, чтобы получить максимальный гарантированный выигрыш?
4.2 Игра заключается в том, что игрок А записывает числа 1 или 2, или 3, а игрок В, независимо от А записывает числа 1 или 2, или 3, или 4. если сумма двух чисел окажется четной, то А выигрывает эту сумму, если – нечетной, то В выигрывает сумму этих чисел. Составить платежную матрицу. Определить нижнюю и верхнюю цену игры, максиминную и минимаксную стратегии игроков.
4.3 Игрок А загадывает монету достоинством либо в 10 коп., либо в 20 коп. Если В отгадывает, то и получает ее. В противном случае В платит А 15 коп. Определить оптимальный способ ведения игры каждым игроком.
4.4 У стороны А имеется два объекта, но надежно оборонять от атак противника она может лишь один объект (для обороны двух объектов у нее не хватает сил). Сторона В может в данных условиях атаковать только один из двух объектов (для атаки двух объектов не хватает сил). Если А будет оборонять атакуемый объект, то атака будет отбита. Ценность одного объекта в 4 раза больше другого. Найти оптимальное поведение стороны А в обороне и стороны В в нападении.
 4.5 Предприятие может выпускать три вида продукции А1,А2, А3. Прибыль, получаемая предприятием, зависит от спроса на эту продукцию, который может принять одно из четырех состояний В1, В2, В3, В4. Элементы следующей матрицы характеризуют прибыль при выпуске продукции Ai и состоянии спроса Bk:
4.5 Предприятие может выпускать три вида продукции А1,А2, А3. Прибыль, получаемая предприятием, зависит от спроса на эту продукцию, который может принять одно из четырех состояний В1, В2, В3, В4. Элементы следующей матрицы характеризуют прибыль при выпуске продукции Ai и состоянии спроса Bk:
Определить оптимальные пропорции в выпускаемой продукции при условии, что состояние спроса предприятия не известно.
4.6 Предприятие выпускает скоропортящуюся продукцию, которую оно может сразу отправить потребителю (стратегия А1), отправить на склад на хранение (стратегия А2) или подвергнуть дополнительной обработке (стратегия А3) для длительного хранения. Потребитель может немедленно приобрести продукцию (стратегия В1), в течении небольшого промежутка времени (стратегия В2) и после длительного периода времени (стратегия В3). Элементы следующей матрицы характеризуют затраты, понесенные предприятием при применении пары стратегий Ai и Bk:

4.7 Случайно выбирается целое число z с возможными значениями 1,2,3,4. Игроки, независимо и не зная этого числа, записывают целые числа х и у. Выигрыш одного игрока у другого определяется по формуле | y - z | - | х - z | (цель каждого игрока - выбрать число, по возможности приближенное к z). Составить платежную матрицу. Найти наилучший способ ведения игры каждым игроком.
4.8 Игрок А имеет две карты («туз» и «двойка»); он наугад берет одну из них. Если оказался «туз» и игрок В ему верит, то он платит А 1 руб., если не верит, то он платит А 2 руб. Если оказалась «двойка», то игрок А имеет две возможности: не обмануть В (сказать, что у него «двойка»), тогда А платит В 1 руб., обмануть В (сказать, что у него «туз»), тогда у В имеются две возможности: проверить А и отдать 1 руб. и не поверить А. Тогда, если при проверке окажется, что А обманул В, то А платит В 2 руб., если окажется, что А не обманул В, то В платит А 2 руб. Составить матрицу игры. Найти оптимальные стратегии игроков.
4.9 Два игрока независимо друг от друга называют по одному числу из диапазона 1-5. Если сумма чисел нечетная, то игрок 2 платит игроку 1 сумму, равную максимальному из чисел; если четная, то платит игрок 1.
V ЗАДАНИЕ
Выбор варианта по последней цифре зачетной книжки.
Фирма изготавливает железобетонные панели, используя в качестве основного сырья цемент. В связи с неопределенным спросом на изделия потребность в сырье в течение месяца также не определена. Цемент поставляется в мешках, причем известно, что потребность может составлять D1, D2,…,Dn мешков.
Резервы сырья на складе могут составлять R1, R2,…,Rn мешков в месяц. Учитывая, что удельные затраты на хранение сырья равны с1, а удельные издержки дефицитности сырья (потери, связанные с отсутствием необходимого количества цемента на складе) равны с2.
Определить оптимальную стратегию управления запасами цемента на складе.
Варианты
| N | ||||||||||
| c1 | ||||||||||
| c2 | ||||||||||
| R1 | ||||||||||
| R2 | ||||||||||
| R3 | ||||||||||
| R4 | ||||||||||
| R5 | ||||||||||
| D1 | ||||||||||
| D2 | ||||||||||
| D3 | ||||||||||
| D4 | ||||||||||
| D5 |
VI ЗАДАНИЕ
Выбор варианта по двум последним цифрам зачетной книжки.
 Предприятие может выпускать три вида продукции А1,А2, А3, получая прибыль, зависящую от спроса на эту продукцию. Спрос, в свою очередь, может принимать одно из четырех состояний В1, В2, В3, В4. В матрице элементы аi k характеризуют прибыль, которую получает предприятие при выпуске продукции Аi и состоянии спроса Вk.
Предприятие может выпускать три вида продукции А1,А2, А3, получая прибыль, зависящую от спроса на эту продукцию. Спрос, в свою очередь, может принимать одно из четырех состояний В1, В2, В3, В4. В матрице элементы аi k характеризуют прибыль, которую получает предприятие при выпуске продукции Аi и состоянии спроса Вk.
Определить оптимальные пропорции в выпускной продукции, считая состояние спроса полностью неопределенным. Гарантируя при этом среднюю величину прибыли при любом состоянии спроса.
С этой целью необходимо представить задачу как матричную игру двух лиц (предприятие - спрос) с нулевой суммой. Исключить заведомо невыгодные стратегии игроков, найти оптимальные стратегии и цену игры сведением игры к паре симметричных двойственных задач линейного программирования. Определить оптимальные пропорции в выпускаемой продукции.
Таблица 7.1
Выбор варианта
| № | а11 | а12 | а13 | а14 | а21 | а22 | а23 | а24 | а31 | а32 | а33 | а34 |