Тема 14. Методы интегрирования
Приведем основные методы вычисления неопределенного интеграла.
Метод замены переменной
Его использование базируется на следующей «цепочке» равенств:

где F (t) первообразная функции f (t). Далее необходимо подставить вместо t выражение g(x).
Метод подстановки
Описывается равенством
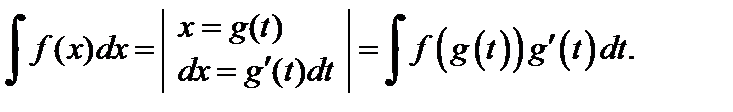
Этот метод используют в том случае, если последний интеграл вычисляется проще чем заданный.
Метод поднесения под знак дифференциала
Для вычисления интеграла используют определение дифференциала:
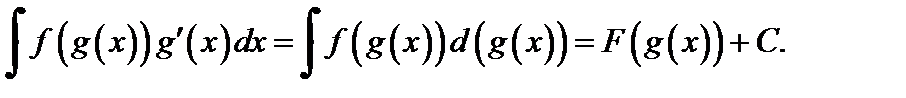
Согласно этому методу не делают явно замену переменной, подразумевая, что g (x) играет роль новой независимой переменной.
При использовании метода поднесения под знак дифференциала, метода замены переменной, метода подстановки удобно использовать простейшие преобразования дифференциала:
1) 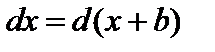 (b – произвольная постоянная величина);
(b – произвольная постоянная величина);
2)  (постоянная
(постоянная  );
);
3)  (постоянная
(постоянная 
Пример 1. Найти неопределенный интеграл:
1)  2)
2) 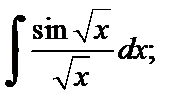 3)
3)  4)
4) 
Решение. 1) 1-й способ. Используем метод замены переменной. Положим 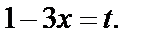 Тогда
Тогда 
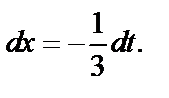 Имеем:
Имеем:

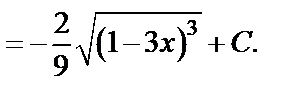
Для вычисления интеграла использовали формулу таблицы неопределенных интегралов.
2-й способ. Используем метод поднесения под знак дифференциала. Представим данный интеграл в следующем виде:
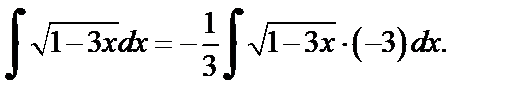
Учитывая, что  по формуле таблицы неопределенных интегралов получаем:
по формуле таблицы неопределенных интегралов получаем:


2) Поскольку  то
то  Поднесение под дифференциал приводит далее к интегралу
Поднесение под дифференциал приводит далее к интегралу 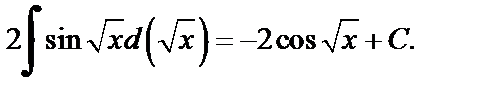
Для вычисления интеграла использовали формулу таблицы неопределенных интегралов.
3) Очевидно, что  Значит,
Значит,

Применяя формулу таблицы интегралов, получаем ответ: 
4) Используя второе свойство неопределенного интеграла, представим заданный интеграл в виде суммы двух интегралов:
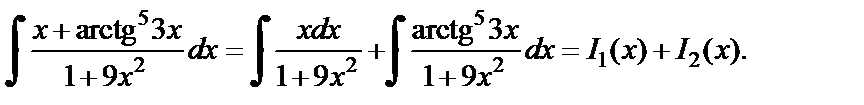
Вычислим полученные интегралы отдельно. Так как  то, используя далее формулу таблицы интегралов, получаем:
то, используя далее формулу таблицы интегралов, получаем:

Так как 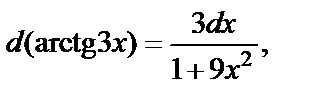 то по формуле таблицы интегралов имеем:
то по формуле таблицы интегралов имеем:
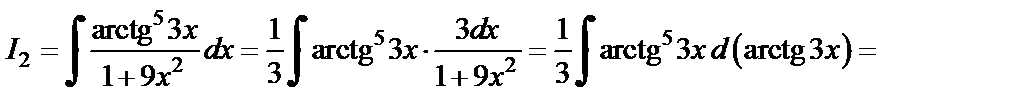
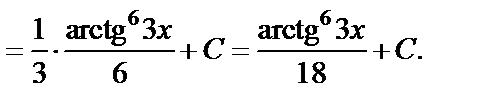
Подставив найденные значения интегралов I 1(x) и I 2(x) в первоначальный интеграл, приходим к ответу: 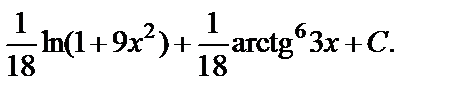
Пример 2. Методом подстановки найти интеграл:
1)  2)
2)  3)
3) 
Решение. 1) Используем метод подстановки. Положим 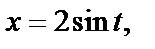 тогда
тогда 

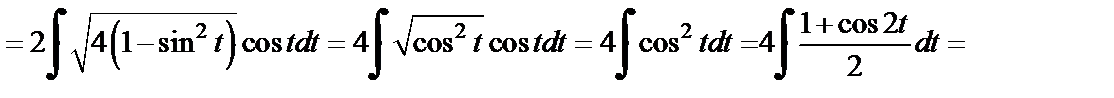

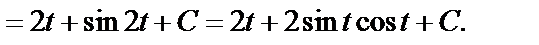
Для вычисления последних интегралов использовали формулы таблицы интегралов. Выразим переменную t через переменную x.
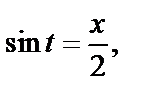
 Тогда
Тогда 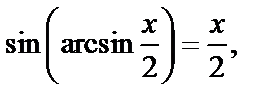

Получаем ответ: 
2) Применим подстановку 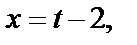 тогда
тогда 
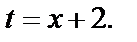 Таким образом,
Таким образом,



Для вычисления интеграла использовали формулу таблицы интегралов.
3) Применим подстановку 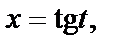 тогда
тогда 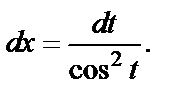 Получаем:
Получаем:
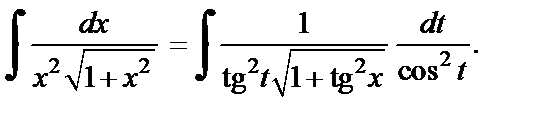
Используя тригонометрическое тождество 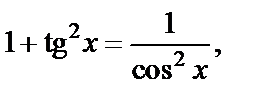 имеем:
имеем:
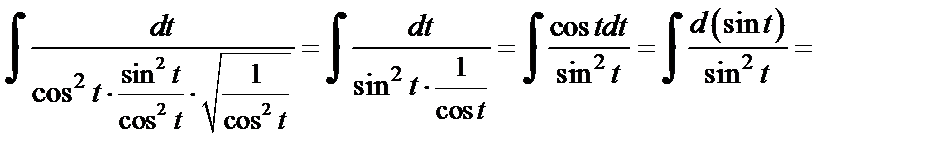

Вернемся к переменной x, для чего выразим t через x из подстановки 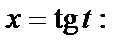
 Тогда
Тогда
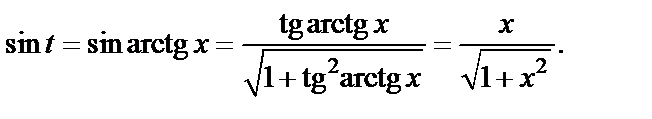 Таким образом,
Таким образом,
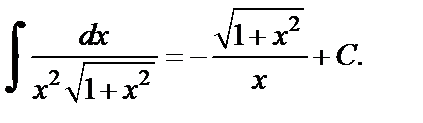
Метод интегрирования по частям
Пусть функции  и
и 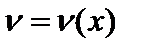 имеют непрерывные производные
имеют непрерывные производные  и
и  Тогда имеет место равенство
Тогда имеет место равенство
 (1)
(1)
Формула (1) задает метод интегрирования по частям, согласно которому интегрирование выражения udv сводится к интегрированию выражения vdu Применение формулы (1) предполагает, что в правой части интеграл 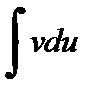 может быть вычислен легче, чем исходный. Формула (19.20) может быть записана также в виде
может быть вычислен легче, чем исходный. Формула (19.20) может быть записана также в виде

Рациональность вычисления некоторых интегралов зависит от того, как выбраны функции  и
и 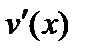 в заданном интеграле.
в заданном интеграле.
Формула интегрирования по частям может применяться неоднократно.
Рассмотрим следующие случаи:
1. Для вычисления интегралов вида 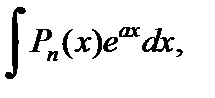
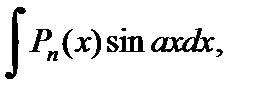
 где
где  – многочлен степени n, в качестве функции
– многочлен степени n, в качестве функции  следует взять многочлен
следует взять многочлен 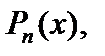 а в качестве
а в качестве  – одно из выражений
– одно из выражений 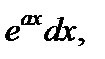

 соответственно. При этом формулу интегрирования по частям следует применять n раз.
соответственно. При этом формулу интегрирования по частям следует применять n раз.
2. Для интегралов вида  и
и 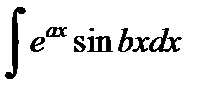 в качестве функции
в качестве функции  можно взять
можно взять 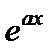 или
или 
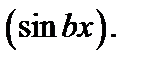 Формулу интегрирования по частям следует применить дважды, а затем из полученного равенства, как из уравнения, найти заданный интеграл.
Формулу интегрирования по частям следует применить дважды, а затем из полученного равенства, как из уравнения, найти заданный интеграл.
3. Для интегралов вида 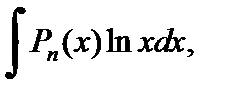


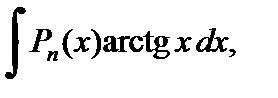


 в качестве u (x) берут функции ln x,
в качестве u (x) берут функции ln x, 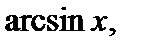
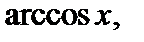

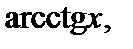

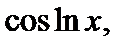 а в качестве dv – выражение
а в качестве dv – выражение 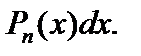 Такой подход используют и тогда, когда
Такой подход используют и тогда, когда 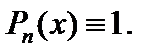
Во многих случаях подынтегральная функция зависит не только от аргумента, но и от натурального индекса n. Методом интегрирования по частям удается привести интеграл к интегралу такой же формы, но с меньшим значением индекса. После нескольких таких шагов приходят к интегралу, который можно вычислить с помощью таблицы. Такой метод интегрирования называют рекуррентным методом, а полученную формулу – рекуррентной формулой.
Пример 1. Методом интегрирования по частям найти неопределенный интеграл:
1) 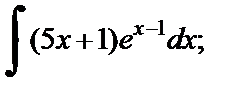 2)
2)  3)
3) 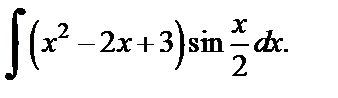
Решение. 1) Положим 
 Тогда
Тогда 
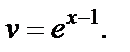 Используя формулу (19.20) интегрирования по частям, получаем:
Используя формулу (19.20) интегрирования по частям, получаем:
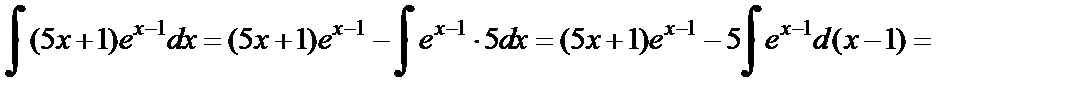

2) Применим формулу (1) интегрирования по частям:
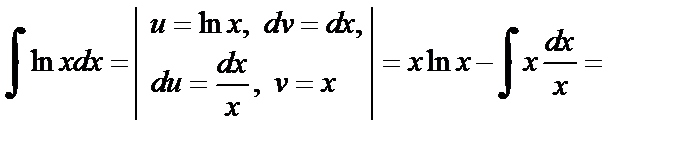
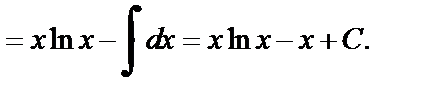
3) Положим 
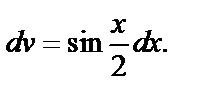 Тогда
Тогда 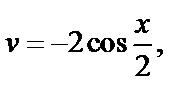
 Применяя формулу (19.20), получаем:
Применяя формулу (19.20), получаем:
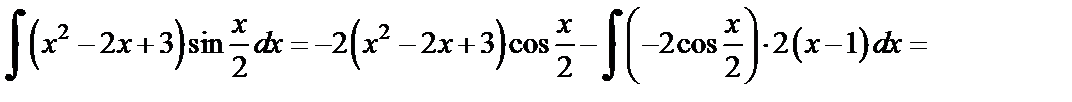

Применив формулу интегрирования по частям, понизили степень многочлена на единицу. Чтобы найти  применим еще раз метод интегрирования по частям. Положим
применим еще раз метод интегрирования по частям. Положим 
 Тогда
Тогда 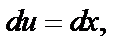
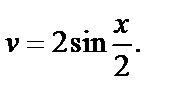 Получаем:
Получаем:



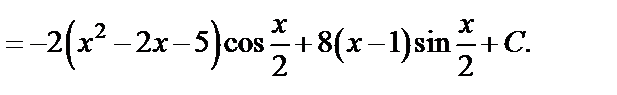
Пример 2. Методом интегрирования по частям найти неопределенный интеграл:
1)  2)
2) 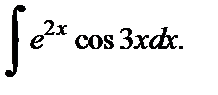
Решение. 1)Интеграл 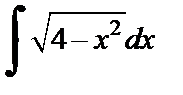 уже был вычислен в параграфе 19.2. (см. пример 2, с. 15–16 данного пособия) методом подстановки. Рассмотрим второй способ его вычисления, используя метод интегрирования по частям:
уже был вычислен в параграфе 19.2. (см. пример 2, с. 15–16 данного пособия) методом подстановки. Рассмотрим второй способ его вычисления, используя метод интегрирования по частям:
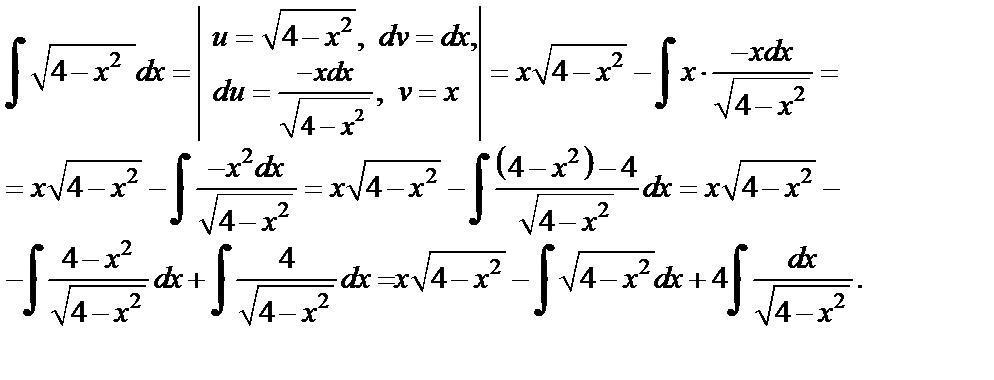
Вычислим последний интеграл, используя формулу (19.14) таблицы интегралов. Получим равенство
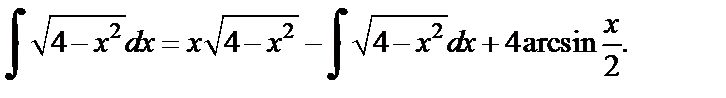
В правой части этого равенства получили исходный интеграл. Найдем его из уравнения:  откуда получаем ответ:
откуда получаем ответ: 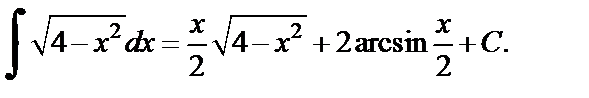
2) Используя формулу интегрирования по частям дважды, получаем:
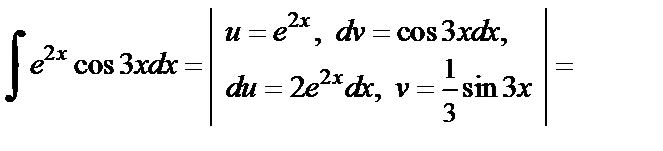

В результате получили равенство

из которого находим:


Приходим к ответу:
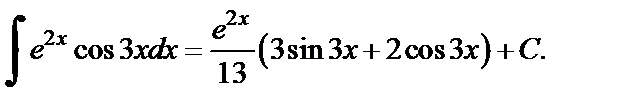
Пример 3. Найти неопределенный интеграл 
Решение. Используя формулу (1) интегрирования по частям, получаем:
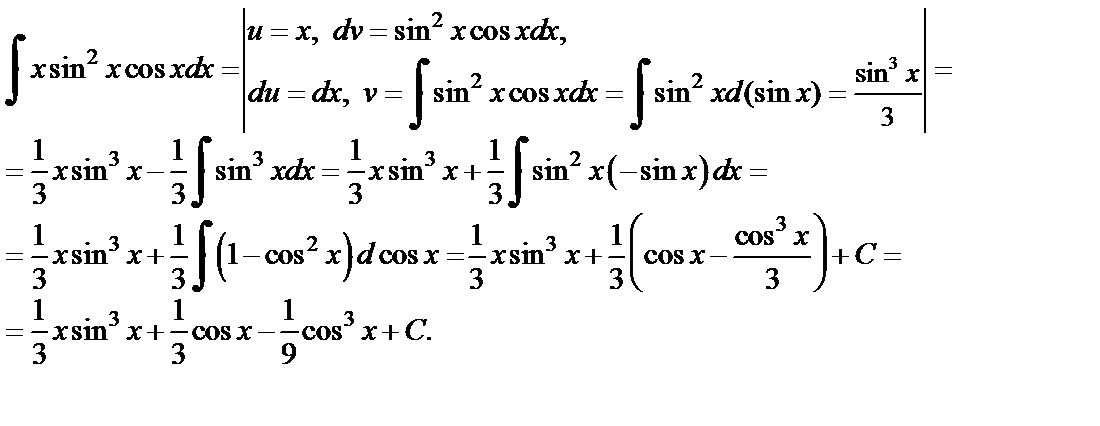
Пример 4. Найти неопределенный интеграл 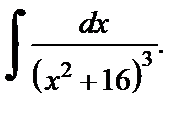
Решение. Преобразуем подынтегральное выражение:

Последний интеграл вычислим, применяя формулу интегрирования по частям.
Полагаем 
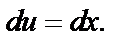
Если  то
то
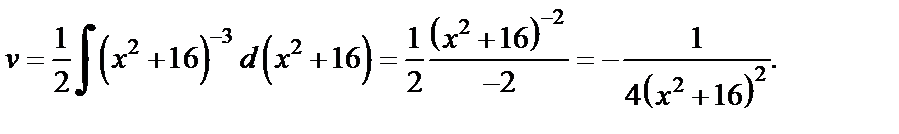
Тогда
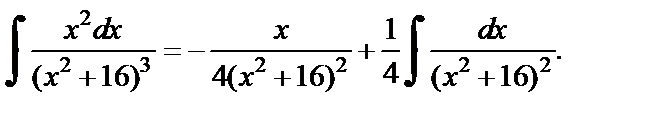
Таким образом, получаем выражение интеграла 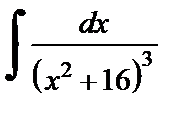 через интеграл
через интеграл 
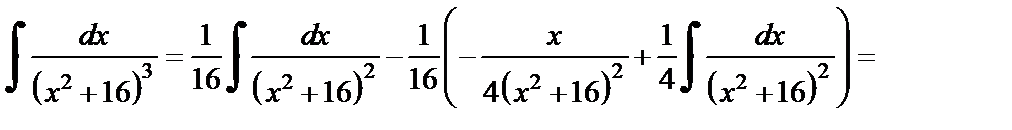

Вычисляем  аналогично первоначальному.
аналогично первоначальному.
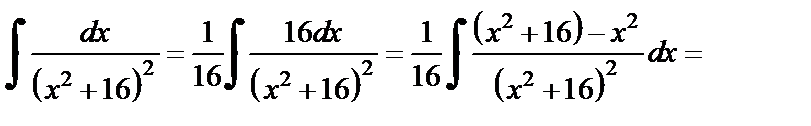

Для вычисления последнего интеграла применяем формулу интегрирования по частям:


Имеем:

Получаем:

Пример 5. Получить рекуррентную формулу для вычисления интеграла  Используя ее, вычислить
Используя ее, вычислить 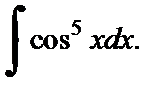
Решение. Обозначим 

Мы получили:

Выражаем:

Это и есть рекуррентная формула, которая позволяет уменьшать показатель степени в подынтегральной функции до тех пор, пока не придем к интегралу  или
или  в зависимости от того, является ли n числом четным или нечетным.
в зависимости от того, является ли n числом четным или нечетным.
Используем ее для вычисления 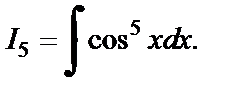



КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Какие методы вычисления неопределенных интегралов вы знаете?
2. В чем заключается метод замены переменной в неопределенном интеграле?
3. Запишите формулу для вычисления неопределенного интеграла по частям.
Домашнее задание: [1], ч.4, §19.2, №1.1, №1.2, §19.4