По имеющимся в следующей таблице данным по группе из 20 студентов заочного отделения необходимо:
а) построить интервальный ряд распределения признака и его график; б) рассчитать модальное, медианное и среднее значение, установить его
типичность с помощью коэффициентов вариации; в) Определение показателей вариации
По данным задания 1 (Корреляционный анализ) выделить три группы по результативному признаку и вычислить:
1. групповую дисперсию;
2. среднюю из групповых;
3. межгрупповую дисперсию;
4. общую дисперсию;
5. среднее квадратическое отклонение;
6. показатель вариации;
7. эмпирический коэффициент детерминации;
8. эмпирическое корреляционное отношение.
Полученные результаты расчетов проанализировать и сделать выводы. Примечание: Общую дисперсию определить по правилу сложения дисперсий и проверить обычным способом.
Типовая задача. Имеются следующие данные о возрастном составе студентовгруппы заочного отделения ВУЗа (лет): 19; 19; 19; 20; 20; 20; 20; 20; 20; 20; 20;
20; 21; 21; 21; 22; 23; 23; 24; 25; 25; 25; 26; 27; 29.
Для анализа распределения студентов по возрасту требуется: 1) построить интервальный ряд распределения и его график; 2) рассчитать модальный, медианный и средний возраст, установить его типичность с помощью коэффициентов вариации; 3) проверить распределение на нормальность с помощью коэффициентов асимметрии и эксцесса.
Решение. Для построения интервального ряда из дискретногоиспользуется формула Стерджесса, с помощью которой определяется оптимальное количество интервалов (n):
| n = 1 +3,322 lg N, | (12) |
где N – число величин в дискретном ряде.
В нашей задаче n = 1 + 3,322 lg 25 = 1 + 3,322*1,398 = 5,64. Так как число интервалов не может быть дробным, то округлим его до ближайшего целого числа, т.е. до 6.
После определения оптимального количества интервалов определяем размах интервала по формуле:
| h = H / n, | (13) |
где H – размах вариации, определяемый по формуле (14).
| H = Хмах –Хmin, | (14) |
где Xмax и Xmin — максимальное и минимальное значения в совокупности.
В нашей задаче h = (29 – 19)/6 = 1,67.
Интервальная группировка данных приведена в первом столбце таблицы Ошибка! Источник ссылки не найден. 3,которая содержит также алгоритм ипромежуточные расчеты.
Таблица13
Вспомогательные расчеты для решения задачи
| Xi, лет | fi | Xi | Xi*fi | Xi-X | (Xi-Х)fi | (Xi-X)2 | (Xi-X)2fi | (Xi-X)3fi | (Xi-X)4fi |
| до 20,67 | 19,833 | 237,996 | -2,134 | 25,602 | 4,552 | 54,623 | -116,539 | 248,638 | |
| 20,67-22,33 | 21,5 | 86,000 | -0,467 | 1,866 | 0,218 | 0,871 | -0,406 | 0,189 | |
| 22,33-24 | 23,167 | 69,501 | 1,200 | 3,601 | 1,441 | 4,323 | 5,190 | 6,231 | |
| 24-25,67 | 24,833 | 74,499 | 2,866 | 8,599 | 8,217 | 24,650 | 70,659 | 202,543 | |
| 25,67-27,33 | 26,5 | 53,000 | 4,533 | 9,067 | 20,552 | 41,105 | 186,348 | 844,806 | |
| Более 27,33 | 28,167 | 28,167 | 6,200 | 6,200 | 38,446 | 38,446 | 238,383 | 1478,091 | |
| Итого | - | 549,163 | - | 54,937 | - | 164,018 | 383,636 | 2780,498 |
На основе этой группировки строится график распределения возраста студентов.
Мода (M 0)– это наиболее часто повторяющееся значение признака. Для интервального ряда с равными интервалами величина моды определяется по формуле (13):
Формула для вычисления:
| M 0 | = X M | + iM | fM | - fM | 0 -1 | , | (15) | |||||||
| (fM 0 | - fM 0-1 | )+(fM 0- fM 0+1) | ||||||||||||
| где X M | – нижняя граница модального интервала; iM | – величина модального | ||||||||||||
| e |
интервала; fM 0, fM 0 -1, fM 0 +1 – частоты в модальном, предыдущем и следующем за
модальным интервалом соответственно.
Модальный интервал определяется по наибольшей частоте.
В нашей задаче чаще всего повторяется (12 раз) первый интервал возраста (до 20,67), значит, это и есть модальный интервал. Используя формулу (13), определяем точное значение модального возраста:
Мо=19+1,667*(12-0)/(2*12-4-0)=20 (лет).
Медиана М е – варианта, которая находится в середине вариационного ряда, которая делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значением признака больше медианы.
Вычисляется медиана по формуле:
| S f | - SM | ||||||
| М е = Х М | + iM | × | e -1 | (16) | |||
| е | |||||||
| e | fM | ||||||
| e |
где Х М е – нижняя граница медианного интервала;
iM e –медианный интервал;
å f – половина от общего числа наблюдений;
SM e -1–сумма наблюдений,накопленная до начала медианного интервала;
fMe –число наблюдений или объем взвешивающего признака в медианноминтервале.
В нашей задаче второй интервал возраста (от 20,67 до 22,33) является медианным, так как на него приходится середина ряда распределения возраста. Определяем точное значение медианного возраста:
Ме = 20,67 + 1,667*(12,5-12)/4 = 20,878 (года).
Средняя величина –это обобщающий показатель совокупности,характеризующий уровень изучаемого явления или процесса. Средние величины могут быть простыми(17) и взвешенными (18).
| = m å X i m | ; | (17) | å X i mf i . | (18) | ||||||
| X | X = m | |||||||||
| N | å f i |
При этом обозначено: Xi – значения отдельных статистических величин или середин группировочных интервалов; m - показатель степени, от значения которого зависят виды средних величин. Выбор вида формулы средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять. Показатель степени m в общей формуле средней величины оказывает существенное влияние на значение средней величины: по мере увеличения степени возрастает и средняя величина (правило
| мажорантности средних величин), то есть X ГМ | < X геом < Х ар | < Х КВ < Х куб. Так, | |||||||||||||||
| если m ® +¥, то X ® X max, а если m ® -¥, то X ® X min . | |||||||||||||||||
| В нашей задаче, применяя формулу | средней | арифметической | |||||||||||||||
| взвешенной и подставляя вместо Х i | середины интервалов возраста ХИ, | ||||||||||||||||
| определяем средний возраст студентов: | Х ар = 549,163/25 = 21,967 (года).Теперь |
осталось определить типичность или нетипичность найденной средней величины. Это осуществляется с помощью расчета показателей вариации. Чем ближе они к нулю, тем типичнее найденная средняя величина для изучаемой статистической совокупности.
Дисперсия – это средний квадрат отклонений индивидуальных значений от средней арифметической (не имеет единиц измерения).
дисперсия:
| å(x - | )2 | ||||||||||||
| s | = | x | —для несгруппированных данных; | (18) | |||||||||
| n | s | ||||||||||||
| å(x - | )2 f | ||||||||||||
| s | x | — для сгруппированных данных; | (19) | ||||||||||
| = | å f | ||||||||||||
| среднее квадратическое отклонение s = s 2. | (20) | ||||||||||||
Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю представляемую совокупность.
коэффициент вариации:
| n = | s | ×100%, | (21) | |
| X |
По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. При этом критериальным значением коэффициента вариации служит 1/3.
Чем больше его величина, тем больше разброс значений признаков вокруг средней величины, тем менее однородна совокупность по своему составу и тем менее представительна средняя величина.
Если совокупность разбита на группы по изучамому признаку, то для такой совокупности могут быть вычислены следующие виды дисперсии:
a) групповые (частные):
| d | = | å(x - | —для несгруппированных данных; | (22) | ||||||||||
| n | ||||||||||||||
| d | = | å(x - | f | — для сгруппированных данных; | (23) | |||||||||
| å f | ||||||||||||||
| å si 2 f | ||||||||||||||
| б) средняя из групповых | s | = | ; | (24) | ||||||||||
| i | å f | |||||||||||||
| в) межгрупповая | d | = | å(x - | ; | (25) | |||||||||
| å f | ||||||||||||||
| г) Общая дисперсия по | закону сложения дисперсий равна сумме |
средней из групповых дисперсий и межгрупповой дисперсии.
| s | = s | + d | |||||
| i | , | (26) | |||||
Это соотношение называют правилом сложения дисперсий.
| Эмпирический коэффициент детерминации (h | ) - показатель, | ||
представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
| d | 2 | ||||||
| h | = | , | (24) | ||||
| s | |||||||
где d 2 - величина межгрупповой дисперсии,
s 2 - величина общей дисперсии.
При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи- единице.
Эмпирическое корреляционное отношение – есть корень квадратный из отношения межгрупповой дисперсии к общей:
| d | 2 | ||||||
| h | = | ||||||
| Э | s | ||||||
| , | (27) | ||||||
| Эмпирическое корреляционное отношение характеризует влияние | |||||||
| группировочного признака на результативный признак | (оба показателя |
(числитель и знаменатель) не превышают по своей величине единицы: чем больше показатели в этих пределах, тем теснее взаимосвязь между изучаемыми признаками).
hЭ ® max при d 2 = s 2 (si 2); hЭ – влияние других факторов равно 0.
hЭ ® min при d 2 = 0(h min = 0) – влияние признака равно 0.
Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока:
| h | 0,1-0,3 | 0,3-0,5 | 0,5-0,7 | 0,7-0,9 | 0,9-0,99 |
| сила связи | слабая | умеренная | заметная | тесная | весьма тесная |
Тема 3. Ряды динамики
| Типовая задача. Объем СМР | с 2002-2011гг. характеризуется следующим рядом | |||||||||||
| динамики. | ||||||||||||
| Год | ||||||||||||
| Объем | ||||||||||||
| СМР,тыс. | 1163,5 | 1113,7 | 1100,3 | 1094,1 | 1187,8 | 1231,4 | 1253,1 | 1308,1 | 1330,5 | 1287,7 | ||
| руб.. |
Вычислить: абсолютные, относительные, средние изменения и их темпы базисным и цепным способами. Проверить ряд на наличие в нем линейного тренда, на основе которого рассчитать интервальный прогноз на 2012 год с вероятностью
95%.
Решение. Любое изменение уровней ряда динамики определяется базисным (сравнение с первым уровнем) и цепным (сравнение с предыдущим уровнем) способами. Оно может быть абсолютным (разность уровней ряда) и относительным (соотношение уровней).
Базисное абсолютное изменение представляет собой разность конкретного ипервого уровней ряда (36), а цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда (47).
| D Y Б = Y - Y. | (36) | D Y Ц = Y - Y | . | (47) |
| i 1 | ii -1 |
По знаку абсолютного изменения делается вывод о характере развития явления: при D Y > 0 — рост, при D Y < 0 — спад, при D Y = 0 — стабильность.
В нашей задаче эти изменения определены в 3-м и 4-м столбцах таблицы 1. Для проверки правильности расчетов применяется правило, согласно которому сумма цепных абсолютных изменений равняется последнему базисному. В нашей задаче это правило выполняется: åD Y Ц = 124,2 и D Y 2004 Б = 124,2.
Базисное относительное изменение представляет собой соотношениеконкретного и первого уровней ряда (28), а цепное относительное изменение представляет собой соотношение конкретного и предыдущего уровней ряда (29).
| i Б = Yi Y. | (28) | i Ц = Yi Y | . | (29) |
| i -1 |
Относительные изменения уровней — это по существу индексы динамики, критериальным значением которых служит 1. Если они больше ее, имеет место рост явления, меньше ее — спад, а при равенстве единице наблюдается стабильность явления.
В нашей задаче эти изменения определены в 5-м и 6-м столбцах таблицы 1. Вычитая единицу из относительных изменений, получают темп изменения
уровней, критериальным значением которого служит 0. При положительном темпе изменения имеет место рост явления, при отрицательном — спад, а при нулевом темпе изменения наблюдается стабильность явления. В нашей задаче темпы изменения определены в 7-м и 9-м столбцах таблицы 1, а в 8-м и 10-м сделан вывод о
характере развития изучаемого явления. Для проверки правильности расчетов применяется правило, согласно которому произведение цепных относительных изменений равняется последнему базисному. В нашей задаче это правило выполняется: Õ i Ц =1,107 и i 2004 Б =1,107.
Таблица 1. Вспомогательные расчеты для решения задачи
| Год | Y | D Y Б | D Y Ц | i Б | i Ц | TБ | хар-р | ТЦ | хар-р | |||||||
| 1163,5 | ||||||||||||||||
| 1113,7 | -49,8 | -49,8 | 0,96 | 0,96 | -0,04 | спад | -0,04 | спад | ||||||||
| 1100,3 | -63,2 | -13,4 | 0,95 | 0,99 | -0,05 | спад | -0,01 | спад | ||||||||
| 1094,1 | -69,4 | -6,2 | 0,94 | 0,99 | -0,06 | спад | -0,01 | спад | ||||||||
| 1187,8 | 24,3 | 93,7 | 1,02 | 1,09 | 0,021 | рост | 0,086 | рост | ||||||||
| 1231,4 | 67,9 | 43,6 | 1,06 | 1,04 | 0,058 | рост | 0,037 | рост | ||||||||
| 1253,1 | 89,6 | 21,7 | 1,08 | 1,02 | 0,077 | рост | 0,018 | рост | ||||||||
| 1308,1 | 1,12 | 1,04 | 0,124 | рост | 0,044 | рост | ||||||||||
| 1330,5 | 22,4 | 1,14 | 1,02 | 0,144 | рост | 0,017 | рост | |||||||||
| 1287,7 | -42,8 | 1,11 | 0,97 | 0,107 | рост | -0,03 | спад | |||||||||
| Итого | 1,11 | |||||||||||||||
Обобщенной характеристикой ряда динамики является средний уровень ряда y. Способ расчета y зависит от того, моментный ряд или интервальный.
В нашей задаче ряд динамики интервальный, значит, применяем формулу средней арифметической простой: y = 12070,2 / 10 = 1207,02 (тыс. руб.). То есть за период 2002-2011г. в строительной организации в среднем объем строительно-монтажных работ увеличился на 1207,02 тыс. руб.
Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.
Базисное среднее абсолютное изменение –это частное от деления последнегобазисного абсолютного изменения на количество изменений уровней (50). Цепное среднее абсолютное изменение уровней ряда–это частное от деления суммы всехцепных абсолютных изменений на количество изменений (61).
| Б | = | D YnБ | (50) | Ц | = | åD Y Ц | (61) | |||||
| D Y | . | D Y | . | |||||||||
| n -1 | n -1 |
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность. Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными. В нашей задаче D Y = 124,2/9 = 13,8.
Наряду со средним абсолютным изменением рассчитывается и среднее относительное. Базисное среднее относительное изменение определяется по формуле (72), а цепное среднее относительное изменение – по формуле (83):
| = n -1 Yn | ||||||||
| i Б= n -1 | inБ | . | (72) | i Ц= n -1Õ iпЦ. | (83) | ||||
| Y 1 |
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность. В нашей задаче i =9 
1,107 = 1,0114, то есть ежегодно объем строительно-монтажных работ
увеличивается в 1,0114 раза.
Вычитанием 1 из среднего относительного изменения образуется соответствующий средний темп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики. В нашей задаче T = 1,0114 – 1 = 0,0114, то есть ежегодно объем строительно-монтажных работ растет на 1,14%. (0,0114*100%=1.14%)
Проверка ряда динамики на наличие в нем тренда (тенденции развития ряда) возможна несколькими способами (метод средних, Фостера и Стюарта, Валлиса и Мура и пр.), но наиболее простым является графическая модель, где на графике по оси абсцисс откладывается время, а по оси ординат – уровни ряда. Соединив полученные точки линиями, в большинстве случаев можно выявить тренд визуально. Тренд может представлять собой прямую линию, параболу, гиперболу и т.п. В итоге приходим к трендовой модели вида:
| Yt | ˆ | + et, | (94) | ||
| = yt | |||||
| где | ˆ | развития; | et – случайное или циклическое | ||
| yt –математическая функция |
отклонение от функции; t – время в виде номера периода (уровня ряда). Цель такого
| ˆ | ||||||||||||||
| метода – выбор теоретической зависимости yt в качестве одной из функций: | ||||||||||||||
| ˆ | = a0 + a1t –прямая линия; | ˆ | = a0 | + | a1 | ˆ | = a0 + a1t + a2t | 2 | – | парабола; | ||||
| yt | yt | t | – гипербола; yt | |||||||||||
| a1 | – степенная; | m | – ряд Фурье. | |||||||||||
| y ˆ t = a0t | ˆ | = a0 | + å(ak cos kt + bk sin kt) | |||||||||||
| yt | ||||||||||||||
| k = 1 |
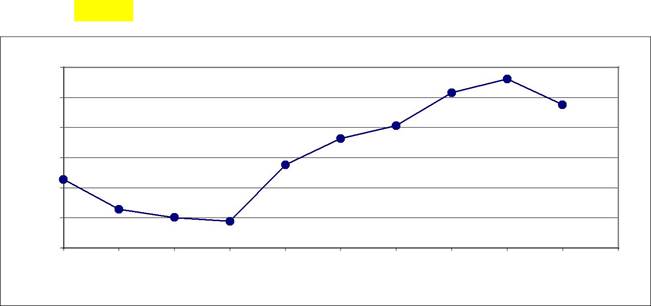
Для выявления тренда (тенденции развития ряда) в нашей задаче построим график Y(t) (рис.4):
| 1330,5 | |||||||||||
| 1308,1 | |||||||||||
| 1287,7 | |||||||||||
| 1253,1 | |||||||||||
| 1231,4 | |||||||||||
| 1187,8 | |||||||||||
| 1163,5 | |||||||||||
| 1113,7 | 1100,3 | ||||||||||
| 1094,1 | |||||||||||
Рис.. График динамики объема строительно-монтажных работ с 2002 -2012гг.
Из данного графика видно, что есть все основания принять уравнение тренда в виде линейной функции.
Определение параметров an в этих функциях может вестись несколькими
способами, но самые незначительные отклонения аналитических (теоретических) уровней (y ˆ t – читается как «игрек, выравненный по t ») от фактических (Yt) дает
метод наименьших квадратов – МНК. При этом методе учитываются всеэмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней Yt от теоретических уровней y ˆ t:
| å(y ˆ t - y) 2 ® min. | (10) | |||
| В нашей задаче при выравнивании по прямой вида | ˆ | = a0 + a1t | параметры a0 и a1 | |
| yt |
отыскиваются по МНК следующим образом. В формуле (94) вместо y ˆ t записываем его конкретное выражение a0 + a1t. Тогда S = å(a 0 + a 1 t - y)2 ® min. Дальнейшее
решение сводится к задаче на экстремум, т.е. к определению того, при каком значении a0 и a1 функция двух переменных S может достигнуть минимума. Как
известно, для этого надо найти частные производные S по a0 и a1, приравнять их к
нулю и после элементарных преобразований решить систему двух уравнений с двумя неизвестными.
В соответствии с вышеизложенным найдем частные производные:
| ì | ¶ S | = 2 | å(a 0 | + a 1 t - y)=0 | |
| ï | ¶ a 0 | ||||
| ï | |||||
| í | ¶ S | ||||
Поиск по сайту©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование. Дата создания страницы: 2016-04-27 Нарушение авторских прав и Нарушение персональных данных |
Поиск по сайту: Читайте также: Деталирование сборочного чертежа Когда производственнику особенно важно наличие гибких производственных мощностей? Собственные движения и пространственные скорости звезд |