Раздаточный материал
Приближенная оценка нормальности распределения исследуемой величины может быть выполнена с использованием выборочных характеристик: коэффициента асимметрии и эксцесса, определяемых по формулам
k
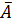 = Sni (xi - = Sni (xi - 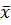 )3 / (n.Sx3),
i=1 )3 / (n.Sx3),
i=1
| (31) | |
k
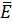 = Sni (xi - = Sni (xi - 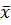 )4 / (n.Sx4),
i=1 )4 / (n.Sx4),
i=1
| (32) |
где  - эмпирический коэффициент асимметрии;
- эмпирический коэффициент асимметрии;
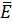 - эксцесс.
- эксцесс.
Пример. По данным, приведенным в табл.8, вычислить эмпирический коэффициент асимметрии и эксцесс для распределения давлений в гидросистеме управления дорожной машины.
12.3689
Коэффициент асимметрии 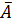 = - ------------ = -0.47.
= - ------------ = -0.47.
46.407 120.0.603
Эксцесс 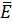 = ------------ -3 = -0.03.
= ------------ -3 = -0.03.
120.0.604
Вспомогательные вычисления заносим в табл.12.
Таблица 12
Расчет эмпирических характеристик асимметрии и эксцесса распределения давлений в гидросистеме управления дорожной машины
| № интервала | Эмпирическая частота | Середина интервалов |
(Rj -  )3.nj )3.nj
|
(Rj -  )4.nj )4.nj
|
| j | nj | Rj, | ||
| 3.96 | -15.8826 | 23.3474 | ||
| 4.36 | -6.1252 | 6.5540 | ||
| 4.86 | -4.2107 | 2.8212 | ||
| 5.16 | -0.5118 | 0.1382 | ||
| 5.56 | 0.0659 | 0.0086 | ||
| 5.96 | 4.7641 | 2.5250 | ||
| 6.36 | 4.8261 | 4.4883 | ||
| 6.76 | 4.7053 | 6.2580 | ||
| -12.3689 | 46.1407 | |||
Более строгий метод проверки гипотезы о нормальном распределении результатов экспериментальных исследований основан на использовании «хи-квадрат» критерия, разработанного К.Пирсоном. Сущность этого метода заключается в оценке меры
P(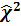 > c 2a,k-r-1) = a, > c 2a,k-r-1) = a,
| (33) |
где 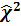 - вычисленное значение «хи-квадрат» критерия:
- вычисленное значение «хи-квадрат» критерия:
k (nj - njT)2
 =S ------------;
i=1 njT =S ------------;
i=1 njT
| (34) |
nj - эмпирическая частота;
njT - теоретическая частота попадания наблюдений в j-й интервал,
| njт = n . Pj; | (35) |
n - объем наблюдений;
Pj - теоретическая вероятность, численно равная площади, ограниченной сверху кривой распределения Гаусса, а снизу - верхней и нижней границами j-го интервала,
| Pj = P(xjн < x < xjв) = P(z1 < z < z2) = Ф(z2) - Ф(z1), | (36) |
где xjн и xjв - соответственно нижняя и верхняя границы j-го интервала;
z1 и z2 - нормированные случайные величины
xjн - 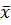 z1 = --------
Sx
z1 = --------
Sx
| ü ÷ ÷ ÷ | ||
xjв - 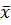 z2 = -------
Sx
z2 = -------
Sx
| ý ÷ ÷ þ | ; (37) |
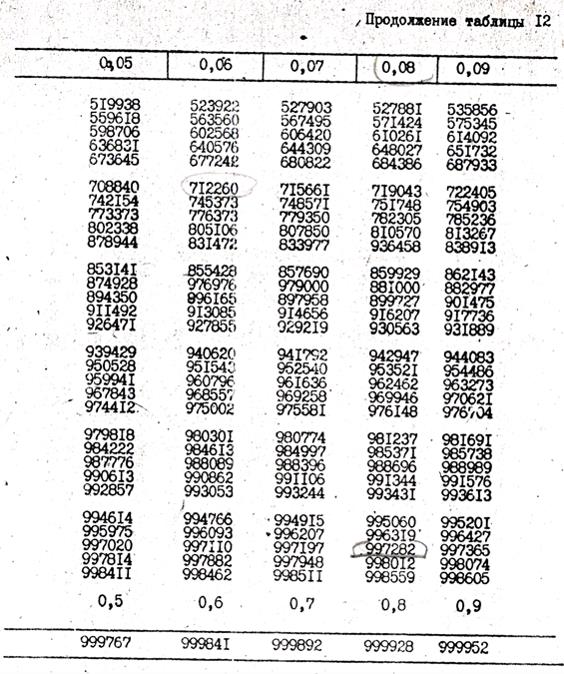
Ф(z2) и Ф(z1) - интегралы вероятностей /2/:
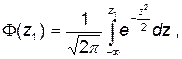
| (38) | |
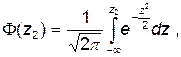
| (39) |
c 2 a ,k-r-1 - критическое значение «хи-квадрат» критерия, взятое по табл.13 при уровне значимости a и числе степеней свободы
| f = k - r - 1, | (40) | |
где r - число выборочных оценок, использованное для расчета теоретических частот njT, равное двум.
k – число интервалов
| При | ì÷ í | 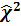 >c2a,f >c2a,f
| гипотеза отвергается (имеют место большие отклонения наблюдаемых частот от теоретических); |
| ÷ î |
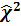 <c2a,f <c2a,f
| гипотеза принимается. |
Таблица 13
Значения c 2 a ,f по данным /5/
| Число степеней | Уровень значимости a | ||
| свободы f | 0.05 | 0.025 | 0.01 |
| 3.8 | 5.0 | 6.6 | |
| 6.0 | 7.4 | 9.2 | |
| 7.8 | 9.4 | 11.3 | |
| 9.5 | 11.1 | 13.3 | |
| 11.1 | 12.8 | 15.1 | |
| 12.6 | 14.4 | 16.8 | |
| 14.1 | 16.0 | 18.5 | |
| 15.5 | 17.5 | 20.1 | |
| 16.9 | 19.0 | 21.7 | |
| 18.3 | 20.5 | 23.2 |
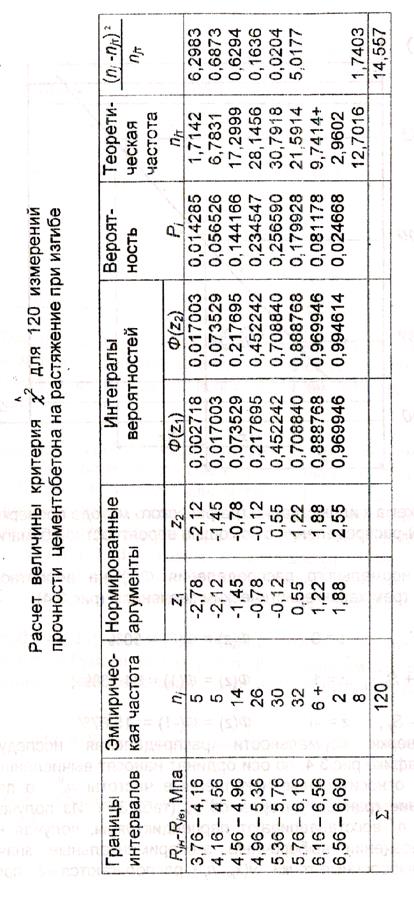
Пример. По данным примера проверить статистическую гипотезу о нормальном распределении давлений в гидросистеме управления с использованием критерия согласия c 2 К.Пирсона.
Решение. Для расчета критерия 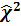 используем зависимость (34). Последовательность расчета показана в табл.14, графы 1 и 2 табл.14 заполнены по данным табл.8. Частоты nj, меньшие 5, объединены согласно условиям применения c 2 - критерия.
используем зависимость (34). Последовательность расчета показана в табл.14, графы 1 и 2 табл.14 заполнены по данным табл.8. Частоты nj, меньшие 5, объединены согласно условиям применения c 2 - критерия.
При числе степеней свободы f=k-r-1=8-2-1=5 и уровне значимости a =0.05 по табл. 3.13 находим критическое значение «хи-квадрат»
критерия c 20.05;5=11,1. Поскольку имеет место неравенство 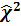 =14.56 > c 2 0.05; 5 = 11,1, то исходная гипотеза должна быть отвергнута.
=14.56 > c 2 0.05; 5 = 11,1, то исходная гипотеза должна быть отвергнута.
Графический метод проверки гипотезы выполняют с помощью вероятностной бумаги, на которой в прямоугольной системе координат на оси ординат нанесена шкала, соответствующая интегралу Гаусса
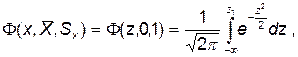
| (41) |
а по оси абсцисс - линейная или логарифмическая шкала
аргумента х.
Функцию нормального распределения Ф(z) на вероятностной сетке строят по трем характеристическим значениям (рис.4):
| при |
x = 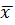 , ,
| z = 0 | Ф(z) = Ф(0) = 50%; |
x = 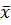 + Sx , + Sx ,
| z = 1 | Ф(z) = Ф(1) = 84.13%; | |
x = 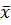 - Sx , - Sx ,
| z = -1 | Ф(z) = Ф(-1) = 15.87%. |

Рис.4. Схема к иллюстрации графического метода проверки гипотезы N-распределения с помощью вероятностной бумаги
Таблица 14
Графическая интерпретация результатов исследований
И нтерпретацию результатов экспериментальных исследований в виде гистограммы, полигона частот и функции распределения исследуемой величины.
Гистограммой называют ступенчатую функцию, построенную в системе координат D j , nj (или D j , njI ).
Полигон частот или многоугольник распределения (эмпирическую кривую распределения) строят также в прямоугольных координатах, откладывая по оси абсцисс середины интервалов хj (табл.8), а по оси ординат - абсолютные (или относительные) частоты nj.
Эмпирической функцией распределения называется
функция  (x), определяющая для каждого значения исследуемой величины x ее относительную частоту.
(x), определяющая для каждого значения исследуемой величины x ее относительную частоту.
Функция  (x) обладает следующими свойствами:
(x) обладает следующими свойствами:
1)  (x) - неубывающая функция;
(x) - неубывающая функция;
2) значения эмпирической функции распределения  (x) принадлежат отрезку (0,1);
(x) принадлежат отрезку (0,1);
3) при x < xmin  (x)=0; при x > xmax
(x)=0; при x > xmax  (x)=1.
(x)=1.
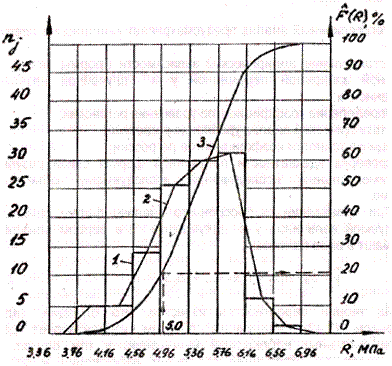
Рис.5. Графическая интерпретация результатов исследования изменения давления в гидросистеме управления дорожной машины:
1 - гистограмма; 2 - полигон частот; 3 – эмпирическая функция распределения
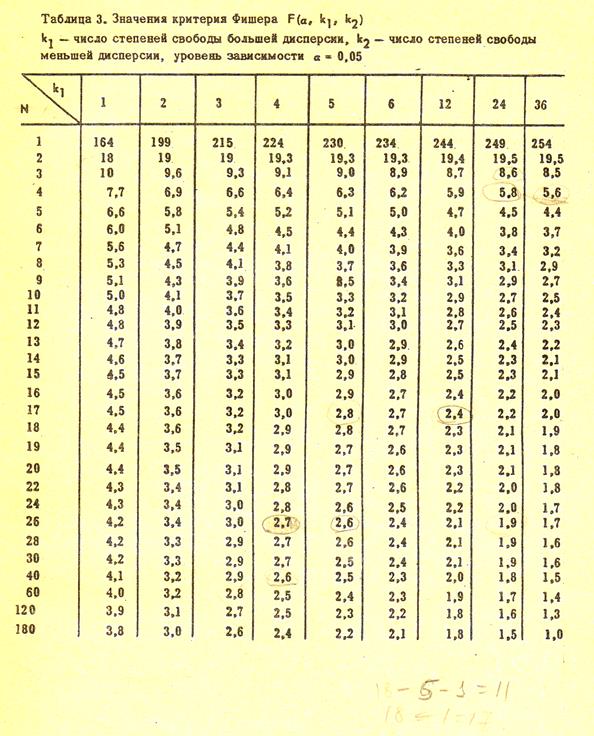
Значения критерия Фишера