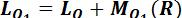 . (1.62)
. (1.62)
По формуле для векторного момента силы имеем
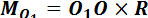 . (1.63)
. (1.63)
С учетом этого (1.62) примет форму
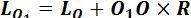 . (1.64)
. (1.64)
1.5.2. Частные случаи приведения пространственной
системы сил
Произвольная система сил приводится к силе, равной главному вектору  , и паре сил, векторный момент которой равен главному моменту
, и паре сил, векторный момент которой равен главному моменту 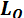 . В зависимости от их модулей и взаимного направления, т. е. угла
. В зависимости от их модулей и взаимного направления, т. е. угла  между ними, можно провести дальнейшие упрощения.
между ними, можно провести дальнейшие упрощения.
1. Приведение к паре сил. Если 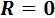 ,
,  , то система сил приводится к одной паре сил, причем главный момент в этом случае, согласно (1.62), не зависит от центра приведения. В рассматриваемом случае оба инварианта системы сил равна нулю, т. е.
, то система сил приводится к одной паре сил, причем главный момент в этом случае, согласно (1.62), не зависит от центра приведения. В рассматриваемом случае оба инварианта системы сил равна нулю, т. е.
 (1.65)
(1.65)
2. Приведение к равнодействующей. Возможны два случая:
· если  (первый инвариант
(первый инвариант 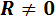 , второй –
, второй –  ), то система приводится к равнодействующей силе
), то система приводится к равнодействующей силе  , равной по модулю и направлению главному вектору
, равной по модулю и направлению главному вектору  , т. е.
, т. е.
 (1.66)
(1.66)
Линия действия равнодействующей силы в этом случае проходит через центр приведения (рис. 1.20);
·  если
если  , но
, но  , то есть
, то есть  , то система сил тоже приводится к равнодействующей, причем опять
, то система сил тоже приводится к равнодействующей, причем опять

Но линия действия равнодействующей силы в этом случае  отстоит от центра приведения на расстоянии
отстоит от центра приведения на расстоянии 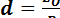 (рис. 1.21). Рис. 1.20
(рис. 1.21). Рис. 1.20
Действительно, в этом случае имеем силу и пару сил с векторным моментом 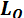 , причем силы пары можно считать расположенными в одной плоскости с силой
, причем силы пары можно считать расположенными в одной плоскости с силой  , так как векторный момент пары перпендикулярен силе
, так как векторный момент пары перпендикулярен силе  (см. рис. 1.21). Поворачивая и перемещая пару сил в ее плоскости, а также изменяя силы пары и ее плечо, при сохранении векторного момента можно получить одну из сил пары
(см. рис. 1.21). Поворачивая и перемещая пару сил в ее плоскости, а также изменяя силы пары и ее плечо, при сохранении векторного момента можно получить одну из сил пары  , равной по модулю, но противоположной по направлению главному вектору
, равной по модулю, но противоположной по направлению главному вектору  Другая сила пары
Другая сила пары  и будет равнодействующей силой. Действительно,
и будет равнодействующей силой. Действительно,
 , (1.67)
, (1.67)
так как система двух равных по модулю, но противоположных по направлению сил  и может быть отброшена. Таким образом, рассматриваемая система сил отказалась эквивалентной одной равнодействующей силе
и может быть отброшена. Таким образом, рассматриваемая система сил отказалась эквивалентной одной равнодействующей силе  , которая по модулю и направлению совпадает с главным вектором
, которая по модулю и направлению совпадает с главным вектором  . Плечо пары сил
. Плечо пары сил  определяется из условия
определяется из условия





Рис.1.21 Рис.1.22 Рис.1.23
так как  . Отрезок
. Отрезок 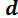 определяет кратчайшее расстояние от центра приведения О до линии действия равнодействующей силы
определяет кратчайшее расстояние от центра приведения О до линии действия равнодействующей силы  .
.
3. Приведение к динаме. Динамой в механике называют такую совокупность силы  и пары сил
и пары сил  ), действующих на твердое тело, у которой сила перпендикулярна плоскости действия пары сил (рис. 1.22). Используя векторный момент
), действующих на твердое тело, у которой сила перпендикулярна плоскости действия пары сил (рис. 1.22). Используя векторный момент  пары сил
пары сил  , можно также определить динаму как совокупность силы и пары, у которых сила параллельна векторному моменту пары сил (рис. 1.23). Сила
, можно также определить динаму как совокупность силы и пары, у которых сила параллельна векторному моменту пары сил (рис. 1.23). Сила  и векторный момент пары сил могут быть направлены как в одну, так и в противоположные стороны. Рассмотрим теперь случай, в котором
и векторный момент пары сил могут быть направлены как в одну, так и в противоположные стороны. Рассмотрим теперь случай, в котором  и векторы
и векторы 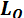 и
и  не перпендикулярны (рис. 1.24). В этом случае оба инварианта не равны нулю, т. е.
не перпендикулярны (рис. 1.24). В этом случае оба инварианта не равны нулю, т. е.
 (1.69)
(1.69)
 Система сил в этом случае приводится к динаме, причем элементами динамы являются сила
Система сил в этом случае приводится к динаме, причем элементами динамы являются сила  и момент пары
и момент пары  , где
, где  – угол между векторами
– угол между векторами 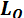 и
и  .
.
Действительно, после приведения системы к центру О получим главный вектор  и
и
Рис.1.24 главный момент 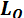 . Косинус угла
. Косинус угла  меду ними можно определить, выражая скалярное произведение векторов
меду ними можно определить, выражая скалярное произведение векторов 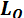 и
и  в двух формах:
в двух формах:


Разложим главный момент 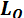 на две взаимно перпендикулярные составляющие
на две взаимно перпендикулярные составляющие  и
и 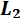 , одна из которых
, одна из которых  направлена по главному вектору
направлена по главному вектору  (рис. 1.24). Имеем
(рис. 1.24). Имеем
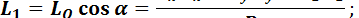

Векторный момент пары сил 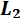 перпендикулярен главному вектору
перпендикулярен главному вектору  и пары с моментом
и пары с моментом 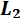 приведется в одной силе
приведется в одной силе  , линия действия которой находится от точки О на расстоянии
, линия действия которой находится от точки О на расстоянии

Рассматриваемая система сил заменилась эквивалентной системой сил, состоящей из силы  и пары сил с векторным моментом
и пары сил с векторным моментом  , который как свободный вектор можно перенести из точки О в любую другую точку, в том числе и точку
, который как свободный вектор можно перенести из точки О в любую другую точку, в том числе и точку  на линии действия силы
на линии действия силы  . Кратко результат можно выразить в форме
. Кратко результат можно выразить в форме
 . (1.73)
. (1.73)
Причем система сил 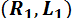 является динамой. Сила
является динамой. Сила  и векторный момент пары
и векторный момент пары  есть элементы динамы
есть элементы динамы
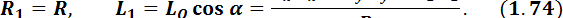
Линия, по которой направлена сила динамы  , назывется центральной винтовой осью. Во всех точках винтовой оси, принятых за центры приведения, система сил приводится к одной и той же динаме. Расстояние от центра приведения О до центральной винтовой оси
, назывется центральной винтовой осью. Во всех точках винтовой оси, принятых за центры приведения, система сил приводится к одной и той же динаме. Расстояние от центра приведения О до центральной винтовой оси

1.5.4. Уравнение центральной винтовой оси
 Предположим, что в центре приведения, принятом за начало координат, получены главный вектор
Предположим, что в центре приведения, принятом за начало координат, получены главный вектор  с проекциями на оси координат
с проекциями на оси координат  и главный момент
и главный момент 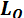 с проекциями
с проекциями 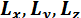 . При приведении системы сил к центру приведения
. При приведении системы сил к центру приведения  (рис. 1.25) получаем динаму с главным
(рис. 1.25) получаем динаму с главным
Рис. 1.25 вектором  и главным
и главным
моментом  . Векторы
. Векторы  и
и  , как образующие динаму, параллельны и поэтому могут отличаться только скалярным множителем
, как образующие динаму, параллельны и поэтому могут отличаться только скалярным множителем  . Имеем
. Имеем
 (1.76)
(1.76)
так как  . Главные моменты
. Главные моменты  и
и 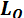 , согласно (1.62) удовлетворяют соотношению
, согласно (1.62) удовлетворяют соотношению
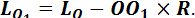 (1.77)
(1.77)
Подставляя  из (1.77) в (1.76), получим
из (1.77) в (1.76), получим
 (1.78)
(1.78)
Координаты точки  , в которой получена динама, обозначим x, y, z. Учитывая это, (1.78) можно выразить в форме
, в которой получена динама, обозначим x, y, z. Учитывая это, (1.78) можно выразить в форме
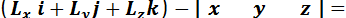

где  – единичные векторы осей координат, а векторное произведение
– единичные векторы осей координат, а векторное произведение  представлено определителем. Векторное уравнение (1.79) эквивалентно трем скалярам, которые можно представить в виде
представлено определителем. Векторное уравнение (1.79) эквивалентно трем скалярам, которые можно представить в виде

Линейные для координат x, y, z уравнения (1.80) являются уравнениями прямой линии – центральной винтовой оси. Следовательно, существует прямая, в точках которой система приводится к динаме.
1.5.5. Теорема о моменте равнодействующей силы
(теорема Вариньона)
Для случая, когда любая система сил, приложенных к твердому телу, плоская или пространственная, приводится к равнодействующей силе, часто применяют теорему Вариньона.
Векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки.
Пусть на твердое тело действует любая система сил 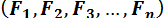 (рис. 1.26), имеющая равнодействующую
(рис. 1.26), имеющая равнодействующую  есть
есть
 (1.81)
(1.81)
Добавим к заданной системе сил ее уравновешивающую силу 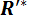 , которая равна по модулю, но противоположна по направлению равнодействующей силе
, которая равна по модулю, но противоположна по направлению равнодействующей силе  и имеет с ней общую линию действия. Тогда
и имеет с ней общую линию действия. Тогда
 ,
,
 т. е. при добавлении к системе сил уравновешивающей силы, согласно определению уравновешивающей силы, образуется новая система сил, эквивалентная нулю и, следовательно,
т. е. при добавлении к системе сил уравновешивающей силы, согласно определению уравновешивающей силы, образуется новая система сил, эквивалентная нулю и, следовательно,
удовлетворяющая условиям равновесия системы сил, приложенных к твердому телу. В частности, сумма векторных моментов сил этой новой системы сил относительно любой точки О равна нулю: Рис. 1.26
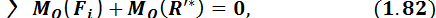
но
 (1.83)
(1.83)
так как 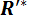 и
и  две равные и противоположно направленные силы, действующие вдоль одной прямой. Подставляя (1.83) в (1.82), получаем
две равные и противоположно направленные силы, действующие вдоль одной прямой. Подставляя (1.83) в (1.82), получаем
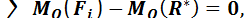
откуда следует теорема Вариньона

Если правую и левую части векторного равенства (1.84) спроектировать на произвольную ось Oz, проходящую через точку О, то, учитывая связь момента силы относительно оси с проекцией векторного момента относительно точки на оси, получим теорему Вариньона относительно оси Oz:
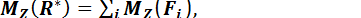 (1.85)
(1.85)
т. е. момент равнодействующей силы относительно произвольной оси равен сумме моментов сил системы относительно той же оси.
Для случая плоской системы сил, если точку О выбрать в плоскости действия сил из (1.84), получаем
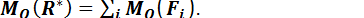 (1.86)
(1.86)
Это теорема Вариньона для плоской системы сил.
Алгебраический момент равнодействующей плоской системы сил относительно любой точки, лежащей в плоскости действия сил, равен сумме алгебраических моментов всех сил этой системы относительно той же точки.
Тема 1.6. Плоская система сил
Плоская система сил является частным случаем произвольной пространственной системы сил.
1.6.1. Частные случаи приведения
1. При приведении системы сил к центру, главный вектор 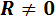 , а главный момент
, а главный момент 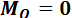 .
.
Такая система сил приводится к равнодействующей, совпадающей по величине и направлению с главным вектором, причем, линия действия равнодействующей проходит через центр приведения.
2. При приведении системы сил к центру главный вектор 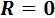 , а главный момент
, а главный момент 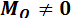 .
.
Система сил приводится к паре сил, алгебраический момент которой равен главному моменту системы сил относительно центра приведения.
3. При приведении системы сил к центру главный вектор 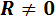 и главный момент
и главный момент 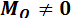 .
.
 Главный момент для такой плоской системы сил перпендикулярен главному вектору, следовательно, такую систему можно привести к одной равнодействующей силе
Главный момент для такой плоской системы сил перпендикулярен главному вектору, следовательно, такую систему можно привести к одной равнодействующей силе  (см. п. 1.5.3).
(см. п. 1.5.3).
Равнодействующая по величине и направлению совпадает с главным вектором, но ее линия действия отстоит на расстоянии  (рис. 1.27) от первоначального центра Рис.1.27
(рис. 1.27) от первоначального центра Рис.1.27
приведения.
1.6.2. Статические определимые и статически неопределимые задачи
Задачи, в которых число неизвестных не превосходит числа независимых уравнений для данной системы сил, приложенных к твердому телу, называют статически определимыми.
Если число неизвестных окажется больше числа независимых уравнений равновесия системы сил, то такие задачи называются статически неопределимыми.
Для любой произвольной плоской системы сил, приложенных к твердому телу, должно быть не больше трех неизвестных, так как уравнений равновесия три.
Статически неопределимые задачи нельзя решить методами статики без учёта деформации тела. Такие задачи рассматриваются в курсах сопротивления материалов, строительной механики и других прикладных дисциплинах.
1.6.3. Равновесие системы тел
Силы, действующие на конструкцию, состоящую из нескольких абсолютно твердых тел, можно разделить на внешние и внутренние.
Внешними называются силы, с которыми на рассматриваемую конструкцию действуют тела, не входящие в эту конструкцию.
Сюда относятся реакции связей, за исключением сил взаимодействия в местах сочленения тел конструкции. Силы тяжести для любой системы тел, в которую не входит Земля, являются внешними.
Внутренними называются силы взаимодействия между телами, входящими в конструкцию.
Основным способом решения задач на равновесие конструкции, состоящей из нескольких тел, является метод расчленения. Сущность этого метода заключается в том, что наряду с рассмотрением конструкции в целом, можно расчленить её на отдельные твердые тела и рассматривать равновесие этих тел в отдельности.
При расчленении конструкции следует принимать во внимание аксиому о силах действия и противодействия.
Для системы n тел можно составить 3n уравнений равновесия и, следовательно, определить 3n неизвестных.
1.6.4. Распределенные силы
В статике рассматривают силы, приложенные к твердому телу в какой-либо его точке, и поэтому такие силы называют сосредоточенными. В действительности, обычно силы бывают приложены к какой-либо части объема тела или его поверхности, а иногда к некоторой части линии. Так как все аксиомы и теоремы статики формулируются для сосредоточенных сил, приложенных к твердому телу, то необходимо рассмотреть способы перехода от распределенных сил к сосредоточенным в простейших, наиболее часто возникающих случаях.
Распределенные силы, прежде всего, характеризуются интенсивностью распределенной силы, т.е. силой, приходящейся на единицу объема, поверхности или длины линии. В основном встречаются параллельные и сходящиеся распределенные силы. К параллельным силам, распределенным по объему телу, относится вес частиц этого тела. Сила давления воды на плотину относится к распределенным параллельным силам по поверхности плотины. Сила тяжести частиц тонкой проволоки характеризуется распределением силы по длине линии.
1. Параллельные силы постоянной интенсивности, распределенные по отрезку прямой линии
Пусть на участке AB прямой линии длинной l распределены параллельные силы, интенсивность которых q постоянна (рис. 1.28, а). Заменим эти распределенные силы сосредоточенными. Для этого отрезок AB разобьем на отрезки достаточно малых размеров по сравнению с его длиной. На каждый такой малый отрезок действует сила 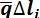 , которую при достаточной малости длины отрезка
, которую при достаточной малости длины отрезка  можно считать сосредоточенной силой. Заменяя полученную таким образом систему сосредоточенных параллельных сил
можно считать сосредоточенной силой. Заменяя полученную таким образом систему сосредоточенных параллельных сил 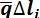 одной равнодействующей силой, получим
одной равнодействующей силой, получим
 (1.87)
(1.87)
Равнодействующая  параллельна распределенным силам и приложена, вследствие симметрии распределения сил, в середине отрезка АВ.
параллельна распределенным силам и приложена, вследствие симметрии распределения сил, в середине отрезка АВ.
Если параллельные силы постоянной интенсивности q распределены по отрезку прямой, наклоненному к распределенным силам, то модуль равнодействующей  таких сил равен ql. Линия действия ее, параллельная распределенным силам, проходит через середину отрезка (рис. 1.28 б). Модуль равнодействующей в этом случае не равен площади параллелограмма, образованного прямой АВ и распределенными силами.
таких сил равен ql. Линия действия ее, параллельная распределенным силам, проходит через середину отрезка (рис. 1.28 б). Модуль равнодействующей в этом случае не равен площади параллелограмма, образованного прямой АВ и распределенными силами.

Рис.1.28
2. Параллельные силы, распределенные по отрезку прямой с интенсивностью, изменяющейся по линейному закону
Рассмотрим распределенные силы, изменяющиеся по линейному закону (рис. 1.29, а). Обычно считают, что такие силы распределены по треугольнику. Параллельные распределенные по треугольнику силы приводятся к равнодействующей  по модулю равной
по модулю равной

где 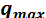 – наибольшая интенсивность силы. Точка приложения С равнодействующей силы расположена на расстоянии
– наибольшая интенсивность силы. Точка приложения С равнодействующей силы расположена на расстоянии 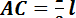 .
.
Это легко можно проверить путем интегрирования с применением теоремы Вариньона.
Если параллельные силы с интенсивностью, изменяющейся по линейному закону, распределены по отрезку прямой, наклоненному к направлению сил (рис. 1.29, б), то их равнодействующая  и делит отрезок АВ так же, как и в случае, когда распределенные силы перпендикулярны отрезку АВ. Величина равнодействующей в этом случае не равна площади треугольника образованного отрезком прямой АВ и распределенными силами.
и делит отрезок АВ так же, как и в случае, когда распределенные силы перпендикулярны отрезку АВ. Величина равнодействующей в этом случае не равна площади треугольника образованного отрезком прямой АВ и распределенными силами.
 б
б
Рис.1.29
В более сложных случаях распределенных сил равнодействующую силу и ее точку приложения обычно определяют путем интегрирования и применением теоремы Вариньона.
1.6.5. Реакция заделки
Рассмотрим балку АВ, один конец которой А заделан в стену (рис. 1.30). Такое крепление конца балки называют заделкой в точке А. Пусть на балку действует система сил  . Выясним, какие силы следует приложить в точке А балки, если часть балки, находящуюся в стене, отбросить.
. Выясним, какие силы следует приложить в точке А балки, если часть балки, находящуюся в стене, отбросить.
К части балки, находящейся в стене, при освобождении ее от заделки приложены распределенные силы реакции. Приведя силы к точке А (рис. 1.31), получим силу  и пару сил с моментом
и пару сил с моментом  . Момент
. Момент  называют моментом заделки. Силу и момент Силу и момент пары сил представляем в виде разложения по осям координат
называют моментом заделки. Силу и момент Силу и момент пары сил представляем в виде разложения по осям координат


Рис. 1.30 Рис.1.31
 (1.89)
(1.89)
Если на балку действует плоская система сил (рис. 1.32), то заделка создает не только неизвестную по величине и направлению реакцию  но и пару сил с неизвестным алгебраическим моментом
но и пару сил с неизвестным алгебраическим моментом  (рис. 1.33).
(рис. 1.33).
Рис.1.32 Рис.1.33
Тема 1.7. Основные законы трения
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхности соприкосновения возникает сила трения скольжения.
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка.
1.7.1. Трение скольжения
Все поверхности тел в той или иной степени шероховаты и все тела деформируемы. В связи с этим сила реакции  шероховатой поверхности при равновесии тела зависит от активных сил не только по числовой величине, но и по направлению (рис. 1.34).Если силу реакции
шероховатой поверхности при равновесии тела зависит от активных сил не только по числовой величине, но и по направлению (рис. 1.34).Если силу реакции  шероховатой поверхности разложить на составляющие, одна из которых
шероховатой поверхности разложить на составляющие, одна из которых  направлена по общей нормали к поверхности соприкосновения, а другая
направлена по общей нормали к поверхности соприкосновения, а другая  находится в касательной плоскости к
находится в касательной плоскости к
 Рис.1.34 этой поверхности, то составляющая
Рис.1.34 этой поверхности, то составляющая  силы реакции является силой трения скольжения, а составляющая
силы реакции является силой трения скольжения, а составляющая  нормальной реакцией.
нормальной реакцией.
В теоретической механике обычно рассматривается только сухое трение между поверхностями тел, т. е. такое трение, когда между ними нет смазывающего вещества. Для сухого трения надо различать трение скольжения при покое и равновесии тела и трение скольжения при движении одного тела по поверхности другого. При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила вычисляется по формуле
 (1.90)
(1.90)
Аналогично, при выбранном направлении нормальная реакция выражается через заданные силы:
 (1.91)
(1.91)
В 1781г. Кулон установил основные приближенные законы для сухого трения скольжения при покое.
Законы Кулона
1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Сила трения зависит от активных сил, и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т. е.