Задачи аппроксимации функции

Лекция 5

2018/2019 уч. г.

 

Раздел 2. Интерполирование функций. Приближенное дифференцирование и интегрирование функций.

 

Тема 6. Интерполирование функций

Лк –2 ч., ПЗ – 6 ч., СРС – 14 ч.

 

1. Основные понятия теории приближения функций. Постановка задачи аппроксимации функции.

2. Интерполирование с помощью многочленов.

3. Интерполяционная формула Лагранжа.

4. Интерполяционные формулы Ньютона.

4.1. Конечные разности функций.

4.2. Первая интерполяционная формула Ньютона.

4.3. Вторая интерполяционная формула Ньютона.

5. Оценка погрешностей интерполяционных формул.

 

Основные понятия теории приближения функций. Постановка

задачи аппроксимации функции

 

В практической деятельности весьма часто используются математические модели, отражающие зависимость одних величин от других. В общем случае эти модели принято записывать в виде

.

В математике величину y называют функцией, а 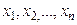- независимыми переменными или аргументами.

В научных исследованиях через y обычно обозначают параметр изучаемого объекта (явления, устройства, процесса и т.п.), который характеризует состояние этого объекта, изменение состояния объекта, например, во времени и т. д. При этом величины 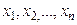называют факторами, которые определяют то или иное состояние объекта, его поведение.

Используются три способа задания функции: аналитический, графический и табличный. Каждый из этих способов имеет свои достоинства и недостатки. Вместе с тем, несмотря на различные формы представления информации о зависимости функции от ее аргументов приведенными способами, их объединяет общий недостаток. Он заключается в том, что не всегда удается получить значение функции y для заданных значений аргументов, даже когда он один.

Например, математическая модель представляет собой нелинейное уравнение или систему уравнений, или представлена в виде дифференциального уравнения , в котором искомая функция y находится под знаком дифференциала. В этих случаях для нахождения значения функции y необходимо применять методы решения этих математических моделей.

При задании функции графическим методом ее значение может быть определено с недостаточно требуемой по условиям задачи точностью. При табличном способе задания функции может отсутствовать ее значение для нужного значения аргумента.

В этих случаях возникает задача аппроксимации (приближения) функции, которая формулируется в виде:

Пусть для ряда значений аргумента x: x ₀, x ₁, x ₂ ,…, x_n получены значения функции : y ₀, y ₁, y ₂ ,…, y_n [1].

Необходимо определить значения функции в точках x, отличных от x ₀, x ₁, x ₂ ,…, x_n.

Основу решения этой задачи составляет следующая идея. Используя имеющуюся информацию о значениях функции в точках x: x ₀, x ₁, x ₂,…, x_n, построить другую функцию , отклонения значений которой от значений функции в заданной области изменения ее аргумента x являются наименьшими. При этом определение значений функции должно выполняться по более простым правилам, чем при нахождении значений y ₀, y ₁, y ₂,…, y _n функции .

В этой задаче функцию называют аппроксимирующей, а - аппроксимируемой функцией.

При реализации этой идеи рассматриваются четыре вопроса.

1. В какой форме задана информация о функции : аналитической, графической, табличной?

2. Какими функциями должна быть аппроксимирована функция ?

3. Какому критерию согласия должна удовлетворять близость функции к функции ?

4. Какова погрешность приближенного значения по отношению к точному значению ?

При рассмотрении первого вопроса, в дальнейшем будем полагать, что функция задана своими значениями в точках (узлах) x интервала [ a, b ]:

x: a ≤ x ₀ < x ₁ < x ₂ <…< x_n ≤ b,

на котором она непрерывна и имеет достаточное количество своих непрерывных производных.

При решении вопроса о классе аппроксимирующих функциях исходят из двух требований. Во-первых, аппроксимирующая функция должна отражать характерные свойства аппроксимируемой , во-вторых, должна быть удобной в обращении, т.е. не допускать сложных и громоздких вычислений ее значений.

В численном анализе широкое применение имеют три класса аппроксимирующих функций. Первый составляют функции вида 1, x, x ²,…, xⁿ, линейные комбинации которых порождают все многочлены степени не выше n.

Второй класс составляют тригонометрические функции sin a_ix иcos a_ix, порождающие ряды Фурье и интеграл Фурье[2]. Третий класс это экспоненциальные функции , с помощью которых описываются явления распада и накопления, часто встречающиеся в реальных ситуациях (например, убывание знаний без их закрепления применением).

Вопрос о близости аппроксимирующей и аппроксимируемой функции по существу сводится к выбору такой функции , чтобы ее отклонения от заданной функции на множестве точек x_i было наименьшим.

Например, пусть в качестве аппроксимирующей функции взят многочлен вида

.

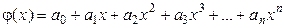При решении вопроса о близости такой функции к заданной необходимо подобрать такие коэффициенты a ₀, a ₁, a ₂,…, a_n, чтобы отклонения от в узлах x ₀, x ₁, x ₂, …, x_n были наименьшими.

Решение вопроса о погрешности приближенного значения по отношению к значению зависит от таких факторов, как расположение узлов x_i, используемый класс функций для построения , выбранный критерий согласия и . Поэтому в самом общем случае этот вопрос является открытым и подлежит исследованию для каждого конкретного аппроксимационного процесса.

При решении задачи аппроксимации функций используются следующие понятия.

Точечная аппроксимация. Это аппроксимация, при которой приближение строится на дискретном множестве аргумента x: x ₀, x ₁, x ₂ ,…, x_n.

При построении аппроксимирующей функции на непрерывном множестве точек отрезка [ a, b ] аппроксимация называется непрерывной (интегральной).

При точечной аппроксимации важное значение имеет частный случай, когда аппроксимирующая функция подбирается такой, значения которой в узлах x ₀, x ₁, x ₂ ,…, x_n совпадают со значениями заданной функции в этих узлах. Такой способ аппроксимации, основанный на критерии совпадения значений функций и 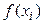в узлах x_i, называется интерполированием (интерполяцией). Точки x_i называются узлами интерполяции.

Если аппроксимирующая функция совпадает с 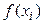во всех узлах x_i рассматриваемого интервала [ a, b ], то такая интерполяция является глобальной интерполяцией. Если аппроксимирующая функция строится для разных частей интервала [ a, b ], то такая интерполяция является локальной интерполяцией.

В случае, когда приближенное значение функции определяется для аргумента x, принадлежащего отрезку [ a, b ], то такую задачу определения значения функции называют интерполяцией в узком смысле. Если же аргумент x находится вне отрезка [ a, b ], то поставленная задача называется экстраполированием.

 

2. Интерполирование с помощью многочленов

 

Выше было отмечено, интерполированием является аппроксимация, когда аппроксимирующая функция подбирается такой, значения которой в узлах x ₀, x ₁, x ₂ ,…, x_n совпадают со значениями заданной функции в этих узлах. При этом точки x_i называются узлами интерполяции.

Примем в качестве аппроксимирующей функции алгебраический многочлен, представляющий собой линейную комбинацию функций вида 1, x, x ²,…, xⁿ. В этом случае функция обычно обозначается через P_n (x) и записывается в виде

. (1)

Закономерен вопрос, существует ли такой многочлен P_n (x) степени не выше n, значения которого совпадают со значениями функции в узлах x ₀, x ₁, x ₂ ,…, x_n, т.е.

(2)

и является ли он единственным.

Ответ на этот вопрос дает следующая теорема.

Теорема. Пусть:

1) на отрезке [ a, b ] заданы узлы x: x ₀, x ₁, x ₂ ,…, x_n, для которых имеет место неравенство

a ≤ x ₀ < x ₁ < x ₂ <…< x_n ≤ b; (3)

2) заданы в узлах x_i значения y_i (i = 0, 1, 2, 3,, n) некоторой функции .

Тогда существует и притом единственный многочлен P_n (x) степени не выше n, принимающий в узлах x_i заданные значения y_i.

Для вычисления неизвестных коэффициентов a ₀, a ₁, a ₂, a ₃,…, a_n многочлена P_n (x)

подставим значения y_i для каждого узла x_i и потребуем выполнения условия: ; ; ; … .

В результате получим систему линейных уравнений относительно неизвестных a ₀, a ₁, a ₂, a ₃,…, a_n:

(4)

Определитель этой системы

(5)

является определителем Вандермонда, который отличен от нуля, если при . Это условие выполняется для заданных узлов (3). Поэтому система (4) имеет единственное решение и, следовательно, многочлен P_n (x) существует и является единственным.

Примечание. 1. Многочлен P_n (x), удовлетворяющий условиям (2), называется интерполяционным многочленом, а метод его построения -методом неопределенных коэффициентов. Чтобы указать зависимость многочлена P_n (x) от функции его часто обозначают .

2. Поскольку интерполяционный многочлен P_n (x) совпадает с 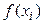во всех узлах x_i рассматриваемого интервала [ a, b ], то такая интерполяция является глобальной интерполяцией.