Кривые второго порядка.
Эллипс
Пусть в плоскости фиксированы точки F1 и F2, эллипсом называется геометрическое место точек, таких, что сумма расстояний от них до F1 и F2, называемыми фокусами эллипса, есть постоянная величина, обозначаемая через a*2.
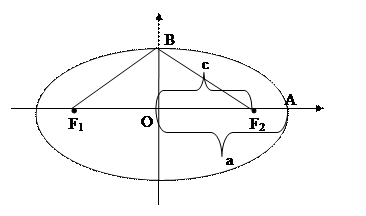
Каноническая система координат эллипса.
· Проведем прямую через фокусы эллипса F1 и F2.(Ox)
· Ориентируем прямую от F1 к F2.
· Середину F1F2 обозначим через О.
· Проведем прямую Oy перпендикулярную Ox.
· Ориентируем прямую так, чтобы система была положительно ориентированна.
Точки пересечения с осями координат – вершины эллипса
Расстояние от фокуса до центра обозначим через с.
АF1 + АF2 =2*а
OA=а – большая полуось эллипса
Рассмотрим треугольник F1F2В – равнобедренный
F1В + F2В=2*а => F1В=F2В=а
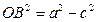 , OB=b – длинна малой полуоси (
, OB=b – длинна малой полуоси ( )
)
Эксцентриситетом эллипса называется число 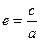 . При е=0 это окружность, а при е=1 это прямая.
. При е=0 это окружность, а при е=1 это прямая.
Директрисами эллипса называется прямые имеющие уравнения 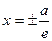
Уравнение эллипса.
Эллипс в канонической системе координат имеет уравнение 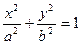 - каноническое уравнение.
- каноническое уравнение.
Симметрия эллипса
1. Эллипс симметричен относительно оси оХ.
2. Эллипс симметричен относительно оси оY.
3. Эллипс симметричен относительно центра координат.
Пусть эллипс задан каноническим уравнением, точка P(α, β) принадлежит эллипсу. Тогда касательная в точке Р имеет вид: 
Оптическое свойство эллипса.
Если из одного фокуса эллипса выпустить луч света, то отразившись от эллипса луч попадет в другой фокус.
Гипербола.
Пусть в плоскости даны точки F1 и F2, которые называются фокусами, гиперболой называется геометрическое место точек, таких что модуль разности расстояний от точки до фокусов, есть постоянная величина, обозначаемая через 2*а.

Каноническая система координат гиперболы.
· Проведем прямую через фокусы эллипса F1 и F2.(Ox)
· Ориентируем прямую от F1 к F2.
· Середину F1F2 обозначим через О.
· Проведем прямую оY перпендикулярную Ox.
· Ориентируем прямую так, чтобы система была положительно ориентированна.
F1F2=2*с=> OF1=c
Точки пересечения с осями
OF1=|F1A-F2A|=2*a
Расстояние от центра до вершины равно а(как и для эллипса, но a<c)
Введем b: 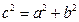
Эксцентриситетом гиперболы называется число e, определенное как 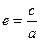 , 1<e<∞
, 1<e<∞
Полученный прямоугольник называется основанием прямоугольной гиперболы.
Прямые, лежащие на диагоналях основного прямоугольника асимптоты гиперболы bx+ay=0;bx-ay=0.
Директрисами гиперболы называются прямые с уравнениями 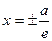 .
.
Каноническое уравнение гиперболы.
Гипербола в канонической для нее системе координат имеет уравнение: 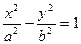
Симметрия гиперболы.
1. Относительно оси Ох.
2. Относительно оси Oy.
3. Относительно центра системы координат.
Касательная.
Пусть задана парабола 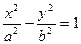 и точка Р(α,β), тогда уравнение касательно в точке Р:
и точка Р(α,β), тогда уравнение касательно в точке Р:
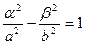
Оптическое свойство гиперболы.
Если из одного из фокусов гиперболы выпустить луч света, то после отражения от гиперболы, луч пойдет по прямой, проходящей через второй фокус.
Парабола.
Пусть дана прямая L, называемая директрисой, и точка F, называемая фокусом, параболой называется геометрическое место точек таких, что расстояние от прямой L до точки F равно расстоянию от точки до фокуса.
Каноническая система параболы.
1. Через точку F проведем прямую перпендикулярную L
2. Ориентируем её от L к F.
3. Отметим точку О – середину отрезка LF.
|
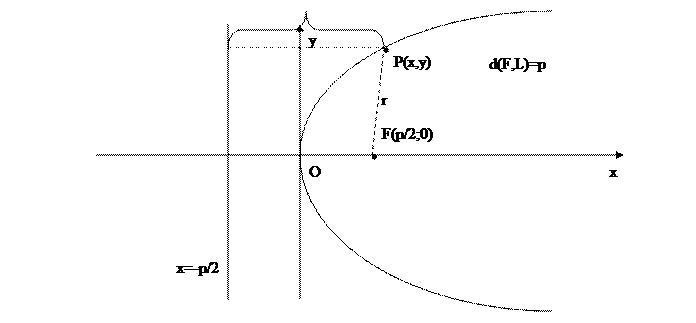
Каноническое уравнение параболы.
В канонической системе координат парабола имеет уравнение  .
.
Эксцентриситет параболы по определению равен еденице.
Оптическое свойство параболы.
Если из фокуса параболы выпустить световые лучи, тогда отразившись от параболы они образуют пучок лучей параллельных оси ОХ.
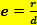
где r- расстояние от точки A до фокуса и d-расстояние от точке A до директрисы соответствующей рассматриваемому фокусу.
__________________________________________________________________________
Собственные вектора и собственные значения.
Вектор 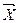 называется собственным значением матрицы А, если А
называется собственным значением матрицы А, если А 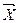 =λ
=λ 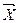 , при это λ называется собственным значением матрицы А соответствующем собственному вектору.
, при это λ называется собственным значением матрицы А соответствующем собственному вектору.