Контрольная работа №4
Найти общее решение дифференциального уравнения. Сделать проверку.
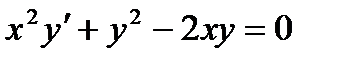
Разделим обе части уравнения на х2:
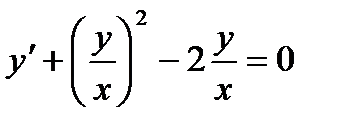
Сделаем замену: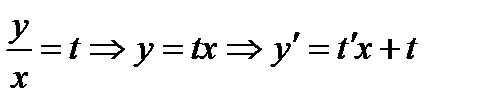 
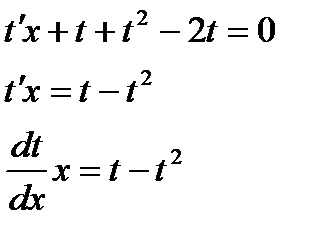
Решим уравнение, разделив переменные: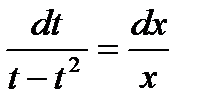 
;
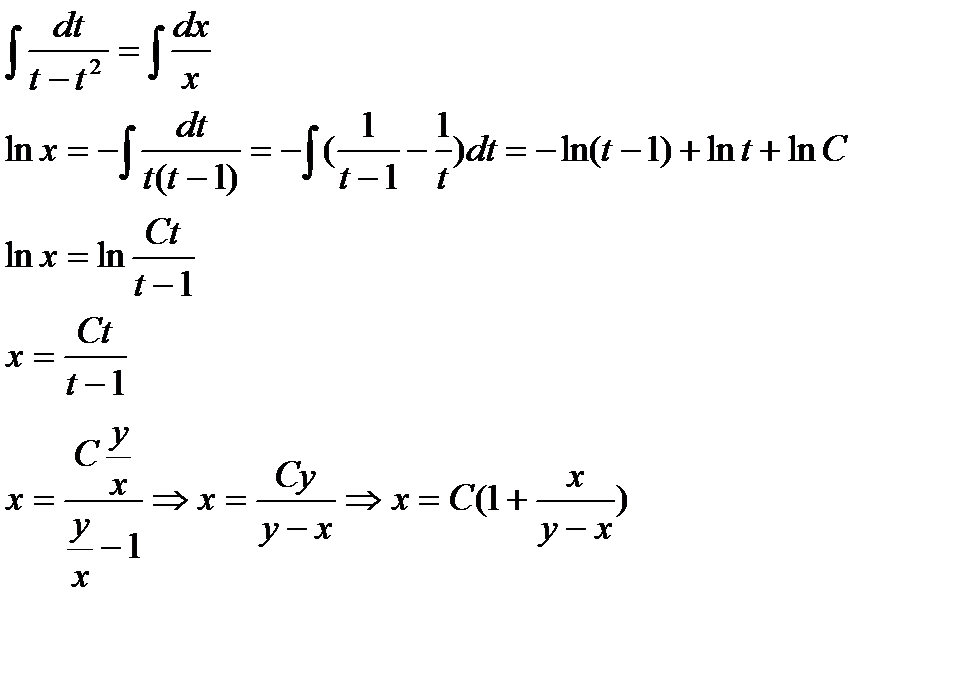
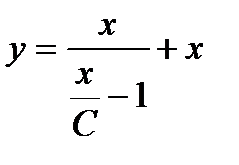– общее решение дифференциального уравнения.
Сделаем проверку:
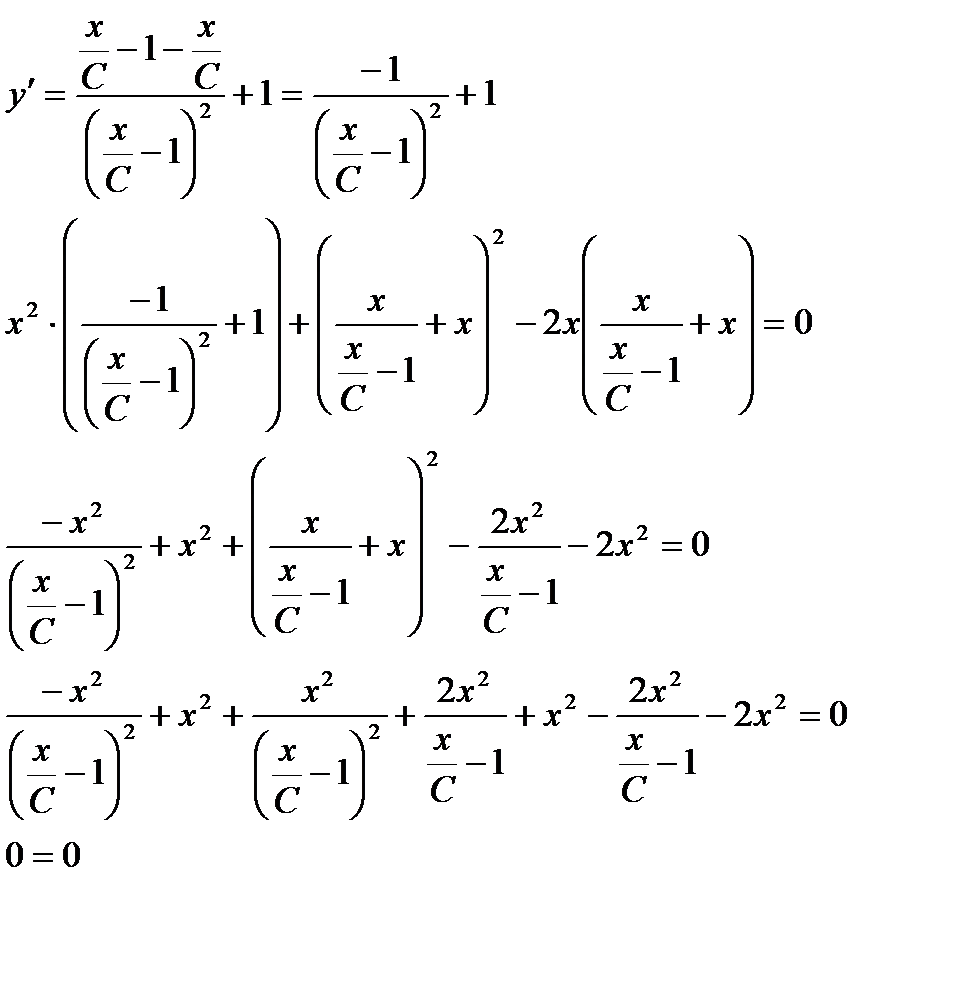
Решение верное.
Найти общее решение линейного дифференциального уравнения. Сделать проверку.
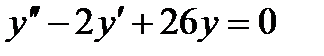
Его характеристическое уравнение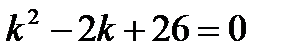 
имеет корни:
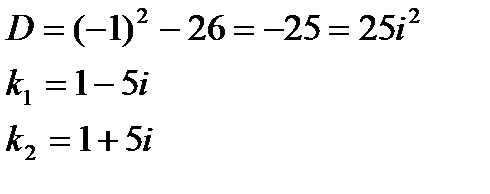
В этом случае общее решение однородного уравнения имеет вид:
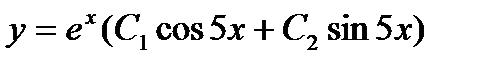
Сделаем проверку:
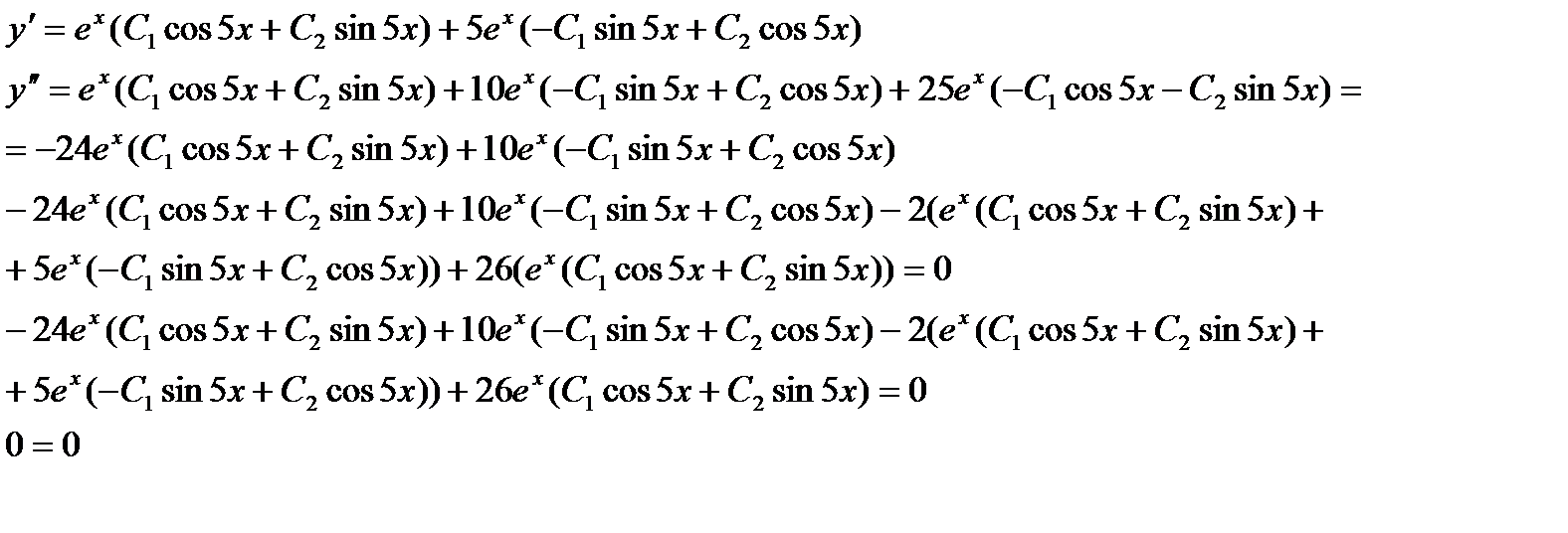
Решение верное.
Написать простейшую формулу n-го члена по указанным членам
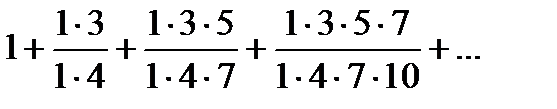
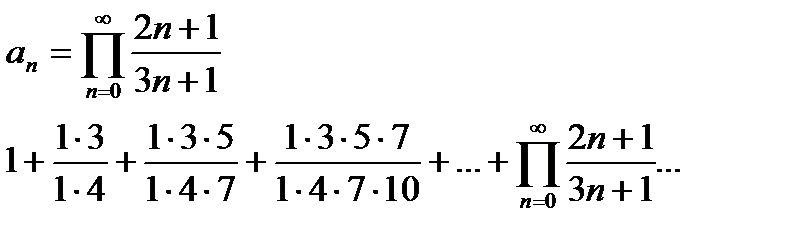
11.2.49. При каких значениях р из множества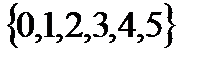 
заданный ряд сходится условно?
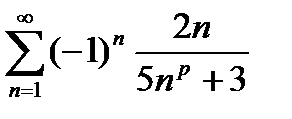
Ряд сходится абсолютно, если сходится ряд из модулей: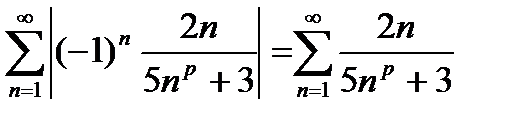 
Воспользуемся признаком сравнения, возьмем ряд для сравнения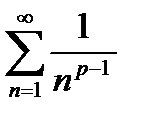 
, который сходится при р=3 или р=4 или р=5, (т.к. несобственный интеграл 
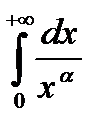сходится при α>1). Найдем предел отношений этих рядов:
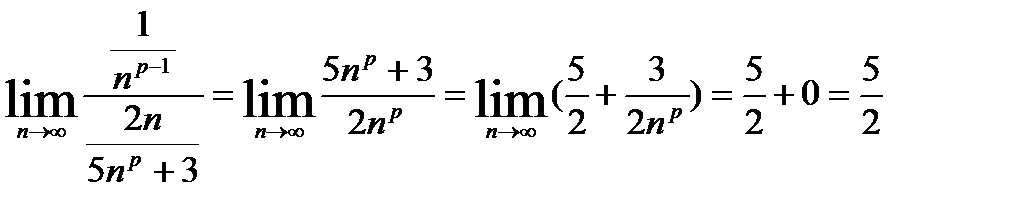
Предел отношений должен быть конечен, чтобы оба ряда сходились одновременно и ряд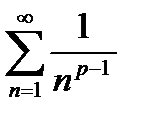 
должен сходится.
Ряд будет сходится абсолютно, если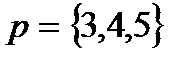 
. Значит, ряд может сходиться условно только при 
.
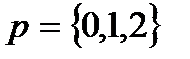Рассмотрим признак Лейбница для знакочередующихся рядов.
1) 
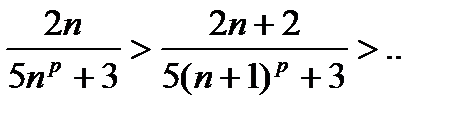
2) 
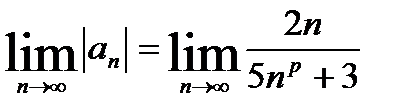должен быть равен нулю. Это произойдет, если степень знаменателя будет больше степени числителя, т.е. больше 1.
Значит, данный ряд сходится условно только для р=2.
Определить область сходимости степенного ряда
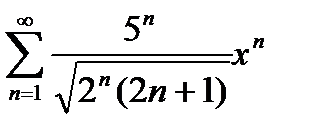
Найдем радиус сходимости данного ряда по формуле Коши-Адамара:
.
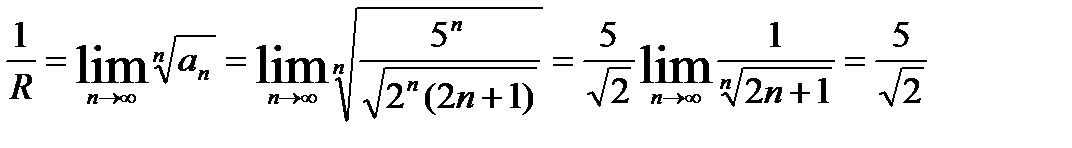Значит, R=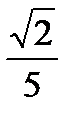 
. Тогда, интервал сходимости будет 
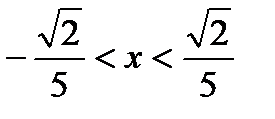или (- 
; 
).
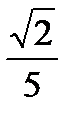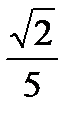Рассмотрим сходимость данного ряда на концах интервала сходимости.
Пусть х = -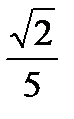 
. Тогда получим ряд 
.
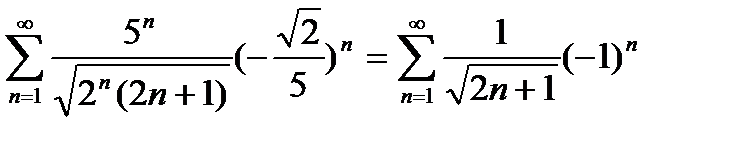Этот ряд сходится по признаку Лейбница, т.к.:
1) 
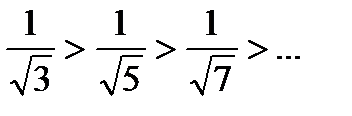
2) 
.
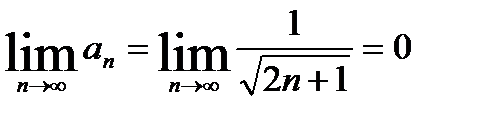А это говорит о том, что данный ряд сходится при х=-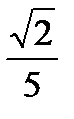 
.
Пусть х =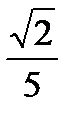 
. Тогда получим ряд 
.
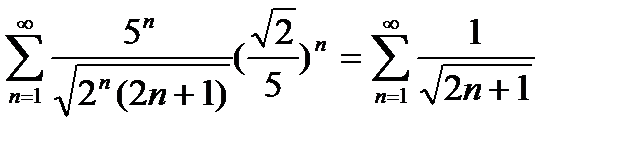Воспользуемся признаком сравнения, возьмем ряд для сравнения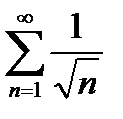 
, который расходится, (т.к. несобственный интеграл 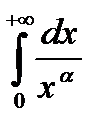сходится при α>1). Найдем предел отношений этих рядов:
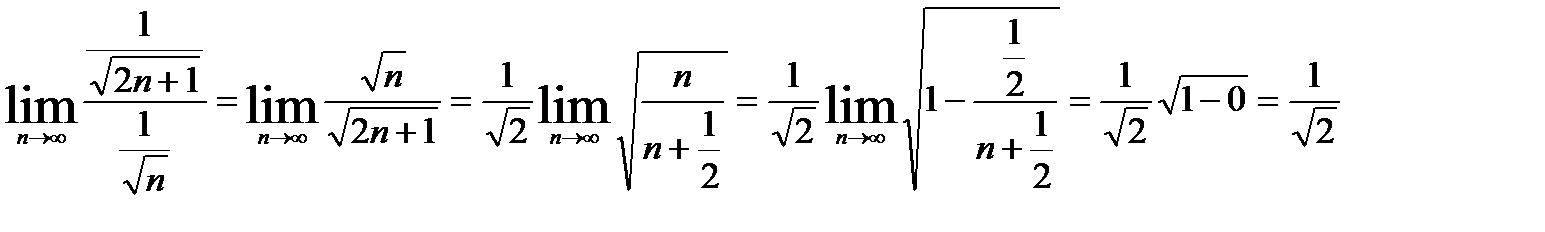
Т.к. предел отношений конечен, то оба ряда расходятся одновременно.
Значит, область сходимости интервал [- 
; 
).
11.3.79 Разложить функцию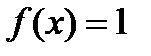 
в ряд по синусам в ряд Фурье на отрезке 
.
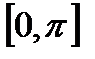Вычислим коэффициенты:
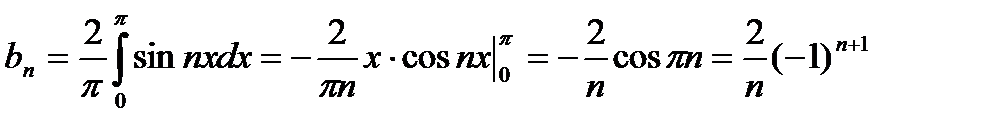
Соблюдаются условия Дирехле:
1) В каждой точке непрерывности х функции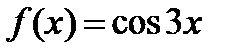 
ряд Фурье сходится к значению 
;
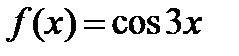2) В каждой точке разрыва хi функции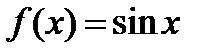 
ряд Фурье сходится к значению
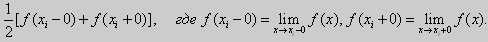
Таким образом ряд Фурье имеет вид:
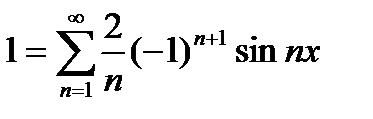
Контрольная работа 5
В ящике лежат яблоки и груши: 80 яблок и 90 груш. С вероятностью 0,8 яблоко хорошее, а груша -0,6. Взятый фрукт хороший. Какова вероятность того, что это яблоко.
Обозначим через А событие «взятый фрукт хороший». Фрукт может быть грушей (событие В1), или яблоком (событие В2). Вероятность того, что это груша равна Р(В1)=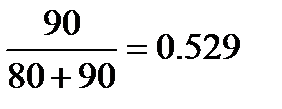 
. Вероятность того, что это яблоко равна Р(В2)= 
.
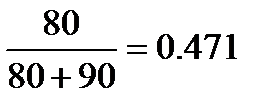Условная вероятностьтого, что выбранная груша хорошая равна,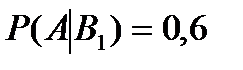 
. Условная вероятность того, что выбранное яблоко хорошее равна, 
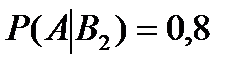. Искомая вероятность того, что взятый фрукт хороший по формуле полной вероятности равна
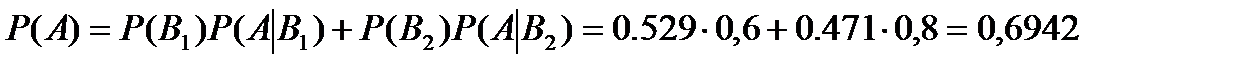
Наугад взятый хороший фрукт оказался яблоком. Вероятность этого по формуле Байеса, равна
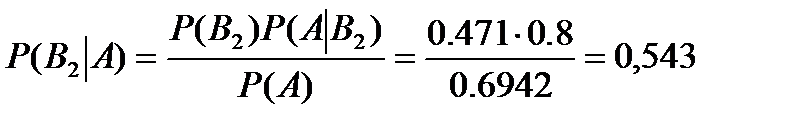
Ответ: вероятность того, что хороший фрукт яблоко равна 0,543.
Вероятность того, что в пакетике с чипсами попадется призовой купон равна 0,1. Х– число пакетиков с купонами среди двух выбранных. Найти дисперсию случайной величины Х.
Условие задачи соответствует проведению n=2 независимых испытаний. Возможные значения Х таковы: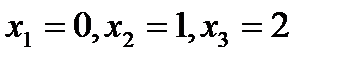 
.
Пусть событие, состоящее в том, что в первом пакетике купон – это событие А1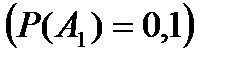 
, во втором пакетике купон – событие А2 
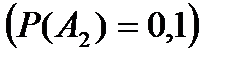.Тогда
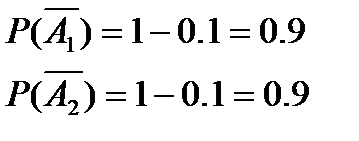
Событие В0, состоящее в том, что число пакетиков с купонами будет равно 0, будет произведением двух несовместных событий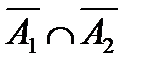 
. Т.е. 
.
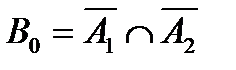Т.к. события А1, А2 и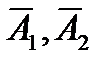 
независимы, то искомая вероятность равна:
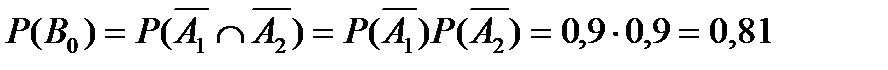
Событие В1, состоящее в том, что только один пакетик будет с купоном, будет суммой двух несовместных событий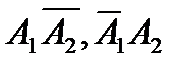 
. Т.е.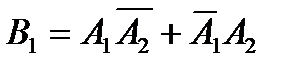 
Т.к. события А1, А2 и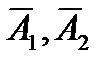 
независимы, то искомая вероятность равна:
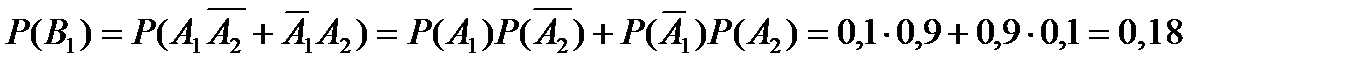
Событие В2, состоящее в том, что два пакетика будут с купоном, будет произведением двух несовместных событий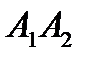 
. Т.е. 
.
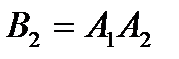Т.к. события А1, А2 и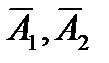 
независимы, то искомая вероятность равна:
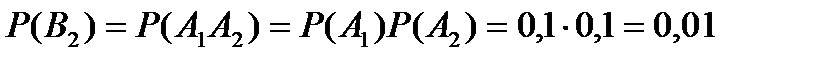
Напишем искомый закон распределения:
| х | |||
| р | 0,81 | 0,18 | 0,01 |
Рассчитаем математическое ожидание и дисперсию
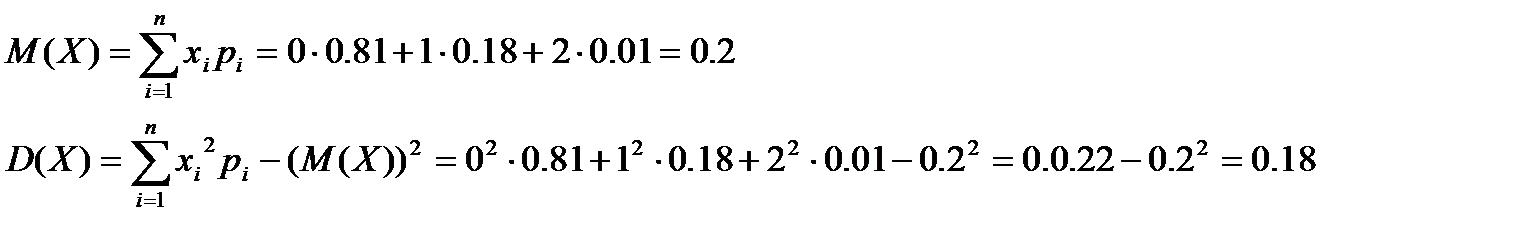
Ответ: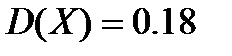 
7.2.49. Задана функция распределения вероятностей F(x) непрерывной случайной величины Х. Требуется:
Найти функцию плотности распределения вероятноcтей f(X).