Определение 4.1. Множество X называют счетным, если можно установить взаимно однозначное отображение  между множеством неотрицательных целых чисел Z0 и множеством X.
между множеством неотрицательных целых чисел Z0 и множеством X.
Определение 4.2. Множество называют не более чем счетным, если оно счетно или конечно.
Определение 4.3. Перечислением или нумерацией множества X называется отображение  множества Z0 на множество X.
множества Z0 на множество X.
Перечисление f определяет на множестве X некоторую бесконечную последовательность 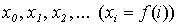 элементов из X такую, что каждый из элементов множества X встречается в этой последовательности, по крайней мере, один раз.
элементов из X такую, что каждый из элементов множества X встречается в этой последовательности, по крайней мере, один раз.
Если отображение f - взаимно однозначно, то f называют перечислением или нумерацией без повторений.
Определение 4.4. Множество X называется эффективно счетным, если существует функция  , устанавливающая взаимно однозначное соответствие между множествами Z0 и X такая, что f и f--1 - вычислимые функции.
, устанавливающая взаимно однозначное соответствие между множествами Z0 и X такая, что f и f--1 - вычислимые функции.
Теорема 4.1. Следующие множества являются эффективно счетными:
а) 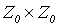 ;
;
б) 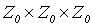 ;
;
в) 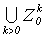 - множество всех конечных последовательностей целых неотрицательных чисел.
- множество всех конечных последовательностей целых неотрицательных чисел.
Доказательство. а) Докажем сначала эффективную счетность множества 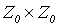 , состоящего из упорядоченных пар (x, y) с целочисленными неотрицательными компонентами x и y. Геометрически это множество представляет целочисленную решетку (рис. 4.1).
, состоящего из упорядоченных пар (x, y) с целочисленными неотрицательными компонентами x и y. Геометрически это множество представляет целочисленную решетку (рис. 4.1).
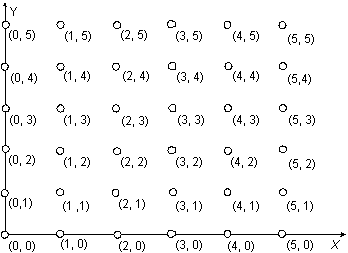
Рис. 4.1. Целочисленная решетка
Перенумеровать точки этой решетки можно различными способами, например, так, как показано на рисунке 4.2.
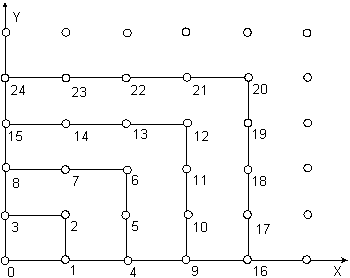
Рис. 4.2. Нумерация точек целочисленной решетки
Предложенная нумерация устанавливает взаимно однозначное отображение 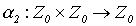 между множествами
между множествами 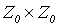 и
и 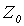 . Алгоритмический характер процесса вычисления значений функции
. Алгоритмический характер процесса вычисления значений функции 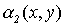 очевиден. Следовательно, по тезису Черча
очевиден. Следовательно, по тезису Черча 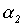 - вычислимая функция.
- вычислимая функция.
Для вычисления значений обратной функции  можно, например, в соответствии с предложенным алгоритмом последовательно нумеровать точки целочисленной решетки до номера z. Пара (x, y) координат точки с номером z является значением обратной функции
можно, например, в соответствии с предложенным алгоритмом последовательно нумеровать точки целочисленной решетки до номера z. Пара (x, y) координат точки с номером z является значением обратной функции  . По тезису Черча
. По тезису Черча  - вычислимая функция.
- вычислимая функция.
Таким образом, множество 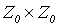 эффективно счетно.
эффективно счетно.
б) Теперь несложно доказать эффективную счетность множества 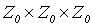 . Для этого определим взаимно однозначное отображение
. Для этого определим взаимно однозначное отображение 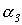 множества
множества  упорядоченных троек неотрицательных целых чисел на множество
упорядоченных троек неотрицательных целых чисел на множество 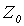 следующим образом
следующим образом 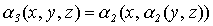 . Из вычислимости функций
. Из вычислимости функций 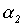 и
и  вытекает вычислимость функций
вытекает вычислимость функций 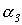 и
и 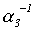 . Поэтому множество
. Поэтому множество 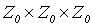 эффективно счетно.
эффективно счетно.
в) Для доказательства эффективной счетности множества всех конечных последовательностей целых неотрицательных чисел 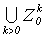 рассмотрим функцию
рассмотрим функцию
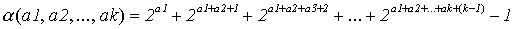 ,
,
сопоставляющую каждому упорядоченному набору (a1, a2,..., ak) из k неотрицательных целых чисел некоторое неотрицательное целое число.
Для доказательства взаимной однозначности функции 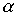 используем тот факт, что у каждого целого числа имеется ровно одно представление в двоичной системе счисления. Запишем значение функции
используем тот факт, что у каждого целого числа имеется ровно одно представление в двоичной системе счисления. Запишем значение функции 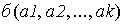 в двоичной системе счисления:
в двоичной системе счисления:
 (*)
(*)
Например,
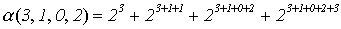 =
=
= 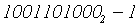 = 616 - 1 = 615;
= 616 - 1 = 615;
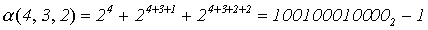 =
=
= 2320 -1 = 2319;
 = 544 -1 = 543;
= 544 -1 = 543;
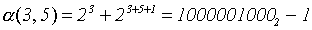 = 520 - 1 = 519;
= 520 - 1 = 519;
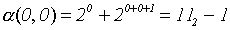 = 3 - 1 = 2;
= 3 - 1 = 2;
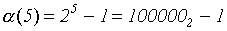 = 32 - 1 = 31;
= 32 - 1 = 31;
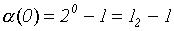 = 1 - 1 = 0.
= 1 - 1 = 0.
Однозначность отображения 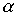 следует из того, что
следует из того, что
 .
.
Так как, кроме того, для любого неотрицательного числа x существует, очевидно, кортеж (c1, c2,..., cn) такой, что 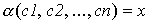 , то функция
, то функция 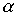 устанавливает взаимно однозначное соответствие между множеством
устанавливает взаимно однозначное соответствие между множеством 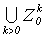 и множеством
и множеством 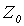 .
.
Покажем, как вычисляются значения обратной функции 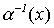 для произвольного неотрицательного числа x.
для произвольного неотрицательного числа x.
В соответствии с формулой (*)
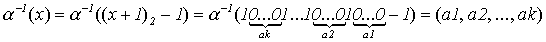 ,
,
где 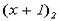 - запись числа x + 1 в двоичной системе счисления.
- запись числа x + 1 в двоичной системе счисления.
Например,
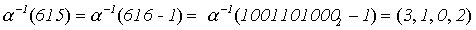 ;
;
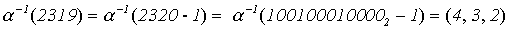 ;
;
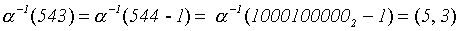 ;
;
 ;
;
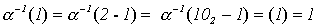 ;
;
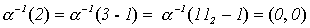 ;
;
 ;
;
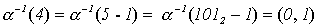 .
.
В силу тезиса Черча функции 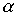 и
и 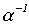 вычислимы. Следовательно,
вычислимы. Следовательно, 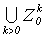 - эффективно вычислимое множество.
- эффективно вычислимое множество.
Теорема 4.2. Множество K команд МНР эффективно счетно.
Доказательство. Множество K команд МНР включает четыре типа команд Z(n), S(n), T(m, n), J(m, n, q), где 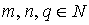 . Определим взаимно однозначное отображение
. Определим взаимно однозначное отображение 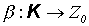 следующим образом:
следующим образом:
 = 4 (n - 1);
= 4 (n - 1);
 = 4 (n - 1) + 1;
= 4 (n - 1) + 1;
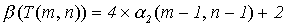 ;
;
 ,
,
где  - отображения, определенные в теореме 4.1.
- отображения, определенные в теореме 4.1.
Так как функции 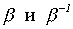 , очевидно, вычислимы, то отсюда вытекает эффективная счетность множества K команд МНР.
, очевидно, вычислимы, то отсюда вытекает эффективная счетность множества K команд МНР.
Теорема 4.3. Множество P всех программ для МНР эффективно счетно.
Доказательство. Пусть 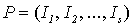 - произвольная программа для МНР. Определим взаимно однозначное отображение
- произвольная программа для МНР. Определим взаимно однозначное отображение 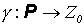 следующим образом:
следующим образом:
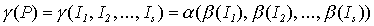 .
.
где  - отображения, определенные в теореме 4.1. Так как функции
- отображения, определенные в теореме 4.1. Так как функции  , очевидно, вычислимы, то отсюда вытекает эффективная счетность множества P всех программ для МНР.
, очевидно, вычислимы, то отсюда вытекает эффективная счетность множества P всех программ для МНР.
Разумеется, существует много других отображений из P в 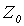 , устанавливающих эффективную счетность множества P. Для нашего изложения подходит любое из таких отображений. Зафиксируем одно из них, например, то которое описано в теореме 4.3.
, устанавливающих эффективную счетность множества P. Для нашего изложения подходит любое из таких отображений. Зафиксируем одно из них, например, то которое описано в теореме 4.3.
Определение 4.5. Число (P) называется геделевым номером программы P или просто номером программы P.
Отображение играет важную роль в теории алгоритмов. Название числа (P) связано с именем К. Геделя, впервые в 1931 году предложившего идею кодирования нечисловых объектов натуральными числами.
Ниже программу P с геделевым номером n будем обозначать  . Из взаимной однозначности отображения следует
. Из взаимной однозначности отображения следует 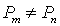 при
при 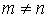 , хотя обе эти программы
, хотя обе эти программы 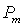 и
и  могут вычислять одну и ту же функцию.
могут вычислять одну и ту же функцию.
Пример 4.1. Найдем геделев номер программы P:
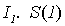 ,
,
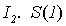 ,
,
вычисляющей функцию f (x) = x + 2.
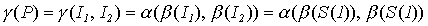 .
.
(S (1)) = 4 (1 - 1) + 1 = 1;
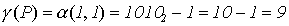 .
.
Пример 4.2. Вычислим программу 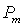 по ее геделеву номеру m.
по ее геделеву номеру m.
1) m = 0.
 ;
; 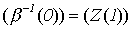 .
.
Следовательно,
 : 1. Z (1).
: 1. Z (1).
2) m = 1.
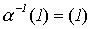 ;
; 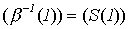 .
.
Следовательно,
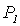 : 1. S (1).
: 1. S (1).
3) m = 2.
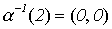 ;
; 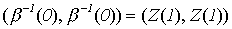 .
.
Следовательно,
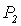 : 1. Z (1),
: 1. Z (1),
2. Z (1).
4) m = 3.
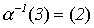 ;
;  .
.
Следовательно,
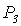 : 1. T (1, 1).
: 1. T (1, 1).
Заметим, что различные программы  и
и 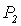 вычисляют одну и ту же функцию f (x) = 0.
вычисляют одну и ту же функцию f (x) = 0.
5. Нумерация вычислимых функций
Определение 5.1. Пусть f - n- местная функция, вычислимая по программе P с геделевым номером m = (P). Число m будем называть индексом функции f. Вычислимую функцию от n переменных с индексом m будем обозначать символом 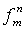 .
.
Из определения 5.1 следует, что каждая n- местная вычислимая функция f представлена в перечислении 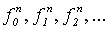
Ниже мы в основном будем рассматривать одноместные вычислимые функции 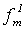 . Для простоты в их обозначении верхний индекс будем опускать.
. Для простоты в их обозначении верхний индекс будем опускать.
Упражнение
5.1. Докажите, что у каждой вычислимой функции имеется бесконечно много индексов.
Приступим теперь к доказательству теоремы о существовании невычислимых функций. Идея доказательства этой теоремы столь же важна, как и результат.
Теорема 5.1. Существует невычислимая всюду определенная функция.
Доказательство. Пусть 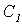 - некоторое перечисление всех вычислимых функций:
- некоторое перечисление всех вычислимых функций:
Положим

Функция g отличается от любой вычислимой функции 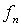 в точке n. Действительно, если функция
в точке n. Действительно, если функция 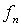 определена в точке n, то
определена в точке n, то 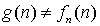 . Если
. Если 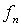 не определена в точке n, то g отличается от
не определена в точке n, то g отличается от 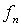 тем, что значение g (n) определено. Таким образом,
тем, что значение g (n) определено. Таким образом, 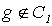 и, следовательно, g - невычислимая всюду определенная функция.
и, следовательно, g - невычислимая всюду определенная функция.
Метод построения функции в теореме 5.1 является примером диагональной конструкции, открытой Кантором. Лежащая в его основе идея является центральной в доказательстве большинства результатов, связанных с вычислимостью функций, и применима к огромному числу ситуаций, возникающих в различных разделах математики.
Поясним, почему для примененного в теореме 5.1 метода выбран термин диагональный. Для этого проиллюстрируем метод построения функции g с помощью следующей бесконечной таблицы:
| 0 | 1 | 2 | 3 | ... | |
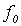
| 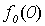
| 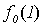
| 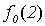
| 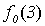
| ... |
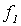
| 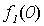
| 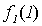
| 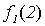
| 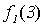
| ... |

| 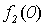
| 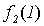
| 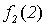
| 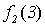
| ... |
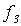
| 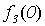
| 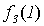
| 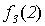
| 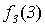
| ... |
| ... | ... | ... | ... | ... | ... |
Рис. 5.1. Диагональная конструкция
При построении функции g для определения значений в точках n выбирались диагональные элементы таблицы 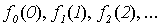 . Выбранные значения изменялись так, чтобы обеспечить отличие g (n) от
. Выбранные значения изменялись так, чтобы обеспечить отличие g (n) от 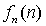 .
.
Очевидно, что новые значения функции можно выбирать сравнительно свободно. Например, функция
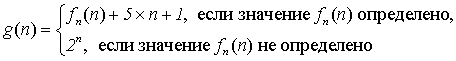
является другой невычислимой всюду определенной функцией.
Проиллюстрируем диагональную конструкцию на примере из теории множеств.
Пример 5.1. Докажем, что множество всех подмножеств множества 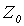 нельзя перечислить (перенумеровать).
нельзя перечислить (перенумеровать).
От противного, пусть 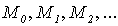 - перечисление всех подмножеств множества
- перечисление всех подмножеств множества 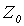 . Определим новое подмножество B множества
. Определим новое подмножество B множества 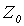 следующим образом:
следующим образом:
 .
.
Очевидно, 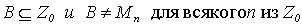 , что противоречит предположению. Поэтому множество всех подмножеств множества
, что противоречит предположению. Поэтому множество всех подмножеств множества 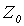 нельзя перечислить.
нельзя перечислить.
Из доказанного вытекает, что множество всех подмножеств множества 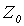 несчетно.
несчетно.
Упражнения
5.2. Используя диагональный метод, докажите что множество всех функций из N в N несчетно (Кантор).
5.3. Докажите, что множество всех невычислимых всюду определенных функций из N в N несчетно.
6. Универсальные программы
В этом разделе мы докажем несколько неожиданный результат, состоящий в том, что существуют универсальные программы, то есть программы, которые в некотором смысле реализуют все другие программы. Этот результат является одним из основных результатов теории вычислимости.
Определение 6.1. Универсальной функцией для n -местных вычислимых функцийназывается (n+ 1)-местная функция
 .
.
Для примера рассмотрим функцию 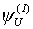 . Эта функция реализует все одноместные вычислимые функции
. Эта функция реализует все одноместные вычислимые функции 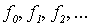 . Действительно, для произвольного неотрицательного целого числа т функция
. Действительно, для произвольного неотрицательного целого числа т функция 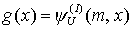 совпадает с функцией
совпадает с функцией 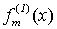 . Таким образом, название функции
. Таким образом, название функции 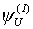 вполне соответствует классу вычисляемых ею одноместных функций.
вполне соответствует классу вычисляемых ею одноместных функций.
Ниже для простоты вместо 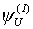 будем писать
будем писать  .
.
Теорема 6.1. Для каждого натурального числа n универсальная функция 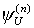 вычислима.
вычислима.
Доказательство. Покажем, как можно вычислить значение функции 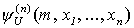 для заданного числа m и фиксированного набора (x1,..., xn). Неформальная процедура вычисления значения
для заданного числа m и фиксированного набора (x1,..., xn). Неформальная процедура вычисления значения 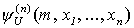 состоит в следующем: "Декодируйте число m и восстановите программу Рm. Затем имитируйте вычисление по этой программе. Если вычисление по программе заканчивается, требуемое значение
состоит в следующем: "Декодируйте число m и восстановите программу Рm. Затем имитируйте вычисление по этой программе. Если вычисление по программе заканчивается, требуемое значение 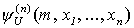 содержится в регистре R1 ". По тезису Черча заключаем, что функция
содержится в регистре R1 ". По тезису Черча заключаем, что функция 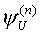 вычислима.
вычислима.
Определение 6.2. Любая программа Р(n), вычисляющая функцию 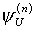 , называется универсальной программой.
, называется универсальной программой.
Универсальные программы полностью соответствуют своему названию. Действительно, так как универсальная программа Р(n) позволяет вычислить любую n- местную вычислимую функцию, то, по сути дела, программа Р(n) заменяет абсолютно все программы для вычисления n- местных функций.
Проиллюстрируем теперь, как использовать вычислимость универсальных функций в диагональных построениях.
7. Алгоритмически неразрешимые проблемы
Основным стимулом, приведшим к выработке понятия алгоритма и созданию теории алгоритмов, явилась потребность доказательства неразрешимости многих проблем, возникших в различных областях математики. Специалист, решая задачу, всегда должен считаться с возможностью того, что она может оказаться неразрешимой.
При доказательстве неразрешимости той или иной проблемы часто используется так называемый метод сводимости, заключающийся в следующем. Пусть, например, в результате некоторых рассуждений удалось показать, что решение проблемы Pr1 приводит к решению другой проблемы Pr2. В этом случае говорят, что проблема Pr2 сводится к проблеме Pr1. Таким образом, если проблема Pr2 сводится к проблеме Pr1, то из разрешимости Pr1 следует разрешимость Pr2 и, наоборот, из неразрешимости Pr2 следует неразрешимость Pr1. В данном разделе метод сводимости используется при доказательстве теоремы 7.3.
Ниже доказывается неразрешимость ряда известных проблем.
Теорема 7.1. Проблема "функция 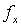 всюду определена" неразрешима.
всюду определена" неразрешима.
Доказательство. Пусть g - характеристическая функция этой проблемы
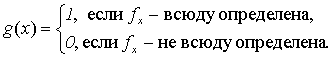
Нам надо показать, что функция g невычислима.
От противного, предположим, что g - вычислимая функция. Рассмотрим функцию

Функция f всюду определена и отличается от каждой вычислимой функции 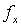 .
.
Применяя g и универсальную функцию  , запишем f в виде:
, запишем f в виде:
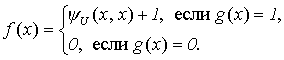
Из вычислимости функций g и  по тезису Черча следует вычислимость функции f.
по тезису Черча следует вычислимость функции f.
Полученное противоречие доказывает невычислимость функции g. Таким образом, проблема "функция 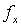 всюду определена" неразрешима.
всюду определена" неразрешима.
Обозначим область определения 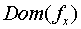 и множество значений
и множество значений 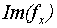 функции
функции 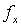 через
через 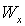 и
и 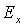 соответственно.
соответственно.
Теорема 7.2. Проблема " 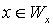 " неразрешима.
" неразрешима.
Доказательство. Характеристическая функция этой проблемы задается следующим образом:
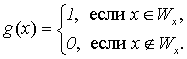
Предположим, что функция g вычислима, и приведем это предположение к противоречию.
Рассмотрим функцию

Так как функция g вычислима, то по тезису Черча функция f также вычислима. С другой стороны, для любого x область определения Dom (f) функции f отлична от области определения 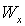 , и, следовательно,
, и, следовательно, 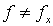 .
.
Таким образом, предположение о вычислимости характеристической функции g неверно. Поэтому проблема " 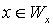 " неразрешима.
" неразрешима.
Замечание 7.1. Доказанная теорема вовсе не утверждает, что мы не можем для любого конкретного числа a сказать, будет ли определено значение 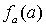 . В теореме лишь утверждается, что не существует единого общего метода решения вопроса о том, будет ли значение
. В теореме лишь утверждается, что не существует единого общего метода решения вопроса о том, будет ли значение  определено.
определено.
Замечание 7.2. Проблему " 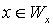 " называют также проблемой самоприменимости. Такое название связано с формулировкой проблемы в форме: "Остановится ли МНР, работая по программе
" называют также проблемой самоприменимости. Такое название связано с формулировкой проблемы в форме: "Остановится ли МНР, работая по программе 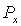 с начальной конфигурацией (x)?". Другими словами: "Применима ли программа к своему кодовому номеру?".
с начальной конфигурацией (x)?". Другими словами: "Применима ли программа к своему кодовому номеру?".
Теорема 7.3. Проблема "  " неразрешима.
" неразрешима.
Доказательство. Если бы проблема "  " была разрешима, то была бы разрешима более простая проблема "
" была разрешима, то была бы разрешима более простая проблема " 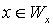 ", что противоречит доказанной выше теореме.
", что противоречит доказанной выше теореме.
Замечание 7.3. Доказанную теорему часто интерпретируют как утверждение о неразрешимости проблемы остановки, в которой говорится, что не существует общего метода, устанавливающего, остановится ли некоторая конкретная программа, запущенная с некоторым конкретным набором начальных данных.
Смысл этого утверждения для теоретического программирования очевиден: не существует общего метода проверки программ на наличие в них бесконечных циклов.
В доказательстве теоремы мы показали, что проблема остановки "  ", по крайней мере, не проще, чем проблема самоприменимости "
", по крайней мере, не проще, чем проблема самоприменимости " 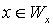 ". Мы свели вопрос о неразрешимости одной проблемы к другой. Это прием часто используется при доказательстве неразрешимости проблем.
". Мы свели вопрос о неразрешимости одной проблемы к другой. Это прием часто используется при доказательстве неразрешимости проблем.
8. s-m-n-теорема
В этом разделе мы докажем теорему, принадлежащую к числу основных результатов теории алгоритмов. Суть теоремы в следующем. Допустим, что f (х, у) - вычислимая функция. Для каждого фиксированного значения a переменной х функция f порождает одноместную вычислимую функцию ga (y) = f (a, у). Из вычислимости функции ga следует существование индекса b такого, что f (a, у) = fb (у). Оказывается индекс b можно эффективно вычислить по параметру а.
Теорема 8.1 (s-m-n - теорема, простая форма). Пусть f (х, у) -вычислимая функция. Существует всюду определенная вычислимая функция s (x), такая, что f (х, у) = fs(x) (у).
Доказательство. Из вычислимости функции f (х, у) следует существование МНР-программы Pr, которая, исходя из начальной конфигурации (x, y, 0, 0,...), вычисляет значение функции f от двух аргументов х и у. Изменим программу Pr, добавив спереди команды, преобразующие начальную конфигурацию
| R1 | R2 | R3 | R4 | ... | ||
| y | 0 | 0 | 0 | ... | (*) |
в конфигурацию
| R1 | R2 | R3 | R4 | ... | |
| a | y | 0 | 0 | ... |
следующим образом:
T (1, 2)
Z (1)
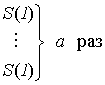
Pr
Новая программа Pr1, примененная к начальной конфигурации (*), вычисляет значение функции ga (y) = f (a, у) от одного аргумента у.
Теперь рассмотрим функцию s (a) = (Pr1), сопоставляющую произвольному неотрицательному целому числу a геделев номер программы Pr1. Функция s всюду определена и по тезису Черча вычислима. Кроме того, по построению fs(a) (у) = f (a, у) для каждого 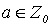 .
.
Замечание 8.1. Сформулированную теорему называют также теоремой параметризации, поскольку она позволяет по заданной вычислимой функции f (x, у) и фиксированному параметру a найти геделев номер s (a) программы, вычисляющей функцию fs(a) (у) = f (a, у).
Доказанная выше теорема 8.1 является частным случаем более общей теоремы.
Теорема 8.2 (s-m-n - теорема). Пусть m, n - натуральные числа, 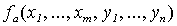 - вычислимая функция с геделевым номером a. Существует всюду определенная вычислимая функция
- вычислимая функция с геделевым номером a. Существует всюду определенная вычислимая функция  такая, что
такая, что
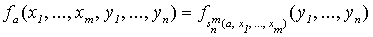 .
.
Доказательство сформулированного утверждения аналогично доказательству теоремы 8.1.
Замечание 8.2. Название теоремы 8.2 связано с обозначением  для функций в формулировке теоремы.
для функций в формулировке теоремы.
Покажем теперь, как можно использовать s-m-n -теорему для доказательства неразрешимости проблем. s-m-n -теорема часто используется для сведения проблемы " 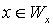 " к другим проблемам.
" к другим проблемам.
Теорема 8.3. Проблема "  " неразрешима.
" неразрешима.
Доказательство. Рассмотрим функцию

По тезису Черча функция f (x, y) вычислима. Отсюда по s-m-n-теореме вытекает существование всюду определенной вычислимой функции s(x) такой, что  . По определению функции f (x, y) имеем:
. По определению функции f (x, y) имеем:
 .
.
Следовательно, истинность условия 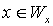 можно установить, определив справедливость равенства
можно установить, определив справедливость равенства 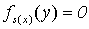 . Тем самым мы свели проблему "
. Тем самым мы свели проблему " 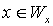 " к проблеме "
" к проблеме "  ". Поскольку первая из них неразрешима, то неразрешима и вторая.
". Поскольку первая из них неразрешима, то неразрешима и вторая.
Замечание 8.3. Теорема 8.3 показывает, что в области проверки правильности компьютерных программ имеются принципиальные ограничения. В ней говорится о том, что не существует алгоритма проверки того, будет ли программа вычислять нулевую функцию. Несколько изменив доказательство теоремы 8.3, можно убедиться в том, что то же самое справедливо и для любой другой конкретной вычислимой функции.
Теорема 8.4. Проблема  неразрешима.
неразрешима.
Доказательство. Допустим, что проблема  разрешима. Тогда разрешима и проблема
разрешима. Тогда разрешима и проблема 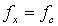 , где c - индекс функции 0
, где c - индекс функции 0 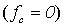 . Однако, это противоречит теореме 8.3. Таким образом, проблема
. Однако, это противоречит теореме 8.3. Таким образом, проблема  неразрешима.
неразрешима.
Замечание 8.4. Из теоремы 8.4 следует, что вопрос о том, вычисляют ли две программы одну и ту же одноместную функцию, неразрешим. Важность этого результата для теоретического программирования очевидна.
Упражнения
8.1. Докажите, что не существует алгоритма, определяющего по тексту программы, будет ли эта программа вычислять некоторую конкретную вычислимую функцию.
8.2. 2. Покажите, что не существует всюду определенной вычислимой функции f (x, y), обладающей следующим свойством: если программа 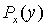 останавливается, то это происходит за f (x, y)или меньше шагов.
останавливается, то это происходит за f (x, y)или меньше шагов.
Указание. Покажите, что если бы такая функция существовала, то проблема остановки была бы разрешима.
Естественно задаться вопросом, какие свойства вычислимых функций можно алгоритмически распознать по их программам. Оказывается, что никакие, кроме тривиальных. Доказательство этого факта содержится в теореме Райса.
Теорема 8.5 (теорема Райса). Пусть B - непустое множество одноместных вычислимых функций, не совпадающее со всем множеством 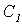 одноместных вычислимых функций. Тогда проблема "
одноместных вычислимых функций. Тогда проблема " 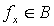 " неразрешима.
" неразрешима.
Доказательство. Очевидно, что проблема " 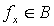 " разрешима тогда и только тогда, когда разрешима проблема "
" разрешима тогда и только тогда, когда разрешима проблема "  ". Поэтому без потери общности можно считать, что нигде не определенная функция
". Поэтому без потери общности можно считать, что нигде не определенная функция 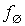 не принадлежит B.
не принадлежит B.
Выберем некоторую функцию 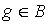 и рассмотримфункцию
и рассмотримфункцию

По тезису Черча функция f (x, y) вычислима. Поэтому существует (по s-m-n-теореме) всюду определенная вычислимая функция s(x) такая, что  . По определению функции f (x, y) имеем:
. По определению функции f (x, y) имеем:
 .
.
Таким образом, с помощью вычислимой функции s (x) мы свели проблему " 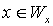 " к проблеме "
" к проблеме " 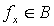 ". Следовательно, проблема "
". Следовательно, проблема " 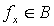 " неразрешима.
" неразрешима.
Дадим более содержательную формулировку теоремы Райса. Пусть Q некоторое свойство одноместных вычислимых функций. Свойство Q назовем нетривиальным, если существуют функции, обладающие свойством Q, и функции не обладающие этим свойством.
Все обычно рассматриваемые свойства являются нетривиальными. Примерами нетривиальных свойств служат следующие:
- функция тождественно равна нулю;
- функция нигде не определена;
- функция всюду определена;
- функция взаимно однозначна;
- функция определена при x = 0.
Так как вычислимые функции могут быть заданы программами их вычисления, то естественно возникает вопрос: можно ли по программе узнать, обладает ли соответствующая ей функция заданным нетривиальным свойством.
Теорема 8.6. Каково бы ни было нетривиальное свойство Q одноместных вычислимых функций, задача распознавания этого свойства алгоритмически неразрешима.
Доказательство. Пусть B - множество одноместных вычислимых функций, обладающих свойством Q. Множество B не пусто и не совпадает со всем множеством одноместных вычислимых функций. По теореме Райса проблема " 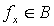 " неразрешима.
" неразрешима.
Из последней теоремы следует неразрешимость многих задач, связанных с программированием. Например, если имеется некоторая программа, то по ней, вообще говоря, ничего нельзя сказать о функции, реализуемой программой. По двум программам нельзя установить, реализуют ли они одну и ту же функцию, а это приводит к неразрешимости многих задач, связанных с эквивалентными преобразованиями и минимизацией программ. В любом алгоритмическом языке, какие бы правила синтаксиса там ни применялись, всегда будут иметься "бессмысленные" программы, задающие функции не определенные ни в одной из точек (эти программы нельзя обнаружить). Теорема Райса позволяет доказывать алгоритмическую неразрешимость многих задач, связанных с вычислениями на компьютерах.
Более подробно ознакомиться с формальными подходами к вычислимости можно по книгам [4, 5].
ЛИТЕРАТУРА
1. Основы информатики и вычислительной техники. Пробное учебное пособие для средних учебных заведений. Ч. 1. Под ред. А. П. Ершова и В. М. Монахова. - М: Просвещение, 1985.
2. Ершов А. П. Алгоритмический язык. - Наука и жизнь. - 1985. - №11. - С. 61-63.
3. Абрамов С. А. Математические построения и программирование. - М.: Наука, 1978.
4. Катленд Н. Вычислимость. Введение в теорию рекурсивных функций. - М.: Мир, 1983.
5. Трахтенброт В. Л. Алгоритмы и вычислительные автоматы. - М.: Советское радио, 1974.