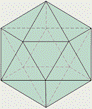
тетраэдр куб октаэдр додекаэдр икосаэдр
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
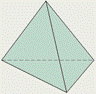
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.
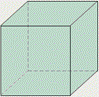
У куба (правильный гексаэдр) все грани – квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами.
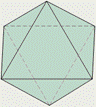
У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.
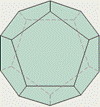
У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.
У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.
Тема 3.3. Тела и поверхности вращения
Цилиндр
Цилиндрическая поверхность – поверхность, образуемая движением прямой (в каждом своём положении называемой образующей) вдоль кривой (называемой направляющей) так, что прямая постоянно остаётся параллельной своему начальному положению.
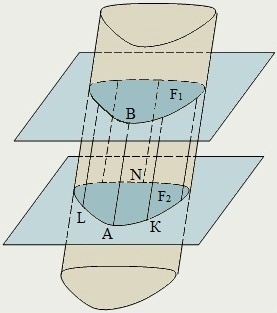Прямая АВ – образующая;
кривая AKNLA – направляющая.
Бесконечный цилиндр – тело, ограниченное цилиндрической поверхностью.
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называется боковой поверхностью цилиндра.
Высотой цилиндра называется расстояние между плоскостями его оснований.
Другая часть, ограниченная параллельными плоскостями – это основания цилиндра.
Отрезок АВ – образующая;
фигуры F1 и F2 – основания.
У цилиндра:
· основания равны;
· образующие параллельны и равны.
Боковая поверхность всякого цилиндра равна произведению образующей на периметр перпендикулярного сечения.
Объём всякого цилиндра равен произведению площади основания на высоту:
V = SH.
Цилиндр, у которого основания перпендикулярны образующим и являются кругами, называется прямым круговым цилиндром (часто, и далее, – просто цилиндром).
Прямой круговой цилиндр можно получить вращением прямоугольника вокруг одной из его сторон.
Радиусом цилиндра называется радиус его основания.
Осью цилиндра называется прямая, проходящая через центры его оснований. Ось цилиндра параллельна образующим.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевым сечением цилиндра (прямого кругового цилиндра) является прямоугольник.
AO1 – радиус цилиндра;
AB, CD – образующие цилиндра;
O1O2 – ось цилиндра;
AB, CD, O1O2 – высоты цилиндра;
ABCD – осевое сечение цилиндра.
Боковая поверхность прямого кругового цилиндра равна произведению длины окружности основания на высоту:
Sбок = 2πRH.
Полная поверхность цилиндра вычисляется по формуле:
Sп = Sбок + 2Sосн = 2πR(H + R).
Для объёма прямого кругового цилиндра верно:
V = πR2H.
Конус
Конической поверхностью называется поверхность, образуемая движением прямой, проходящей всё время через неподвижную точку вдоль данной линии.
Эта линия называется направляющей, двигающаяся прямая, в каждом своём положении, – образующей, а неподвижная точка – вершиной.
Конусом называется тело, ограниченное одной полостью конической поверхности с замкнутой направляющей и плоскостью, пересекающей все образующие этой полости и не проходящей через вершину.
Часть этой плоскости, лежащая внутри конической поверхности, называется основанием конуса.
Высота конуса – это перпендикуляр, опущенный из вершины конуса на плоскость основания.
Часть конической поверхности, расположенная между вершиной и плоскостью основания, называется боковой поверхностью конуса.
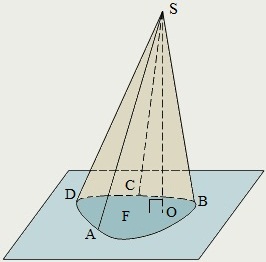
Кривая ABCDA – направляющая;
прямая SА – образующая;
точка S – вершина;
отрезок SО – высота;
фигура F – основание конуса.
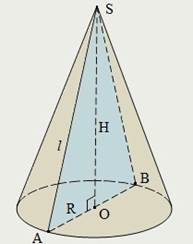Конус называется прямым круговым, если его направляющая – окружность, а вершина ортогонально проектируется в его центр.
В элементарной геометрии прямой круговой конус часто называют просто конусом.
Прямой круговой конус можно получить вращением прямоугольного треугольника вокруг одного из его катетов. При этом вращении другой катет опишет основание конуса, а гипотенуза – боковую поверхность.
Осью прямого кругового конуса называется прямая, содержащая его высоту.
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса.
Боковая поверхность прямого кругового конуса равна произведению половины длины окружности основания на образующую:
Sбок = πR l.
Полная поверхность прямого кругового конуса вычисляется по формуле:
Sп = Sбок + Sосн= πR(l + R).
Для объёма прямого кругового конуса верно:
V = (πR2H)/3.
Шар
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не больше данного, от данной точки. Эта точка называется центром шара (на рисунке – это точка О), а данное расстояние (на рисунке – R) – радиусом шара.
Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси.
Граница шара называется шаровой поверхностью или сферой. Таким образом, точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок (ОА), соединяющий центр шара с точкой шаровой поверхности, также называется радиусом.
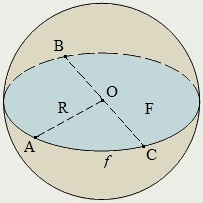Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром (ВС). Концы любого диаметра называются диаметрально противоположными точками шара (точки В и С).
Сечение шара плоскостью, проходящей через его центр, называется большим кругом (фигура F), а сечение сферы – большой окружностью (линия f на рисунке).
Любая плоскость, проходящая через центр шара, является его плоскостью симметрии. Центр шара является его центром симметрии.
Площадь сферы и объём шара можно найти по формулам:
S = 4πR2= πD2;
V = (4πR3)/3 = (πD3)/6,
где R – радиус, D – диаметр сферы и шара.