Я́коб Берну́лли (27 декабря1654, Базель, – 16 августа1705, там же) –швейцарский математик, профессор математики Базельского университета (с 1687 года). Один из основателей теории вероятностей и математического анализа.
Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p.
Примем число появлений события в каждом из испытаний за некоторую случайную величину Х.
Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.
Значения найти достаточно просто. Очевидно, что в результате п испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. до п раз.
Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли. 
Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.
Распределение Пуассона
Распределение Пуассона представляет собой предельный случай биномиального, когда вероятность р очень мала, а число испытаний n велико.
Таким образом, им можно пользоваться при описании частот распределения редких событий, таких, например, как случай обширных наводнений на протяжении долгого периода времени наблюдений.
Дискретная случайная величина Х, которая может принимать только целые неотрицательные значения с вероятностями
, (1)
где k – число появления событий в n независимых испытаниях, l = n · p (среднее число появлений события в n испытаниях), называется распределенной по закону Пуассона с параметром l.
|
|
В отличие от биномиального распределения здесь случайная величина может принимать бесконечное множество значений, представляющее собой бесконечную последовательность целых чисел 0, 1, 2, 3, ….
Закон Пуассона описывает число событий k, происходящих за одинаковые промежутки времени. При этом полагается, что события появляются независимо друг от друга с постоянной средней интенсивностью, которая характеризуется параметром l = n · p. Так как для распределения Пуассона вероятность р появления события в каждом испытании мала, то это распределение называют законом распределения редких явлений.
По распределению Пуассона распределено, например число посетителей магазина или банка за определенный промежуток времени, при этом l – среднее число посетителей за это время.
Пример. Предположим, что в среднем в магазин приходит 2,1 покупатель в минуту. Тогда, используя (1), получаем, например, вероятности того, что магазин посетят за минуту 1, 4 и 10 посетителей:
, 
, 
.
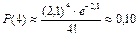Основанием считать статистическое распределение пуассоновским является близость значений статистических характеристик 
и S 2 (которые являются статистическими приближениями математического ожидания и дисперсии), так как для теоретического распределения Пуассона имеет место: М (Х) = D (X) = l.