Модель Моно
При непрерывном перемешивании можно считать весь объем культиватора однородно заполненным, концентрации субстрата и клеток в каждой точке культиватора одинаковыми, и описывать поведение этих концентраций во времени с помощью системы обыкновенных дифференциальных уравнений:
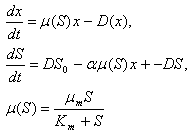(11.8)
Здесь S - концентрация субстрата
x - концентрация клеток в культиваторе
S 0 -концентрация субстрата, поступившего в культиватор
D - скорость протока (разбавления) культуры
a - 1 - “экономический коэффициент, показывающий, какая часть поглощенного субстрата идет на приращение биомассы.
Поясним смысл членов, входящих в правые части уравнений. В первом уравнении: m(S)x ‑ прирост биомассы за счет поглощения субстрата, ‑ Dx - отток биомассы из культиватора.
Во втором уравнении:‑ am(S)x ‑ количество субстрата, поглощенного клетками культуры, DS 0 ‑ приток субстрата в культиватор, ‑DS ‑ отток неиспользованного субстрата из культиватора.
Скорость роста биомассы предполагается зависящей только от концентрации субстрата в соответствии с формулой Моно (третье уравнение).
Исследуем тип стационарных режимов и переходных процессов в культиваторе, используя методы, изученные в лекциях (3-5).
Введем безразмерные концентрации, время и скорость протока
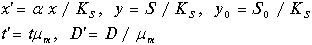
Штрихи у новых переменных опустим. В новых переменных система имеет вид:
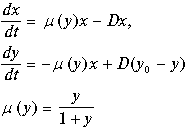(11.9)
Найдем стационарные концентрации биомассы и субстрата. Приравняем правые части уравнений нулю
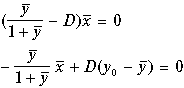(11.10)
Система алгебраических уравнений (11.10) имеет два решения, следовательно, система дифференциальных уравнений (11.9) имеет два стационарных состояния
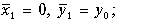(11.11)
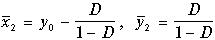(11.12)
Примем во внимание, что безразмерная концентрация клеток x имеет смысл только при значениях x> 0, а безразмерная концентрация субстрата y ограничена сверху значением y 0 =S 0 /K ‑ концентрацией притекающего субстрата. Легко видеть, что ненулевое стационарное значение биомассы (11.12) имеет смысл только в случае, когда безразмерная скорость протока D меньше определенной величины
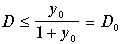(11.13)
Граничное значение скорости протока называется скоростью вымывания. В размерном виде его величина равна:
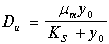(11.14)
При скоростях протока, больших Dв, прирост биомассы не может компенсировать ее отток, и культура полностью вымывается из культиватора.
Определим характер устойчивости стационарных состояний системы, используя метод линеаризации системы в окрестности стационарного состояния, рассмотренный в лекции 4.
Характеристический определитель системы (11.9) имеет вид.
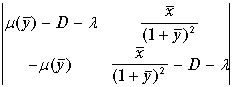. (11.15)
Исследуем характер устойчивости режима вымывания ‑ особой точки с координатами (11.11). В этом случае
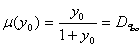. (11.16)
и характеристический определитель принимает вид
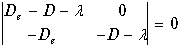(11.17)
Корни характеристического уравнения (11.17)
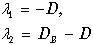(11.18)
действительны и имеют различные знаки при D<DВ, то есть при скоростях разбавления, меньших скоростей вымывания. При этом точка (0 ,y 0 ) неустойчива ‑ седло.
Если же D>DВ ‑ оба корня отрицательны, и особая точка (11.11) является устойчивым узлом. Этот режим называется режимом вымывания.
Концентрация субстрата в культиваторе равна при этом концентрации поступающего субстрата S 0, а концентрация биомассы равна нулю. Если в такой культиватор заложить “затравку”, мироорганизмы будут вымыты из культиватора, не успев размножиться.
Для второй особой точки с координатами (11.12) корни характеристического уравнения равны
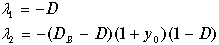
(11.19)
Напомним, что это ненулевое по биомассе состояние равновесия существует в положительном квадранте фазовой плоскости лишь при значениях скорости разбавления D<DВ. Так как
,
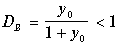то все три сомножителя, входящие в выражение для l 2 в (11.19) положительны. Следовательно, l 2<0, и точка (11.12) ‑ устойчивый узел. Это и есть рабочее состояние проточного культиватора.
Фазовые портреты системы для двух значений скоростей протока D<DВ и D>DВ приведены на рис.11.4 (а, б)
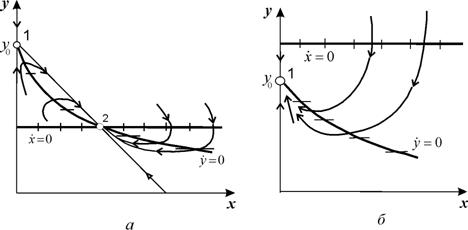
Рис. 11.4. Фазовые портреты системы 11.9.
а – стационарный режим работы, б – режим вымывания.
Пояснения в тексте
Уравнение изоклины горизонтальных касательных получим, приравняв правую часть второго уравнения (11.9) нулю
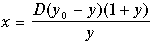(9.20)
Изоклины вертикальных касательных на рисунках 11.4: ось x= 0 и прямая
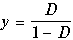(11.21)
В случае, когда D<DВ главные изоклины (11.20) и (11.21) пересекаются в положительном квадранте, и точка их пересечения является устойчивым узлом, а точка пересечения кривой (9.20) с осью x = 0 – седлом (рис.11.4 а)
В случае D>DВ главные изоклины (11.20) и (11.21) пересекаются вне положительного квадранта, и устойчивым узлом будет особая точка (11.11), соответствующая режиму вымывания (рис.11.4 б).
Рассмотренная модель является упрощенной и для описания реальных процессов требует дополнений. Например, при больших концентрациях субстрат может оказывать ингибирующее действие, и тогда формулу для скорости роста следует записывать в виде:
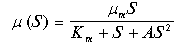(11.22)
В системе, где существует такая зависимость скорости роста от субстрата, возможны триггерные режимы - наличие двух устойчивых стационарных состояний и зависимость стационарных значений концентраций субстрата и биомассы от начальных условий (от величины затравки и начальной концентрации биомассы).
На скорость роста биомассы может оказывать влияние концентрация продуктов метаболизма в среде, окружающей клетку. Тогда к двум уравнениям, описывающим динамику концентрации биомассы и субстрата в непрерывном процессе культивирования, следует добавить третье уравнение, выражающее динамику концентрации продуктов метаболизма. При этом скорость роста биомассы будет зависеть как от концентрации субстрата. Так и от концентрации продукта. Наиболее известную формулу такой зависимости предложил Иерусалимский:
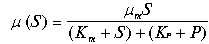(11.23)
Формула (11.23) известна как формула Моно-Иерусалимского.
Исследование модели, учитывающей ингибирующее действие продукта показывает, что значение скорости вымывания в такой системе совпадает с величиной DВ, полученной выше для модели Моно. В то же время ингибирующее влияние продукта ведет к значительному уменьшению стационарных концентраций биомассы.
Микроэволюционные процессы в микробных популяциях
Быстрота смены поколений делает микробные популяции чрезвычайно удобным объектом для изучения процессов микроэволюции. Пусть требуется изучить микроэволюционный процесс в популяции, протекающий в течение 100 генераций, например, проследить последствия повышения фона радиации. В популяции однолетних организмов (например, сельскохозяйственных культур) для проведения такого исследования не хватит всей жизни одного исследователя. Для человеческой популяции на сто поколений приходится период времени более 2000 лет. А для микробной популяции с временем генерации g =20 мин. наблюдение 100 генераций займет около полутора суток.
Рассмотрим процесс восстановления популяции после воздействия неблагоприятного фактора. Пусть процесс происходит в условиях непрерывного культивирования. Предположим, что в микробной популяции в результате воздействия неблагоприятного внешнего воздействия погибает значительная часть клеток. После снятия неблагоприятного фактора в популяции будет происходить процесс восстановления. В результате действия протока количество мертвых клеток будет уменьшаться, а количество живых будет определяться двумя процессами ‑ вымыванием и размножением. Со временем доля живых клеток увеличивается, и популяция возвращается к активному состоянию.
Рассмотрим простейшую модель такой системы (Н.С.Печуркин). Разделим все клетки на два типа. Первый тип ‑ потерявшие способность к размножению в результате воздействия неблагоприятного фактора неживые клетки. Второй тип ‑ сохранившие способность к размножению клетки. Динамика живых и неживых клеток может быть описана системой уравнений.
(11.24)
Здесь xж ‑ концентрация живых клеток,
xн -‑ концентрация неживых клеток
x ‑ общая концентрация клеток в популяции
S ‑ концентрация лимитирующего субстрата.
Функция m(S), характеризующая зависимость скорости роста живых клеток от концентрации лимитирующего субстрата может быть представлена в форме Моно, или в виде более сложной функции.
Если воздействие неблагоприятного фактора было сильным, и погибла значительная часть популяции, потребление субстрата в начальные моменты процесса восстановления будет незначительным. Концентрация субстрата в среде значительно повысится за счет его постоянного поступления. При этом можно считать, что m=mmax=const.
Тогда уравнение для субстрата можно исключить из рассмотрения. Анализ кинетики восстановления сведется к рассмотрению простой системы первых двух уравнений и алгебраического соотношения для количества клеток. Решив систему уравнений, получим соотношение, определяющее долю живых клеток в популяции в любой момент времени t
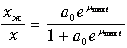(11.25)
где a 0‑ отношение количества живых и неживых клеток в начальный момент времени.
Можно оценить время, которое необходимо популяции для устранения последствий неблагоприятного фактора. Будем считать процесс восстановления законченным, если в популяции на сто живых осталась одна неживая клетка. Пусть в результате неблагоприятного воздействия в популяции отношение живых клеток к неживым составляло 1:100. Оценки (Печуркин, 1978) показывают, что для изменения соотношения числа живых и неживых клеток в 104 раз необходимо примерно тринадцать с половиной поколений культуры. Даже при очень сильном неблагоприятном воздействии, например при a 0 = 10 -7, время восстановления до 90% уровня живых клеток составляет 27 генераций. Это объясняется логарифмической зависимостью времени восстановления от отношения живых и неживых клеток.
На сходных моделях можно анализировать конкуренцию мутантных форм в микробных культурах. Несмотря на то, что частота мутаций, приводящих к улучшению некоторого признака чрезвычайно низка, именно такие мутанты вытесняют исходную форму за счет действия естественного отбора. Анализ экспериментального материала на основе таких моделей позволил сделать определенные выводы о совместном действии мутаций и отбора. А именно, преимущества имеют следующие мутанты.
· Мутанты, способные более полно утилизировать имеющийся субстрат, то есть имеющие отличную от исходной форму зависимость m=f(S ).
· “Экономичные” мутанты, способные более полно использовать субстрат.
· Более “резистентные” мутанты, менее чувствительные к воздействию внешнего фактора.
· Мутанты с пониженными скоростями отмирания.
· Менее “мутабельные” мутанты.
· Быстро растущие и быстро отмирающие мутанты
· Мутанты с увеличенной максимальной скоростью роста
· Мутанты, выделяющиеся в неоднородных средах, например, способные противостоять вымыванию из ферментера: прилипать к стенкам или слипаться в комки и выпадать на дно.
· Оценка времени замены исходной формы мутантной при воздействии неблагоприятного фактора (например, антибиотика), показывает, как быстро распространяются нечувствительные к ингибиторам мутанты в открытых системах.