Занятие 1. Комбинаторика.
Основные комбинаторные правила
Правило суммы
Если множество 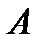 содержит
содержит  элементов, а множество
элементов, а множество  –
–  элементов и пересечение множеств
элементов и пересечение множеств  и
и  пусто,
пусто, 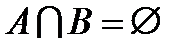 , то число элементов в их объединении
, то число элементов в их объединении 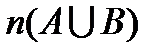 равно сумме элементов множеств
равно сумме элементов множеств  и
и  :
: 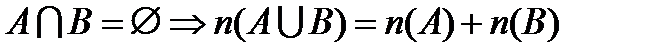 .
.
Число элементов  во множестве
во множестве  называется его мощностью.
называется его мощностью.
Пример 1. Сколько существует способов поставить белопольного слона на шахматную доску, чтобы он держал под боем больше 10 полей.
| Рис. 1 |
Теорема. Если множество
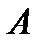 содержит
содержит  элементов, а множество
элементов, а множество 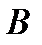 –
–  элементов и пересечение множеств
элементов и пересечение множеств  и
и  не пусто,
не пусто,  , то число элементов в их объединении
, то число элементов в их объединении  вычисляется по формуле:
вычисляется по формуле: 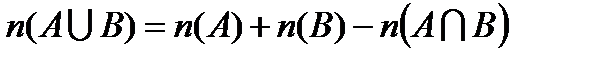 .
.
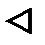 Доказательство. Множество
Доказательство. Множество 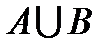 и множество
и множество 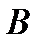 можно представить как объединение двух непересекающихся множеств:
можно представить как объединение двух непересекающихся множеств: 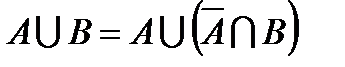 ,
, 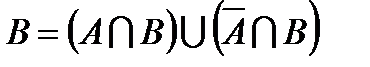 . Тогда по правилу суммы имеем:
. Тогда по правилу суммы имеем:
 (1)
(1)
 . (2)
. (2)
Вычитая из выражения (1) выражение (2), получаем: 

 .
.
Окончательно имеем: 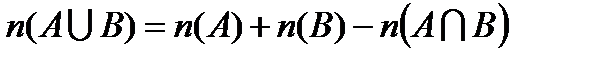 , что и требовалось доказать.
, что и требовалось доказать. 
Методом математической индукции формулу можно обобщить на сумму любого конечного числа множеств. В частности для трех конечных множеств имеем.
Следствие.

 (3)
(3)
Пример 2. В школе работают кружки: математический, английского языка и спортивный. В математическом кружке занимается 150 учеников, в кружке английского языка - 80 учеников, в спортивном - 110 учеников. В кружках английского языка и спортивном занимаются 60 учеников, в математическом и спортивном - 70 учеников, в кружках математическом и английском - 40 учеников. Во всех трех кружках занимается 21 ученик. Ни один кружок не посещает 14 учеников. Найти число учащихся в школе.
Введем следующие обозначения:
 - множество учеников школы - основное множество;
- множество учеников школы - основное множество;
 - множество учеников, посещающих кружок английского языка;
- множество учеников, посещающих кружок английского языка;
 - множество учеников, состоящих в математическом кружке;
- множество учеников, состоящих в математическом кружке;
 - множество учеников, занимающихся в спортивном кружке
- множество учеников, занимающихся в спортивном кружке
 - число учеников, не занимающихся ни в одном кружке.
- число учеников, не занимающихся ни в одном кружке.
По условию 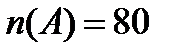 ,
, 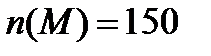 ,
,  ,
, 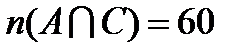 ,
,  ,
,  ,
,  ,
, 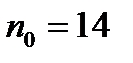 .
.
Тогда число учеников в школе  можно вычислить по формуле (3).
можно вычислить по формуле (3). 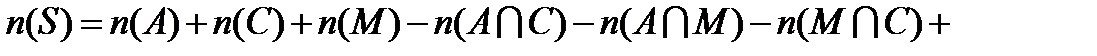
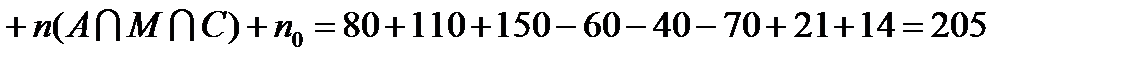 .
.
Правило произведения
Пусть заданы два конечных множества 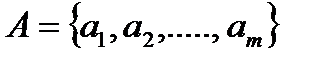 и
и  . Тогда множество всех возможных упорядоченных пар в их декартовом произведении
. Тогда множество всех возможных упорядоченных пар в их декартовом произведении 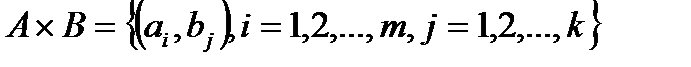 равно произведению чисел элементов в каждом из этих множеств:
равно произведению чисел элементов в каждом из этих множеств:  .
.
Пример 3. В урне лежат пять белых шаров, перенумерованных цифрами 1, 2, 3, 4, 5, три красных шара перенумерованных цифрами 1, 2, 3 и два синих шара перенумерованных цифрами 1, 2. Сколько можно составить разноцветных упорядоченных "троек" из этих шаров?
Обозначим множество белых шаров буквой 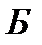 с элементами
с элементами  , множество красных шаров
, множество красных шаров 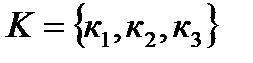 и множество синих шаров
и множество синих шаров  . Тогда по правилу произведения число разноцветных упорядоченных троек вычисляется по формуле:
. Тогда по правилу произведения число разноцветных упорядоченных троек вычисляется по формуле:  .
.
Пример 4. Сколько четырехзначных четных чисел можно составить из семи цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться.
Согласно правилу произведения имеется 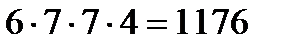 способов составить четырехзначное четное число из данных семи цифр.
способов составить четырехзначное четное число из данных семи цифр.
Пример 5. Сколько можно образовать различных комбинаций, состоящих из одной буквы и трех цифр, если использовать 32 буквы и 10 цифр? Известно, что в комбинации цифры не могут повторяться, а нуль не может стоять на первом месте (в старшем разряде комбинации).
Обозначим множество букв -  , а множество цифр -
, а множество цифр -  . В каждой комбинации на первом месте может стоять либо цифра, либо буква. Поэтому рассмотрим два случая.
. В каждой комбинации на первом месте может стоять либо цифра, либо буква. Поэтому рассмотрим два случая.
1. Если на первом месте стоит любая цифра из множества 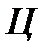 , кроме 0, то имеем три декартовых произведения вида:
, кроме 0, то имеем три декартовых произведения вида:
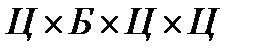
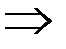 имеем
имеем  возможностей.
возможностей.
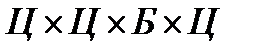
 имеем
имеем  возможностей.
возможностей.
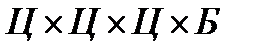
 имеем
имеем  возможностей.
возможностей.
По правилу суммы имеем  различных комбинаций.
различных комбинаций.
2. Если на первом месте стоит буква, то получим декартово произведение вида:  . Число интересующих нас комбинаций равно
. Число интересующих нас комбинаций равно  .
.
Общее число комбинаций, таким образом, составит  .
.
Основные комбинаторные схемы
1. Перестановки. Пусть 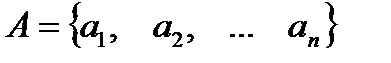 - некоторое конечное множество, состоящее из
- некоторое конечное множество, состоящее из  различных элементов. Соединения, каждое из которых содержит
различных элементов. Соединения, каждое из которых содержит  различных элементов, взятых в определенном порядке, называются перестановками из
различных элементов, взятых в определенном порядке, называются перестановками из 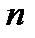 элементов.
элементов.
Число всевозможных перестановок из  элементов равно произведению последовательных натуральных чисел от 1 до
элементов равно произведению последовательных натуральных чисел от 1 до  включительно.
включительно.
 (4)
(4)
Пример 6. Выпишем все перестановки из элементов  . Их будет всего 6:
. Их будет всего 6: 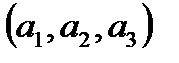 ,
, 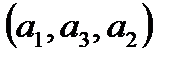 ,
,  ,
,  ,
,  ,
, 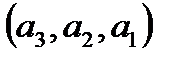 .
.
То же самое число перестановок получим и по формуле (4):  .
.
Пример 7. Сколькими способами пять человек могут сесть на пять стульев?
Ответ.  способов..
способов..
Пример 8. Сколько всего шестизначных четных чисел можно составить из цифр 0, 1, 2, 3, 5, 7, если в каждом из этих чисел ни одна цифра не повторяется?
Решение. Цифрами единиц (младший разряд шестизначного числа) могут быть только 0 или 2. Рассмотрим два случая.
1 случай. Если в младшем разряде стоит 0, то остальные 5 цифр можно разместить на оставшихся 5 местах в любом порядке. А это есть число перестановок из пяти элементов 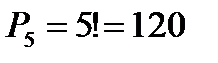 .
.
2 случай. Если в младшем разряде шестизначного числа стоит цифра 2, то в старшем разряде этого числа не может стоять цифра 0, и, следовательно, для цифры старшего разряда имеется 4 возможности. Если на это место поставить одну из цифр 1, 3, 5, 7, то на незанятых 4-х местах может стоять любая из оставшихся 4 цифр, включая 0. Для этого существует  способа. Таким образом, в случае 2 по правилу произведения имеем всего
способа. Таким образом, в случае 2 по правилу произведения имеем всего  способов. Итого по правилу суммы число искомых шестизначных чисел составит
способов. Итого по правилу суммы число искомых шестизначных чисел составит 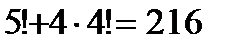 способов.
способов.
Пример 9. Сколькими способами можно рассадить на десяти стульях пять юношей и пять девушек так, чтобы они чередовались?
Решение. Пять девушек, чередуясь, могут выбрать нечетные 5 стульев  способами, оставшиеся 5 четных стульев 5 юношей могут выбрать также
способами, оставшиеся 5 четных стульев 5 юношей могут выбрать также  способами. Всего получаем
способами. Всего получаем  способов. Такое же число способов будет, если девушки займут четные стулья, а юноши нечетные. Окончательно имеем те же самые
способов. Такое же число способов будет, если девушки займут четные стулья, а юноши нечетные. Окончательно имеем те же самые 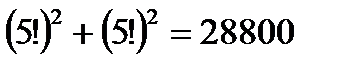
Пример 10. Сколькими способами можно поставить на книжную полку  книг так, чтобы
книг так, чтобы 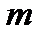 определенных книг стояли рядом?
определенных книг стояли рядом?
Решение. Воспользуемся следующей схемой. Пусть на полке книги стоят так, что первые  мест занимают те самые
мест занимают те самые 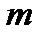 определенных книг.
определенных книг.
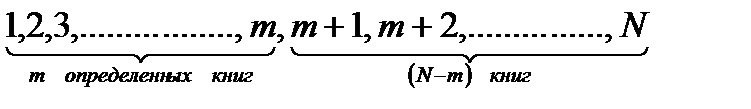
Тогда для этих 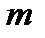 книг имеется
книг имеется 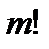 возможных способов расположения (перестановок), а для оставшихся
возможных способов расположения (перестановок), а для оставшихся  книг -
книг -  способов. По правилу произведения всего будет
способов. По правилу произведения всего будет 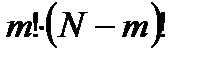 способов расположения.
способов расположения.
Кроме того, в любом из этих способов расстановки первые  книг можно перемещать как единое целое вдоль полки, что можно осуществить
книг можно перемещать как единое целое вдоль полки, что можно осуществить  способами.
способами.
По тому же правилу произведения имеем окончательно  возможностей, удовлетворяющих условию задачи.
возможностей, удовлетворяющих условию задачи.
Пример 11. Сколькими способами можно расставить на шахматной доске размера  восемь разноцветных фишек так, чтобы на каждой горизонтали и на каждой вертикали стояла ровно одна фишка? Ответ:
восемь разноцветных фишек так, чтобы на каждой горизонтали и на каждой вертикали стояла ровно одна фишка? Ответ:  .
.
2. Размещения. Множество вместе с заданным на нем порядком следования называется упорядоченным множеством. Пусть 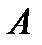 - некоторое конечное множество, состоящее из
- некоторое конечное множество, состоящее из  различных элементов. Составим из элементов этого множества всевозможные неупорядоченные подмножества из
различных элементов. Составим из элементов этого множества всевозможные неупорядоченные подмножества из 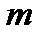 элементов,
элементов,  . Затем в каждом таком подмножестве упорядочим эти
. Затем в каждом таком подмножестве упорядочим эти 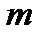 элементов. Получим всевозможные упорядоченные подмножества из
элементов. Получим всевозможные упорядоченные подмножества из  элементов, отличающиеся друг от друга либо составом элементов, либо порядком их следования.
элементов, отличающиеся друг от друга либо составом элементов, либо порядком их следования.
Число различных размещений из  элементов по
элементов по 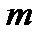 выражается формулой:
выражается формулой:
 . (5)
. (5)
Формулу (5) удобно записать в другой форме. Умножим и разделим произведение, стоящее в правой части формулы на 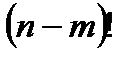 . Тогда получим
. Тогда получим
 , или
, или  (5*)
(5*)
Пример 12. Выпишем все размещения из четырех элементов  по два. Всего их 12:
по два. Всего их 12: 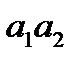 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 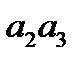 ,
, 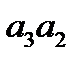 ,
, 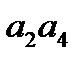 ,
, 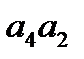 ,
,  ,
, 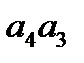 .
.
Такое же количество получается по формуле (5):  .
.
Пример 13. В группе 12 учеников. В классе 24 стула. Сколькими способами можно рассадить учеников в классе?
Решение. Различных способов размещения учеников на стульях, очевидно, столько же, сколько 12-ти элементных упорядоченных подмножеств 24-х элементного множества, то есть  способов.
способов.
Пример 14. Группа из 14 юношей и 15 девушек пошли в театр, но в кассе имеется лишь 20 билетов на один ряд. Сколькими способами можно распределить эти 20 билетов так, чтобы юноши и девушки чередовались?
Решение. 10 юношей можно посадить на нечетные места. Это задача о выборе и размещении 10 юношей из 14, следовательно, это можно сделать 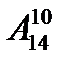 способами. 10 девушек можно посадить на четные места - это
способами. 10 девушек можно посадить на четные места - это 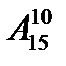 способов. Каждая из возможностей размещения девушек комбинирует с любой из возможностей размещения юношей. Следовательно, по правилу произведения, всего будет
способов. Каждая из возможностей размещения девушек комбинирует с любой из возможностей размещения юношей. Следовательно, по правилу произведения, всего будет 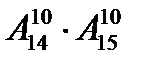 способов. Кроме того, такое же количество способов будет, если девушки займут нечетные места, а юноши - четные. По правилу сложения получаем всего
способов. Кроме того, такое же количество способов будет, если девушки займут нечетные места, а юноши - четные. По правилу сложения получаем всего  способов распределения билетов.
способов распределения билетов.
Пример 15. Сколько существует шестизначных чисел, делящихся на 5, в которых ни одна цифра не повторяется?
Решение. Если число делится на 5, то цифрами младшего разряда могут быть только 0 или 5. Рассмотрим два случая.
1случай. Если в младшем разряде стоит 0, то задача сводится к определению числа размещений 9 цифр на 5 мест. Для этого имеется  возможностей.
возможностей.
2 случай. Если в младшем разряде стоит 5, то в старшем разряде может быть любая цифра, кроме 0 и 5. Для этого имеется 8 возможностей. На оставшихся 4 местах нужно разместить 4 цифры из 8 оставшихся -  способов. Всего по правилу произведения этот случай дает
способов. Всего по правилу произведения этот случай дает  способов.
способов.
По правилу суммы окончательно получим Ответ:  способов.
способов.
Пример16. Какая часть из всевозможных семизначных телефонных номеров состоит из неповторяющихся цифр?
Решение. Поскольку телефонный номер по условию может начинаться с любой цифры, его можно рассматривать как элемент декартова произведения 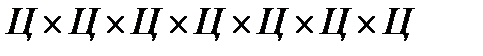 , где через
, где через  обозначено множество всех цифр от 0 до 9. Согласно правилу произведения, имеется
обозначено множество всех цифр от 0 до 9. Согласно правилу произведения, имеется  различных семизначных номеров.
различных семизначных номеров.
Число же номеров, состоящих из семи различных цифр, равно числу размещений 10 цифр на 7 мест -  . Тогда искомую часть можно вычислить как отношение
. Тогда искомую часть можно вычислить как отношение  .
.
3. Сочетания. Пусть 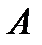 - некоторое конечное множество, состоящее из
- некоторое конечное множество, состоящее из 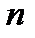 элементов. Будем строить из элементов этого множества всевозможные подмножества из
элементов. Будем строить из элементов этого множества всевозможные подмножества из  элементов. Получим соединения, которые называются сочетаниями. Число различных сочетаний из
элементов. Получим соединения, которые называются сочетаниями. Число различных сочетаний из 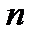 элементов по
элементов по 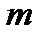 выражается формулой:
выражается формулой:
 (6)
(6)
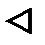 Доказательство. Составим все сочетания из
Доказательство. Составим все сочетания из  элементов по
элементов по 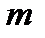 . Это можно сделать по определению
. Это можно сделать по определению  способами. В каждом из полученных сочетаний имеется
способами. В каждом из полученных сочетаний имеется  способов упорядочивания выбранных элементов (с помощью перестановки). Поэтому по правилу произведения имеем
способов упорядочивания выбранных элементов (с помощью перестановки). Поэтому по правилу произведения имеем  возможностей выбрать и разместить на
возможностей выбрать и разместить на 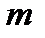 мест
мест 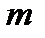 элементов из
элементов из  - элементного множества. С другой стороны, таких возможностей, как мы знаем, ровно
- элементного множества. С другой стороны, таких возможностей, как мы знаем, ровно  . Таким образом,
. Таким образом,  , откуда и следует формула (6).
, откуда и следует формула (6). 
Формулу (6) можно записать в более удобном для вычислений виде:
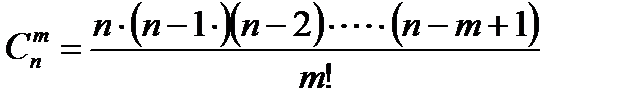 , или
, или
 (6*)
(6*)
Пример 17. Выпишем все сочетания из пяти элементов  по три.
по три.
Получим:  ,
,  ,
,  ,
, 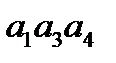 ,
,  ,
,  ,
,  ,
, 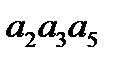 ,
,  ,
,  .
.
То же самое число различных сочетаний имеем и по формуле (6*) -  .
.
Пример 18. В выпуклом 12-угольнике проведены всевозможные диагонали, причем никакие три из них не пересекаются в одной точке. Сколько существует точек пересечения указанных диагоналей?
Решение. Каждой точке пересечения диагоналей соответствует 4 вершины 12-угольника, а каждой четверке вершин 12-угольника соответствует одна точка пересечения диагоналей, следовательно, число всех точек пересечения диагоналей равно числу способов, которыми можно из 12 вершин выбрать 4, то есть 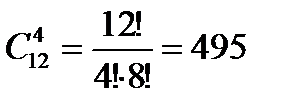 .
.
Пример 19. В чемпионате страны по футболу участвует 16 команд. Чемпионат проводится в два круга. Сколько всего командных игр? Ответ: 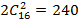 .
.
Пример 20. В урне находится 4 белых и 3 красных шара. Из урны одновременно вынимается два шара. Сколькими способами можно выбрать из урны:
a) шары одинакового цвета; б) шары разных цветов?
Решение. В случае а) число способов по правилу сложения равно 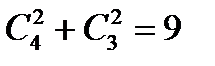 .
.
В случае б) число способов по правилу произведения есть  .
.
Пример 21. Полная колода карт (52 листа) делится случайным образом на две равные пачки по 26 листов. Сколькими способами можно поделить колоду так, что:
А) в каждой из пачек окажется по два туза; Б) в одной из пачек не будет ни одного туза; В) в одной из пачек будет один туз, а в другой - три?
Решение. В случае А) любые два туза из четырех можно выбрать  способами, а 24 оставшиеся карты из 48 -
способами, а 24 оставшиеся карты из 48 -  способами. По правилу произведения всего имеется
способами. По правилу произведения всего имеется  способов деления колоды.
способов деления колоды.
В случае Б) деление может осуществляться двумя способами: либо в первой пачке будет 4 туза, а во второй - ни одного, либо наоборот. Поэтому имеем  .
.
В случае В) аналогично имеем 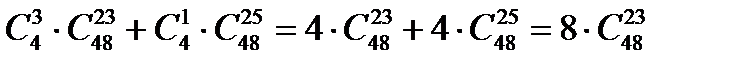 .
.
Если сравнивать количество способов деления, то получим  .
.
Другими словами, число случаев, когда колода делиться так, что в одной пачке будет три туза, а в одной один в 4,5 раза больше, чем число случаев, когда в одной из пачек не будет ни одного туза.
Пример 22. В партии из 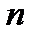 изделий имеется
изделий имеется  бракованных. Сколькими способами можно выбрать
бракованных. Сколькими способами можно выбрать  изделий так, чтобы среди них было ровно
изделий так, чтобы среди них было ровно  бракованных?
бракованных?
Решение. Выбрать 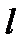 изделий из
изделий из 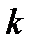 бракованных можно
бракованных можно  способами. Остальные
способами. Остальные  небракованных деталей из общего числа
небракованных деталей из общего числа 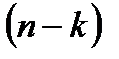 можно выбрать
можно выбрать  способами. По правилу произведения имеем
способами. По правилу произведения имеем  способов решения задачи.
способов решения задачи.
Пример 23. Сколькими различными способами можно нарисовать на шахматной доске размера  прямоугольник, стороны которого идут по границам клеток?
прямоугольник, стороны которого идут по границам клеток?
Ответ:  .
.
4. Размещения с повторениями. Подсчитываем число различных комбинаций, получаемых при размещении  типов элементов на
типов элементов на  мест, то есть число различных упорядоченных последовательностей длины
мест, то есть число различных упорядоченных последовательностей длины  , составленных из элементов
, составленных из элементов  типов:
типов: 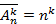 .
.
Пример 24. Сколько трехсимвольных «букв» можно составить из тире и точки?
Ответ:  .
.
5. Перестановки с повторениями. В этой схеме имеется 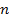 элементов, из которых
элементов, из которых 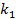 - одного типа,
- одного типа,  - второго типа, …,
- второго типа, …,  -
- 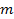 -го типа,
-го типа,  . Посчитаем число различных перестановок
. Посчитаем число различных перестановок  этих элементов. Если бы все элементы были различны, число перестановок составило бы
этих элементов. Если бы все элементы были различны, число перестановок составило бы 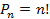 . При этом перестановки элементов внутри одного типа не дают новую конфигурацию, поэтому, умножая неизвестное пока число
. При этом перестановки элементов внутри одного типа не дают новую конфигурацию, поэтому, умножая неизвестное пока число  на количество перестановок повторяющихся элементов, мы получим общее число перестановок:
на количество перестановок повторяющихся элементов, мы получим общее число перестановок:
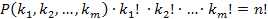 , откуда
, откуда 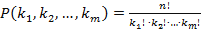 ,
,
Пример 25. Сколько различных «слов» можно получить, переставляя буквы в слове параллелограмм? Ответ.  .
.
Пример 26. Сколько кратчайших путей соединяют левый нижний и правый верхний углы шахматной доски? (Движение происходит по сторонам клеток)
Ответ.  .
.
Пример 27. Сколько существует способов раздать 52 карты четырем игрокам? Ответ. 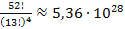 .
.
6. Сочетания с повторениями. В отличие от предыдущей схемы нас не интересует порядок выбора предметов, а лишь конечный результат. Из элементов 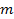 типов выбираются
типов выбираются 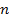 – элементные подмножества.
– элементные подмножества.
Каждое выбранное подмножество можно отождествить с упорядоченной последовательностью длины 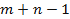 , в которой содержится
, в которой содержится 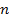 точек и
точек и 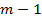 вертикальных черточек, разделяющих эти точки на
вертикальных черточек, разделяющих эти точки на 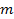 частей, причем количество элементов -го типа, попавших в выбранное подмножество равно числу точек между
частей, причем количество элементов -го типа, попавших в выбранное подмножество равно числу точек между 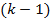 -ой и
-ой и  -ой черточками. Если между какими-либо соседними черточками нет точек, то элементы соответствующего типа не попали в выбранное множество.
-ой черточками. Если между какими-либо соседними черточками нет точек, то элементы соответствующего типа не попали в выбранное множество.
Получаем 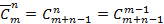 (число способов расставить
(число способов расставить 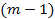 черточку, разделив ими
черточку, разделив ими 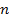 позиций)
позиций)
Например, следующий рисунок соответствует такому набору 6 элементов из 6 типов: 0 элементов первого типа, 2 – второго, 0 – третьего, 1-четвертого, 0 - пятого и 3 – шестого.
Пример 28. Сколько существует способов выбрать 10 пирожных, если в буфете имеются пирожные 3 видов. Ответ. 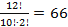 .
.
Пример 29. Сколько существует различимых результатов совместного бросания 3 одинаковых правильных игральных костей и 10 неразличимых монет одного достоинства. Ответ.  .
.