ЗАНЯТИЕ 10. Предельные теоремы теории вероятностей
Цель занятия: изучение двумерных дискретных векторов, их законов распределения и числовых характеристик.
Краткие теоретические сведения: двумерные дискретные векторы.
Пусть на одном и том же вероятностном пространстве ( , F, P) задано n случайных величин
, F, P) задано n случайных величин  ,
,  , …,
, …,  . Совокупность случайных величин
. Совокупность случайных величин 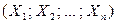 называется многомерной (n-мерной) случайной величиной, или (n-мерным) случайным вектором.
называется многомерной (n-мерной) случайной величиной, или (n-мерным) случайным вектором.
Пример 1. Широта X и долгота Y падения метеорита на Землю представляют собой двумерный случайный вектор  . В эту модель можно ввести также третью координату Z – время от начала наблюдений до момента падения первого метеорита на Землю. Тогда получится трехмерный случайный вектор
. В эту модель можно ввести также третью координату Z – время от начала наблюдений до момента падения первого метеорита на Землю. Тогда получится трехмерный случайный вектор  .
.
Пример 2. Успеваемость студента, окончившего курс обучения в вузе, характеризуется системой n случайных величин 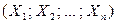 – оценками, проставленными в его дипломе.
– оценками, проставленными в его дипломе.
Рассмотрим на одном и том же вероятностном пространстве ( , F, P) несколько случайных величин
, F, P) несколько случайных величин 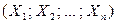 . Так как множества
. Так как множества  , т.е. являются событиями, то и их пересечение
, т.е. являются событиями, то и их пересечение  . Поэтому существует вероятность этого события.
. Поэтому существует вероятность этого события.
Многомерной функцией распределения  называется функция
называется функция  .
.
В дальнейшем изложении ограничимся случаем двух случайных величин  . Поэтому будем рассматривать
. Поэтому будем рассматривать  .
.
 Замечание 1. Геометрически значение
Замечание 1. Геометрически значение  – это вероятность попадания случайной точки
– это вероятность попадания случайной точки  в бесконечный квадрант с вершиной
в бесконечный квадрант с вершиной 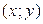 (на рис. 1 этот квадрант показан штриховкой).
(на рис. 1 этот квадрант показан штриховкой).
Замечание 2. С помощью  , можно вычислять вероятности попадания случайной точки в полуполосу или в прямоугольник:
, можно вычислять вероятности попадания случайной точки в полуполосу или в прямоугольник:
а)  (рис. 2 а);
(рис. 2 а);
б)  (рис. 2 б);
(рис. 2 б);
в) 
 (рис. 2 в);
(рис. 2 в);



а б в
Рис. 2.
Пример 3. Дана двумерная функция распределения: 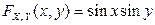 , где
, где  ,
,  . Найти вероятность попадания случайной точки
. Найти вероятность попадания случайной точки  в прямоугольник, ограниченный прямыми
в прямоугольник, ограниченный прямыми  ,
,  ,
,  ,
,  .
.
Решение. 

 .
.
Ответ:  .
.
Из формулы вычисления вероятности попадания в прямоугольник и определения многомерной функции распределения  , вытекают ее свойства, которые доказываются аналогично одномерному случаю:
, вытекают ее свойства, которые доказываются аналогично одномерному случаю:
1.  по каждому аргументу не убывает и непрерывна слева.
по каждому аргументу не убывает и непрерывна слева.
2.  .
.
3.  .
.
4. а) При  двумерная функция распределения
двумерная функция распределения  становится функцией распределения компоненты X:
становится функцией распределения компоненты X:  .
.
б) При  двумерная функция распределения
двумерная функция распределения  становится функцией распределения компоненты Y:
становится функцией распределения компоненты Y:  .
.
Двумерная случайная величина  называется дискретной, если случайные величины Х и Y дискретны.
называется дискретной, если случайные величины Х и Y дискретны.
Если случайная величина Х может принимать только значения 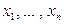 (для простоты изложения ограничимся только конечным множеством значений), а случайная величина Y – значения
(для простоты изложения ограничимся только конечным множеством значений), а случайная величина Y – значения  , то двумерный случайный вектор
, то двумерный случайный вектор  может принимать только пары значений
может принимать только пары значений  , где
, где  ,
, 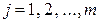 . Также как и в одномерном случае, распределение двумерной дискретной случайной величины естественно описывается с помощью таблицы:
. Также как и в одномерном случае, распределение двумерной дискретной случайной величины естественно описывается с помощью таблицы:
| Y X | 
| 
| … | 
| 
|

| 
| 
| … | 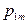
| 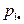
|

| 
| 
| … | 
| 
|
| … | … | … | … | … | … |

| 
| 
| … | 
| 
|

| 
| 
| … | 
| |
В этой таблице  и
и  .
.
Одномерные законы распределения отдельных компонент случайного вектора  выражаются через вероятности совместных значений
выражаются через вероятности совместных значений  по формулам:
по формулам:
 ,
,  ,
,
где суммирование распространяется на все возможные значения индексов i или j. Уточним, что для получения значения вероятности  для некоторого фиксированного значения i, надо сложить вероятности
для некоторого фиксированного значения i, надо сложить вероятности  , стоящие в i -ой строке таблицы, а для получения значения вероятности
, стоящие в i -ой строке таблицы, а для получения значения вероятности  для некоторого фиксированного значения j, надо сложить вероятности
для некоторого фиксированного значения j, надо сложить вероятности  , стоящие в j -ом столбце таблицы. При этом удобно одномерные законы распределения отдельных компонент записывать в той же таблице (см. ее последнюю строку и последний столбец). В правом нижнем углу таблицы обязательно должна находиться единица, являющаяся результатом суммирования вероятностей в ее последней строке (последнем столбце) и соответствующая условию нормировки. С помощью таблицы нетрудно определить функцию распределения
, стоящие в j -ом столбце таблицы. При этом удобно одномерные законы распределения отдельных компонент записывать в той же таблице (см. ее последнюю строку и последний столбец). В правом нижнем углу таблицы обязательно должна находиться единица, являющаяся результатом суммирования вероятностей в ее последней строке (последнем столбце) и соответствующая условию нормировки. С помощью таблицы нетрудно определить функцию распределения  .
.
Также легко по таблице вычисляется вероятность любого события B, задаваемого в виде произвольной области на плоскости:
 .
.
Пример 4. Закон распределения двумерного дискретного случайного вектора  задан таблицей:
задан таблицей:
| Y X | –1 | |
| 0,1 | 0,06 | |
| 0,3 | 0,18 | |
| 0,2 | 0,16 |
Найти: одномерные законы распределения компонент X и Y; вероятность  . Составить функцию распределения
. Составить функцию распределения  .
.
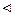 1) Одномерные законы
1) Одномерные законы  и
и  распределения компонент X и Y соответственно построены в таблице:
распределения компонент X и Y соответственно построены в таблице:
| Y X | –1 | 
| |
| 0,1 | 0,06 | 0,16 | |
| 0,3 | 0,18 | 0,48 | |
| 0,2 | 0,16 | 0,36 | |

| 0,6 | 0,4 |
2) 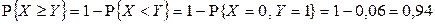 .
.
3) Согласно определению функции распределения  . Напомним, что геометрически значение
. Напомним, что геометрически значение  – это вероятность попадания случайной точки
– это вероятность попадания случайной точки  в бесконечный квадрант с вершиной
в бесконечный квадрант с вершиной 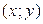 . Для вершины этого квадранта, согласно условию задачи, есть двенадцать областей, образованных тремя вертикальными прямыми
. Для вершины этого квадранта, согласно условию задачи, есть двенадцать областей, образованных тремя вертикальными прямыми  ,
, 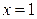 ,
,  и двумя горизонтальными прямыми
и двумя горизонтальными прямыми  ,
,  .
.
 На рис. 3 показан случай, когда вершина
На рис. 3 показан случай, когда вершина 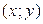 находится внутри прямоугольника
находится внутри прямоугольника  ,
,  . При этом внутри квадранта находится только одна точка с координатами
. При этом внутри квадранта находится только одна точка с координатами 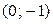 , в которой имеется ненулевая вероятность, равная 0,1. Функцию распределения
, в которой имеется ненулевая вероятность, равная 0,1. Функцию распределения  удобно задавать в виде таблицы (ее значение для случая, когда вершина
удобно задавать в виде таблицы (ее значение для случая, когда вершина 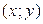 квадранта находится внутри прямоугольника
квадранта находится внутри прямоугольника  ,
,  выделено жирным шрифтом):
выделено жирным шрифтом):
| y x | 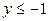
| 
| 
|

| |||

| 0,1 | 0,16 | |

| 0,4 | 0,64 | |

| 0,6 |
Пример 5. Известна функция распределения  двумерного дискретного случайного вектора
двумерного дискретного случайного вектора  :
:
| y x | 
| 
| 
| 
|

| ||||

| 0,5 | 0,5 | 0,5 | |

| 0,5 | 0,75 | 0,75 | |

| 0,5 | 0,75 | 0,875 | |

| 0,5 | 0,75 |
Составить функции распределения  и
и  компонент X и Y, а затем построить их законы распределения.
компонент X и Y, а затем построить их законы распределения.
 Решение. Учитывая, что
Решение. Учитывая, что  ,
,  , получим («проходя» соответственно по последнему столбцу и последней строке таблицы):
, получим («проходя» соответственно по последнему столбцу и последней строке таблицы):


Значит, для случайной величины X функция распределения испытывает «скачки» в точках  , для случайной величины Y – в точках
, для случайной величины Y – в точках  . Поэтому законы распределения компонент выглядят следующим образом:
. Поэтому законы распределения компонент выглядят следующим образом:
| X | Y | ||||||||

| 0,5 | 0,25 | 0,125 | 0,125 | 
| 0,5 | 0,25 | 0,25 |
Задачи для решения на занятиях:
Л-2, №№18.378, 18.385, 18.389, 18.411, 18.420.
Задачи на дом:
Л-2,№№ 18.383, 18.388, 18.390, 18.412, 18.416.