Геометрический смысл производной функции в точке.
Рассмотрим секущую АВ графика функции y=f(x) такую, что точки А и В имеют соответственно координаты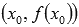 
и 
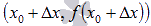, где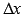 
- приращение аргумента. Обозначим через 
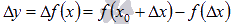приращение функции. Отметим все на чертеже:
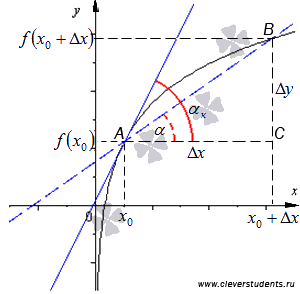
Из прямоугольного треугольника АВС имеем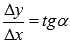 
. Так как по определению касательная – это предельное положение секущей, то 
.
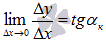Вспомним определение производной функции в точке: производной функции y=f(x) в точке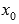 
называется предел отношения приращения функции к приращению аргумента при 
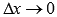, обозначается 
.
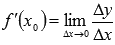Следовательно,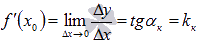 
, где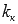 
- угловой коэффициент касательной.
Таким образом, существование производной функции y=f(x) в точке 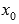эквивалентно существованию касательной к графику функции y=f(x) в точке касания 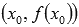, причем угловой коэффициент касательной равен значению производной в точке 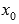, то есть 
.
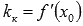Заключаем: геометрический смысл производной функции в точке состоит в существовании касательной к графику функции в этой точке.
К началу страницы
Уравнение касательной прямой.
Для записи уравнения любой прямой на плоскости достаточно знать ее угловой коэффициент и точку, через которую она проходит. Касательная прямая проходит через точку касания и ее угловой коэффициент для дифференцируемой функции равен значению производной в точке 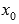. То есть, из пункта геометрический смысл производной функции в точке мы можем взять все данные для записи уравнения касательной прямой.
Уравнение касательной к графику функции y = f(x) в точке 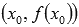имеет вид 
.
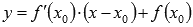Мы подразумеваем, что существует конечное значение производной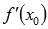 
, в противном случае касательная прямая либо вертикальна (есл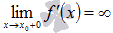и 
и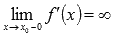 
), либо не существует (если 
).
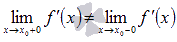В зависимости от углового коэффициента 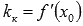, касательная может быть параллельна оси абсцисс (
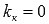), параллельна оси ординат (
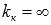в этом случае уравнение касательной будет иметь вид 
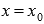), возрастать (
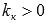) или убывать (
).
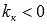Самое время привести несколько примеров для пояснения.
Пример.
Составить уравнение касательной к графику функции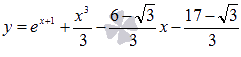 
в точке (-1;-3) и определить угол наклона.
Решение.
Функция определена для всех действительных чисел (при необходимости обращайтесь к статье область определения функции). Так как (-1;-3) – точка касания, то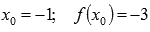 
.
Находим производную (для этого может пригодиться материал статьи дифференцирование функции, нахождение производной) и вычисляем ее значение в точке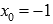 
:
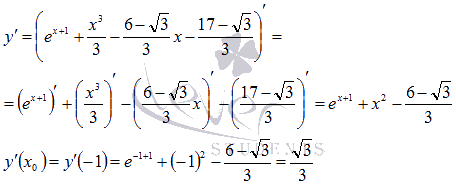
Так как значение производной в точке касания есть угловой коэффициент касательной, а он равен тангенсу угла наклона, то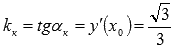 
.
Следовательно, угол наклона касательной равен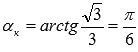 
, а уравнение касательной прямой имеет вид
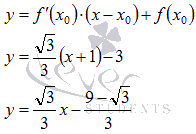
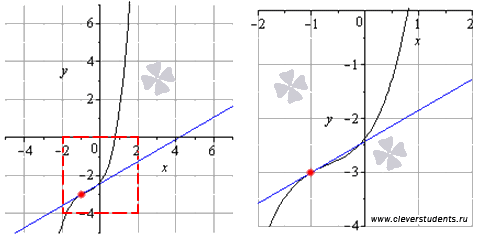
Графическая иллюстрация.
Черным цветом показан график исходной функции, касательная прямая изображена синей линией, точка касания - красной точкой. Рисунок справа представляет собой увеличенную область, обозначенную красным пунктирным квадратом на рисунке слева.
Пример.
Выяснить, существует ли касательная к графику функции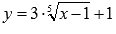 
в точке (1; 1), если да, то составить ее уравнение и определить угол ее наклона.
Решение.
Областью определения функции является все множество действительных чисел.
Находим производную:
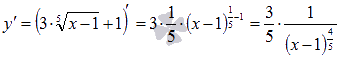
При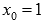 
производная не определена, но 
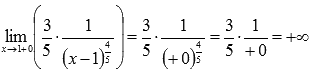и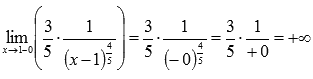 
, следовательно, в точке (1;1) существует вертикальная касательная, ее уравнение имеет вид x = 1, а угол наклона равен 
.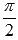