Определение производной.
Задачи, приводящие к понятию производной.
Физический и геометрический смысл производной.
Преподаватель математики
Мельник Павел Викторович
Тамбов 2020
Тема урока:
Определение производной. Задачи, приводящие к понятию производной. Физический и геометрический смысл производной.
Цели урока:
1) ввести понятие производной;
2) рассмотреть задачи, приводящие к понятию производной;
3) закрепить умение применять физический и геометрический смысл производной на конкретных примерах.
Ход урока.
I. Организационный момент (5 мин)
Вспомнить необходимые определения. Сообщить тему и цели урока.
II. Проверка домашнего задания. Актуализация знаний учащихся.(10 мин)
Два ученика у доски решают №21.24 (в,г) из домашнего задания, в это время идет фронтальный опрос, после которого обсуждается решение примеров на доске.
Фронтальный опрос.
- Дать определение функции.
- Дать определение предела функции на бесконечности. Геометрический смысл. (Графики на интерактивной доске Слайд №1)
- Дать определение предела функции в точке. Какая функция называется непрерывной в точке?
- Дать определение приращения аргумента и приращения функции.
III. Изучение нового материала. (20мин.)
Слайд №2
Понятие предела имеет большой философский смысл. Окружающий нас мир бесконечен, бесконечны пространство и время. Если какое-либо явление можно описать некоторым законом, т. е. функцией, то предел этой функции на бесконечности может нам многое «рассказать» о будущем этого явления.
Слайд №3
С понятием предела непосредственно связано понятие производной. Различные задачи из различных областей знания приводят к одной и той же математической модели – пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремиться к нулю. Впервые название этой модели и ее обозначение ввел немецкий ученый Готфрид Вильгельм Лейбниц в 1675 году – основоположник дифференциального и интегрального исчисления. Лейбниц был философом и лингвистом, историком и биологом, дипломатом и политическим деятелем, математиком и изобретателем. Он в 1700 году организовал академию в Берлине, он же рекомендовал Петру I организовать академию в России. При организации Петербургской Академии наук в 1725 г. пользовались планами Лейбница.
Слайд №4
Итак, определение производной:
Производная непрерывной функции в данной точке равна пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
f ′ (𝑥) =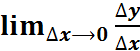 
.
Обозначается f ′(х) или df/ dx, где df – дифференциал функции,
dx - дифференциал аргумента (дифференциал – бесконечно малое приращение).
Если функция имеет производную в точке хо, то ее называют дифференцируемой в точке хо. Процедуру нахождения производной функции называют дифференцированием функции.
Мы рассмотрим две задачи, которые приводят к понятию производной.
Слайд №5
I. Механическая задача.
Итальянский ученый Г. Галилей, изучая свободное падение тел, экспериментальным путем определил зависимость пути S, пройденного телом за время t: S = gt2/2, где g – ускорение свободного падения. При свободном падении скорость тела v растет, движение неравномерное. Как найти скорость тела в любой момент времени, т.е. мгновенную скорость v(t)? Мы знаем, что при равномерном движении v=S/t. При неравномерном движении по этой формуле находится средняя скорость на всем пути: vср=∆S/∆t. Рассмотрим два момента времени: t и t+∆t, причем ∆t – малый промежуток времени. Тогда за этот промежуток времени тело пройдет путь ∆S=S(t+∆t) – S(t) и vср=∆S/∆t. Если ∆tà0, то vсрàv(t), значит.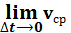 
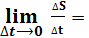= v(t), 
v(t)
Вывод. Физический смысл производной заключается в том, что мгновенная скорость – это производная пути по времени:
v = S′ (t)
Вспомним определение ускорения: а = ∆v/∆t, но если ∆tà0, то
а =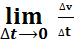 
Итак, задача механики о нахождении скорости тела в любой момент времени решена. Нужно только вычислить предел отношения приращения пути к приращению времени, если приращение времени стремится к нулю, т. е. найти производную пути.
II. Еще одна задача, приводящая к понятию производной, – задача о касательной к графику функции 𝒚 = f(𝑥).
Слайд №6
Рассмотрим график непрерывной функции и проведем в точке А секущую и касательную к графику
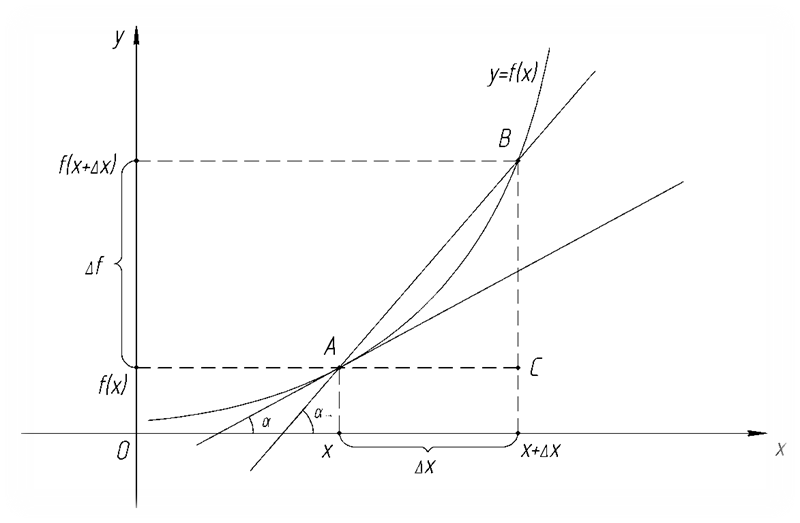
Прямая АВ – секущая, ee уравнение y = kсекх +b, где kсек – угловой коэффициент секущей,
kсек =∆y/∆x = tg αсек, где αсек – угол наклона секущей (отсчитывается от положительного направления оси Ох против часовой стрелки).
Пусть ∆х стремится к нулю, тогда секущая стремится к своему предельному положению – к касательной в точке А, т. е. угловой коэффициент касательной равен пределу углового коэффициента секущей: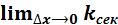 
= kкас, причем kкас = tg α, где α - это угол наклона касательной, отсчитываемый от положительного направления оси Ох.
Значит, kкас = tg α =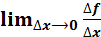 
Вывод. Геометрический смысл производной заключается в том, что угловой коэффициент или тангенс угла наклона касательной к графику функции в данной точке с абсциссой 𝑥 равен производной функции в этой точке:
kкас = tg α = f ′ (𝑥)
IV.Закрепление изученного материала. (5 мин)
Устно решаются номера 22.4, 22.12-22.14(в,г) из учебника: Математика.10 класс. А. Г. Мордкович, И. М. Смирнова.- М.:Мнемозина, 2007.
Домашнее задание: §22, № 22.4, 22.12-22.14(а,б).