Определение 1. Ряд вида
, (37)
где функции 
определены на некотором множестве 
, называется 
кратным функциональным рядом, а суммы вида
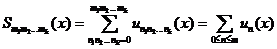
называются его частными суммами.
Здесь и в последующем 
, 
, неравенства вида 
, 
означают соответственно 
, 
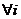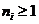
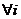, а неравенство 
- что 
.
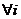Определение 2. Ряд (37) называется сходящимся на множестве , если при каждом фиксированном 
кратный числовой ряд
сходится. Если ряд (37) сходится на , то функция
, 
называется его суммой.
Частным случаем кратных функциональных рядов являются кратные степенные ряды.
Определение 3. Ряды вида
,
где 
- вообще говоря, комплексные числа, называются кратными степенными рядами.
Замена переменной 
, т. е. 
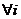сводит этот ряд к простейшей форме:
.
На кратные степенные ряды переносятся все результаты, доказанные для двойных степенных рядов. Методы доказательств этих результатов остаются прежними. Усложнятся лишь записи при переходе к кратным рядам.
На кратные функциональные ряды легко переносится понятие равномерной сходимости, признак Вейерштрасса равномерной сходимости и т. п. Формально эти понятия и теоремы выглядят так же, как и для простых функциональных рядов.
Определение 4. Ряд (37), члены которого являются функциями, определенными на множестве , называются равномерно сходящимися на этом множестве, если последовательность его частных сумм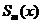 
равномерно сходится на , т.е. существует функция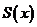 
, определенная на такая, что для любого 
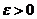найдется номер 
, такой, что 
, 
.
Равномерную сходимость обозначают символически так: 
, .
Критерий Коши равномерной сходимости ряда. Для того чтобы ряд (37) равномерно сходился на множестве , необходимо и достаточно, чтобы для любого 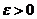существовал такой номер 
, что для всех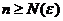 
и всех целочисленных 
и всех выполнялось неравенство
здесь 
, 
, 
, 
.
Следствие. (необходимое условие равномерной сходимости).
Если ряд (37) равномерно сходится, то 
на .
Теорема Вейерштрасса. Пусть даны два ряда: функциональный (37), члены которого определены на множестве , и числовой
, 
, 
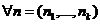(38)
Если ряд (38) сходится и 
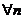, то ряд (37) абсолютно и равномерно сходится на множестве .
Доказательства этих теорем проводятся так же, как для простых функциональных рядов.
Основываясь на этих теоремах, легко доказать также, как и для простых рядов следующие свойства.
Свойства простых степенных рядов.
Пусть степенной ряд
(39)
имеет область сходимости 
. Тогда
1) В любой замкнутой подобласти 
ряд (39) сходится равномерно.
2) Сумма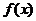 
степенного ряда (39) для всех 
является непрерывной функцией.
3) Если два степенных ряда 
и 
в окрестности точки 
имеют одну и ту же сумму, то эти ряды тождественны, т. е. 
.
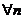4) Если степенной ряд (39) расходится в точке 
, то на луче 
его сходимость не может быть равномерной.
5) Если степенной ряд сходится в точке , то его сходимость равномерна на луче .
6) Степенной ряд (39) в прямоугольнике 
можно интегрировать почленно ()
.
7) Степенной ряд (39) внутри области сходимости 
можно почленно дифференцировать по каждой переменной.
8) Степенной ряд (39) по отношению к функции 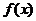является ее рядом Тейлора.