1. Найти общее решение линейного неоднородного дифференциального уравнения первого порядка двумя методами (методом вариации произвольной постоянной и методом Бернулли), а затем найти частное решение, удовлетворяющее заданному начальному условию:
а) 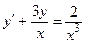 ,
,  ; б)
; б) 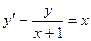 ,
,  ; в)
; в)  ,
,  ; г)
; г) 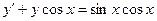
 ; д)*
; д)* 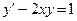 ,
,  .
.
Тема 21. Линейные дифференциальные уравнения
второго порядка с постоянными коэффициентами
Определение 1. Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами называют дифференциальное уравнение вида
 , (21.1)
, (21.1)
где  ,
,  ,
,  – постоянные числа,
– постоянные числа, 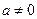 , функция
, функция 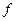 определена и непрерывна на некотором интервале
определена и непрерывна на некотором интервале 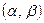 ,
,  .
.
Определение 2. Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называют дифференциальное уравнение вида
 . (21.2)
. (21.2)
Определение 3. Если в дифференциальном уравнении (21.1)  , то уравнение вида (21.2) называют линейным однородным дифференциальным уравнением второго порядка, соответствующим неоднородному линейному дифференциальному уравнению (21.1).
, то уравнение вида (21.2) называют линейным однородным дифференциальным уравнением второго порядка, соответствующим неоднородному линейному дифференциальному уравнению (21.1).
Замечание 1. Дифференциальные уравнения (21.1) и (21.2) удовлетворяют теореме о существовании и единственности решения дифференциального уравнения второго порядка.
Замечание 2. Начальные условия для дифференциального уравнения второго порядка имеют вид 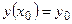 ,
,  . Задача Коши дифференциального уравнения второго порядка формулируется следующим образом: найти решение дифференциального уравнения, удовлетворяющее начальным условиям
. Задача Коши дифференциального уравнения второго порядка формулируется следующим образом: найти решение дифференциального уравнения, удовлетворяющее начальным условиям 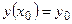 ,
,  .
.
Свойства решений линейного однородного
дифференциального уравнения первого порядка
1. Функция  всегда является решением линейного однородного дифференциального равнения второго порядка.
всегда является решением линейного однородного дифференциального равнения второго порядка.
2. Если функции  и
и 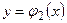 являются решениями линейного однородного дифференциального уравнения второго порядка, то функции
являются решениями линейного однородного дифференциального уравнения второго порядка, то функции  и
и 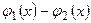 также являются его решениями.
также являются его решениями.
3. Если функция  является решением линейного однородного дифференциального уравнения второго порядка, а
является решением линейного однородного дифференциального уравнения второго порядка, а 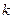 – любое число, отличное от нуля, то функция
– любое число, отличное от нуля, то функция  также является его решением.
также является его решением.
21.1. Общее решение линейного однородного
дифференциального уравнения второго порядка
с постоянными коэффициентами
Определение 4. Функции  и
и  , определенные на некотором интервале
, определенные на некотором интервале 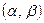 , называют линейно зависимыми на интервале
, называют линейно зависимыми на интервале 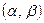 , если существуют вещественные числа
, если существуют вещественные числа 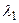 и
и  , не все одновременно равные нулю, что для любого
, не все одновременно равные нулю, что для любого 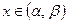 справедливо равенство
справедливо равенство 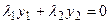 .
.
Определение 5. Если для любого 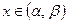 равенство
равенство 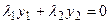 выполняется только при
выполняется только при 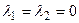 , то функции
, то функции  и
и  называют линейно независимыми на интервале
называют линейно независимыми на интервале 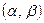 .
.
Определение 6. Два частных решения  и
и  уравнения (21.2) называют фундаментальной системой решений, если они линейно независимы.
уравнения (21.2) называют фундаментальной системой решений, если они линейно независимы.
Теорема 1. Если функции  и
и  образуют фундаментальную систему решений уравнения (21.2), то его общее решение имеет вид
образуют фундаментальную систему решений уравнения (21.2), то его общее решение имеет вид  , где
, где 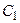 и
и  – вещественные произвольные постоянные.
– вещественные произвольные постоянные.
Определение 7. Характеристическим уравнением, соответствующим дифференциальному уравнению (21.2), называют алгебраическое уравнение вида  .
.
Алгоритм поиска общего решения
линейного однородного дифференциального уравнения
второго порядка с постоянными коэффициентами
1) Составить характеристическое уравнение, соответствующее данному дифференциальному уравнению.
2) Найти корни характеристического уравнения.
3) Выписать фундаментальную систему решений данного дифференциального уравнения в соответствии с правилом:
– если дискриминант характеристического уравнения  , то характеристическое уравнение имеет два вещественных различных корня
, то характеристическое уравнение имеет два вещественных различных корня 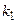 и
и 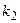 . Тогда фундаментальная система исходного дифференциального уравнения имеет вид
. Тогда фундаментальная система исходного дифференциального уравнения имеет вид 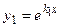 ,
,  ;
;
– если дискриминант характеристического уравнения  , то характеристическое уравнение имеет один вещественный корень кратности 2:
, то характеристическое уравнение имеет один вещественный корень кратности 2:  . Тогда фундаментальная система исходного дифференциального уравнения имеет вид
. Тогда фундаментальная система исходного дифференциального уравнения имеет вид  ,
,  ;
;
– если дискриминант характеристического уравнения  , то характеристическое уравнение имеет два комплексно-сопряженных корня
, то характеристическое уравнение имеет два комплексно-сопряженных корня  и
и 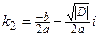 . Тогда фундаментальная система исходного дифференциального уравнения имеет вид
. Тогда фундаментальная система исходного дифференциального уравнения имеет вид  ,
,  .
.
4) Записать общее решение уравнения (21.2) в виде  , где
, где 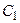 и
и  – вещественные произвольные постоянные. Записать ответ.
– вещественные произвольные постоянные. Записать ответ.
Пример 1. Найти общее решение дифференциального уравнения  .
.
Решение. Данное дифференциальное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
1) Его характеристическое уравнение имеет вид 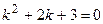 .
.
2) Так как  , то уравнение имеет два комплексно-сопряженных корня
, то уравнение имеет два комплексно-сопряженных корня 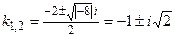 .
.
3) В соответствии с правилом фундаментальная система решений имеет вид  ,
,  .
.
4) Общее решение:  .
.
Пример 2. Найти частное решение дифференциального уравнения  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям  ,
,  .
.
Решение. Данное дифференциальное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
1) Его характеристическое уравнение имеет вид  .
.
2) Так как 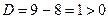 , то уравнение имеет два различных вещественных корня
, то уравнение имеет два различных вещественных корня  ,
,  .
.
3) В соответствии с правилом фундаментальная система решений имеет вид 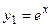 ,
,  .
.
4) Общее решение:  .
.
5) Найдем частное решение данного дифференциального уравнения, удовлетворяющего начальным условиям  ,
,  . Вычислим производную от общего решения:
. Вычислим производную от общего решения: 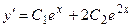 . Подставим в общее решение и его производную начальные условия
. Подставим в общее решение и его производную начальные условия  ,
,  :
:
 или
или 
Получили систему линейных алгебраических уравнений для определения 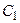 и
и  . Решая ее, получаем
. Решая ее, получаем 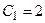 ,
,  . Тогда искомое частное решение примет вид
. Тогда искомое частное решение примет вид 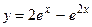 .
.
Пример 3. Найти решение задачи Коши  ,
,  ,
,  .
.
Решение. Данное дифференциальное уравнение является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
1) Его характеристическое уравнение имеет вид 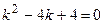 .
.
2) Так как  (или
(или  ), то уравнение имеет один вещественный корень кратности 2:
), то уравнение имеет один вещественный корень кратности 2: 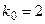 .
.
3) В соответствии с правилом фундаментальная система решений имеет вид 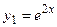 ,
,  .
.
4) Общее решение:  .
.
5) Найдем частное решение данного дифференциального уравнения, удовлетворяющего начальным условиям  ,
,  . Вычислим производную от общего решения:
. Вычислим производную от общего решения: 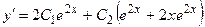 . Подставим в общее решение и его производную начальные условия
. Подставим в общее решение и его производную начальные условия  ,
,  :
:
 или
или 
Получили систему линейных алгебраических уравнений для определения 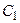 и
и  . Решая ее, получаем
. Решая ее, получаем 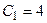 ,
,  . Тогда искомое частное решение примет вид
. Тогда искомое частное решение примет вид  .
.
21.2. Общее решение линейного неоднородного
дифференциального уравнения второго порядка
с постоянными коэффициентами
Теорема 2. Общее решение линейного неоднородного дифференциального уравнения (21.1) можно представить в виде суммы общего решения соответствующего линейного однородного дифференциального уравнения (21.2) и некоторого частного решения  неоднородного уравнения (21.1).
неоднородного уравнения (21.1).
Замечание. Для решения линейного неоднородного дифференциального уравнения второго порядка может быть применен общий метод вариации произвольных постоянных (см. [1, гл. 12, 12.8], [33, ч. 2, гл. 4, § 3], [35, гл. 4]). Но для достаточно большого числа случаев может быть использован метод подбора частного решения по виду правой части.
Теорема 3. Пусть дано дифференциальное уравнение  . Если функция
. Если функция  является частным решением уравнения
является частным решением уравнения  , а функция
, а функция  – частным решением уравнения
– частным решением уравнения 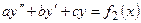 , то функция
, то функция  является частным решением
является частным решением  .
.
Алгоритм поиска общего решения
линейного неоднородного дифференциального уравнения
второго порядка с постоянными коэффициентами
1) Найти общее решение соответствующего однородного уравнения (21.2).
2) Подобрать частное решение неоднородного уравнения (21.1) в соответствии с правилом подбора частного решения по виду правой части.
Пусть 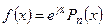 , где
, где  – известный многочлен степени
– известный многочлен степени 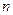 . Если
. Если  не является корнем характеристического уравнения, то частное решение следует искать в виде
не является корнем характеристического уравнения, то частное решение следует искать в виде  , где
, где  – многочлен степени
– многочлен степени 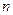 с пока неизвестными коэффициентами. Если
с пока неизвестными коэффициентами. Если  является простым корнем характеристического уравнения, то частное решение следует искать в виде
является простым корнем характеристического уравнения, то частное решение следует искать в виде  . Если
. Если  является корнем характеристического уравнения кратности 2, то частное решение следует искать в виде
является корнем характеристического уравнения кратности 2, то частное решение следует искать в виде  . Подставляя
. Подставляя  в уравнение (21.2) и приравнивая коэффициенты, стоящие слева и справа при одинаковых степенях
в уравнение (21.2) и приравнивая коэффициенты, стоящие слева и справа при одинаковых степенях  , найти коэффициенты многочлена
, найти коэффициенты многочлена  .
.
Пусть  или
или  , где
, где  – многочлен степени
– многочлен степени 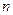 . Если
. Если  не являются комплексно-сопряженными корнями характеристического уравнения, то частное решение следует искать в виде
не являются комплексно-сопряженными корнями характеристического уравнения, то частное решение следует искать в виде 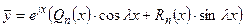 , где
, где  и
и  – различные многочлены степени
– различные многочлены степени 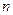 с пока неизвестными коэффициентами. Подставляя
с пока неизвестными коэффициентами. Подставляя  в уравнение (21.2) и приравнивая коэффициенты, стоящие слева и справа сначала соответственно при синусах и косинусах, а затем при одинаковых степенях
в уравнение (21.2) и приравнивая коэффициенты, стоящие слева и справа сначала соответственно при синусах и косинусах, а затем при одинаковых степенях  , найти коэффициенты многочленов
, найти коэффициенты многочленов  и
и  .
.
3) Записать общее решение неоднородного уравнения (21.1). Записать ответ.
Пример 4. Найти общее решение дифференциального уравнения 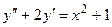 .
.
Решение. Данное дифференциальное уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
1) Выпишем соответствующее линейное однородное дифференциальное уравнение:  . Его характеристическое уравнение имеет вид
. Его характеристическое уравнение имеет вид 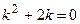 , его корни
, его корни 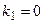 ,
, 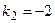 . В соответствии с правилом фундаментальная система решений состоит из функций
. В соответствии с правилом фундаментальная система решений состоит из функций 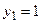 ,
,  . Общее решение линейного однородного дифференциального уравнения:
. Общее решение линейного однородного дифференциального уравнения:  .
.
2) Правая часть линейного неоднородного дифференциального уравнения представляет собой многочлен второй степени и может быть представлена следующим образом:  . Так как
. Так как  является простым корнем характеристического уравнения, то в соответствии с правилом подбора решения по виду правой части частное решение линейного неоднородного дифференциального уравнения следует искать в виде произведения многочлена второй степени с пока неизвестными коэффициентами на переменную
является простым корнем характеристического уравнения, то в соответствии с правилом подбора решения по виду правой части частное решение линейного неоднородного дифференциального уравнения следует искать в виде произведения многочлена второй степени с пока неизвестными коэффициентами на переменную  , то есть в виде
, то есть в виде 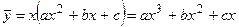 , где
, где  ,
,  и
и  – некоторые неопределенные вещественные коэффициенты. Найдем первую и вторую производные от частного решения
– некоторые неопределенные вещественные коэффициенты. Найдем первую и вторую производные от частного решения  , получим
, получим  ,
,  . Подставим частное решение
. Подставим частное решение  и его производные в линейное неоднородное дифференциальное уравнение
и его производные в линейное неоднородное дифференциальное уравнение 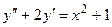 , тогда
, тогда
 или
или 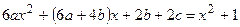 .
.
Приравнивая коэффициенты при одинаковых степенях  , получим систему линейных алгебраических уравнений для определения коэффициентов
, получим систему линейных алгебраических уравнений для определения коэффициентов  ,
,  и
и  :
:


Следовательно, искомое частное решение имеет вид
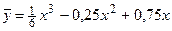 .
.
3) Таким образом, по теореме 2 общее решение исходного линейного неоднородного дифференциального уравнения: 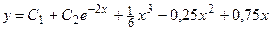 .
.
Пример 5. Найти решение задачи Коши линейного дифференциального уравнения  ,
,  ,
,  .
.
Решение. Данное дифференциальное уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами.
1) Выпишем соответствующее линейное однородное дифференциальное уравнение: 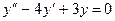 . Его характеристическое уравнение имеет вид
. Его характеристическое уравнение имеет вид 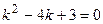 , его корни
, его корни  ,
, 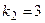 . В соответствии с правилом фундаментальная система решений состоит из функций
. В соответствии с правилом фундаментальная система решений состоит из функций 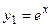 ,
,  . Общее решение линейного однородного дифференциального уравнения:
. Общее решение линейного однородного дифференциального уравнения:  .
.
2) Правая часть линейного неоднородного дифференциального уравнения представляет собой произведение многочлена первой степени на функцию  :
: 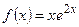 . Так как
. Так как 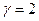 не является корнем характеристического уравнения, то в соответствии с правилом подбора решения по виду правой части частное решение линейного неоднородного дифференциального уравнения следует искать в виде произведения многочлена первой степени с пока неизвестными коэффициентами на функцию
не является корнем характеристического уравнения, то в соответствии с правилом подбора решения по виду правой части частное решение линейного неоднородного дифференциального уравнения следует искать в виде произведения многочлена первой степени с пока неизвестными коэффициентами на функцию  , то есть в виде
, то есть в виде  , где
, где  и
и  – некоторые неопределенные вещественные коэффициенты. Найдем первую и вторую производные от частного решения
– некоторые неопределенные вещественные коэффициенты. Найдем первую и вторую производные от частного решения  , получим
, получим
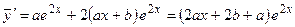 ,
,
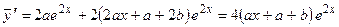 .
.
Подставим частное решение  и его производные в линейное неоднородное дифференциальное уравнение
и его производные в линейное неоднородное дифференциальное уравнение 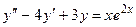 , получим равенство
, получим равенство
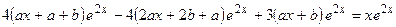 ,
,
которое после сокращения на  и приведения подобных слагаемых примет вид
и приведения подобных слагаемых примет вид

Приравнивая коэффициенты при одинаковых степенях  , получим систему линейных алгебраических уравнений для определения коэффициентов
, получим систему линейных алгебраических уравнений для определения коэффициентов  и
и  :
:
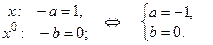
Следовательно, искомое частное решение имеет вид  .
.
3) Таким образом, по теореме 2 общее решение исходного линейного неоднородного дифференциального уравнения  .
.
Найдем решение задачи Коши. Для этого найдем производную от общего решения:  , а затем подставим начальные условия
, а затем подставим начальные условия  ,
,  в общее решение и его производную:
в общее решение и его производную:
 или
или 
Получили систему линейных алгебраических уравнений для определения 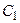 и
и  . Решая ее, получаем
. Решая ее, получаем  ,
, 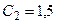 . Тогда искомое частное решение примет вид
. Тогда искомое частное решение примет вид  .
.
21.3. Математическая модель рынка
с прогнозируемыми ценами
В теме 10 была рассмотрена простейшая модель рыночного равновесия  , когда функции спроса
, когда функции спроса 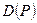 и предложения
и предложения 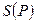 зависят только от текущей цены
зависят только от текущей цены  на товар. В реальных ситуациях спрос и предложение зависят также от тенденции ценообразования и темпа изменения цены. В моделях с непрерывной и дифференцируемой зависимостью цены от времени эти характеристики описываются, соответственно, первой и второй производными функции
на товар. В реальных ситуациях спрос и предложение зависят также от тенденции ценообразования и темпа изменения цены. В моделях с непрерывной и дифференцируемой зависимостью цены от времени эти характеристики описываются, соответственно, первой и второй производными функции  (
( – время). В этом случае функции спроса и предложения могут иметь вид
– время). В этом случае функции спроса и предложения могут иметь вид  ,
,  , где
, где 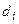 и
и  (
(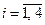 ) – вещественные числа. Записывая условие рыночного равновесия
) – вещественные числа. Записывая условие рыночного равновесия 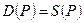 , получим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно равновесной цены
, получим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно равновесной цены 
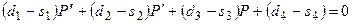 . (21.3)
. (21.3)
Равновесную цену  , определяемую дифференциальным уравнением (21.3), называют неустановившейся, так как значение
, определяемую дифференциальным уравнением (21.3), называют неустановившейся, так как значение  меняется с течением времени
меняется с течением времени  . Соответствующую модель рынка называют нестационарной или динамической. Если же значение цены
. Соответствующую модель рынка называют нестационарной или динамической. Если же значение цены  не зависит от времени
не зависит от времени  , то равновесную цену называют установившейся. Установившаяся равновесная цена
, то равновесную цену называют установившейся. Установившаяся равновесная цена  в динамической модели рынка определяется условием
в динамической модели рынка определяется условием  .
.
Замечание. Простейшая паутинная модель рыночного равновесия, рассмотренная в теме 10 (см. п. 10.5.1), является стационарной или статической моделью относительно установившейся равновесной цены.
По поведению неустановившейся равновесной цены  по отношению к установившейся равновесной цене
по отношению к установившейся равновесной цене  можно судить о состоянии рынка: стабильном или неустойчивом. Для этого достаточно вычислить
можно судить о состоянии рынка: стабильном или неустойчивом. Для этого достаточно вычислить 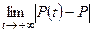 . Если окажется, что
. Если окажется, что 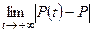 существует и равен нулю или не существует, но
существует и равен нулю или не существует, но 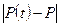 – периодическая функция, то состояния рынка стабильное. В этом случае неустановившаяся равновесная цена
– периодическая функция, то состояния рынка стабильное. В этом случае неустановившаяся равновесная цена  с течением времени достигнет установившейся равновесной цены
с течением времени достигнет установившейся равновесной цены  . Если окажется, что
. Если окажется, что 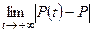 бесконечен или не существует и
бесконечен или не существует и  не является периодической функцией, то дифференциальное уравнение (21.3) описывает состояние паники на рынке. В этом случае равновесная цена
не является периодической функцией, то дифференциальное уравнение (21.3) описывает состояние паники на рынке. В этом случае равновесная цена  с течением времени будет только удаляться от установившейся равновесной цены
с течением времени будет только удаляться от установившейся равновесной цены  .
.
Пример 6. Функции спроса и предложения имеют вид 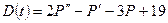 ,
,  . Найти неустановившуюся и установившуюся равновесные цены; выяснить, является ли стабильным состояние рынка.
. Найти неустановившуюся и установившуюся равновесные цены; выяснить, является ли стабильным состояние рынка.
Решение. 1) Найдем неустановившуюся равновесную цену. Из уравнения рыночного равновесия 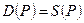 получим линейное неоднородное дифференциальное уравнение, позволяющее найти неустановившуюся рыночную цену:
получим линейное неоднородное дифференциальное уравнение, позволяющее найти неустановившуюся рыночную цену:
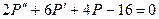 или
или  .
.
Выпишем соответствующее ему линейное однородное дифференциальное уравнение 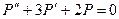 и характеристическое уравнение
и характеристическое уравнение  . Найдем корни характеристического уравнения:
. Найдем корни характеристического уравнения: 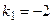 ,
, 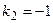 . Так как они вещественны и различны, то фундаментальная система решений линейного однородного дифференциального уравнения состоит из функций
. Так как они вещественны и различны, то фундаментальная система решений линейного однородного дифференциального уравнения состоит из функций  ,
,  , а его общее решение имеет вид
, а его общее решение имеет вид  . Правая часть исходного линейного неоднородного дифференциального уравнения может быть представлена следующим образом:
. Правая часть исходного линейного неоднородного дифференциального уравнения может быть представлена следующим образом:  . Так как
. Так как 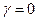 не является корнем характеристического уравнения
не является корнем характеристического уравнения  , то частное решение исходного линейного неоднородного дифференциального уравнения будем искать в виде
, то частное решение исходного линейного неоднородного дифференциального уравнения будем искать в виде  , где
, где 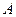 – некоторое, пока неизвестное, число. Вычислим
– некоторое, пока неизвестное, число. Вычислим 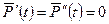 , подставим
, подставим  и его производные в дифференциальное уравнение
и его производные в дифференциальное уравнение  , получим
, получим 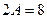 или
или  . Таким образом,
. Таким образом,  . В силу теоремы 2 запишем общее решение исходного линейного неоднородного дифференциального уравнения
. В силу теоремы 2 запишем общее решение исходного линейного неоднородного дифференциального уравнения  , которое представляет собой неустановившуюся рыночную цену.
, которое представляет собой неустановившуюся рыночную цену.
2) Найдем установившуюся рыночную цену. Для этого подставим  в дифференциальное уравнение
в дифференциальное уравнение  , получим, что
, получим, что  или
или 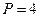 – установившаяся рыночная цена.
– установившаяся рыночная цена.
3) Оценим состояние рынка. Для этого вычислим  . Получим
. Получим
 .
.
Следовательно, состояние рынка стабильное.
 Замечание. Процесс приближения неустановившейся равновесной цены к установившейся показан на рис. 21.1. При построении функции
Замечание. Процесс приближения неустановившейся равновесной цены к установившейся показан на рис. 21.1. При построении функции 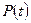 предполагалось, что в момент времени
предполагалось, что в момент времени  даны начальное значение неустановившейся равновесной цены
даны начальное значение неустановившейся равновесной цены  денежных единиц и начальное значение ее первой производной (скорость цены)
денежных единиц и начальное значение ее первой производной (скорость цены)  денежных единиц в единицу времени. Соответствующее частное решение имеет вид
денежных единиц в единицу времени. Соответствующее частное решение имеет вид 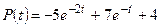 .
.
Теоретический материал: [1, гл. 12], [2, гл. 9], [3, гл. 9], [5], [8], [10], [12, гл. 19, 20], [17], [19], [21], [27], [33, ч. 2, гл. 4], [35, гл. 4].