Я часть контрольной работы
Вариант – 4
n - номер варианта в задачах 1, 3, 5. Задачи 2, 4 – общие для всех.
.
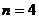1. В третьем семестре изучаются 11 дисциплин. Сколькими способами можно составить расписание на какой-либо день недели, если в этот день должны быть четыре пары по различным дисциплинам?
Решение:
Каждый вариант расписания представляет набор 4 дисциплин из 11, отличающийся от других вариантов как составом дисциплин, так и порядком их следования (или тем и другим), т.е. является размещением из 11 элементов по 4.
.
Ответ: 7920 способов.
2. Сколько шестизначных чисел, кратных пяти, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что цифры в числе не повторяются.
Решение:
Для того чтобы число, составленное из заданных цифр, делилось на 5, необходимо и достаточно, чтобы цифра 5 стояла на последнем месте. Остальные пять цифр могут стоять на оставшихся пяти местах в любом порядке. Следовательно, искомое число шестизначных чисел, кратных пяти, равно числу перестановок из пяти элементов, т.е.
.
Ответ: 120.
3. В чемпионате по футболу участвуют 14 команд, причем каждые две команды встречаются друг с другом дважды. Сколько матчей будет проведено?
Решение:
Число матчей в первом круге равно количеству сочетаний из 14 элементов по 2:
.
Во втором круге играется столько же матчей, поэтому в течение сезона состоится 182 встречи.
Ответ: 182 встречи.
4. Найти выражение для суммы первых N «треугольных» чисел
(написать формулу для N – го «треугольного» числа:
1, 3, 6, 10, 15, 21, 28,…
Решение:
Формула для N – го «треугольного» числа:
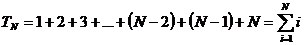или
.
Сумма конечного ряда треугольных чисел вычисляется по формуле:
.
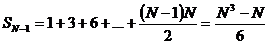5. Последовательность Фибоначчи задаётся рекуррентным соотношением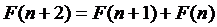 
и начальными условиями 
Найти выражение для общего члена последовательности и выписать её первые 13 членов.
Решение:
Данную последовательность можно задать рекуррентно:
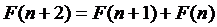и начальными условиями
Характеристическое уравнение для последовательности имеет вид
λ2 – λ – 1 = 0.
Найдем его корни:
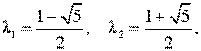
Поскольку корни характеристического уравнения вещественные и различные, то общее решение рекуррентного уравнения имеет вид
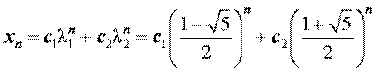
где c1 и c2 – произвольные действительные числа.
Найдем теперь значения произвольных постоянных c1 и c2 так, чтобы для последовательности
(*)
выполнялись начальные условия. Это означает, что числа c1 и c2 должны удовлетворять следующей системе из двух линейных уравнений с двумя неизвестными:
Решим полученную систему уравнений:
Для того, чтобы решить последнюю систему, вычтем первое уравнение из второго уравнения, оставив первое уравнение без изменений:
Подставляя найденные значения произвольных постоянных c1 и c2 в формулу (*), получаем искомую формулу общего члена последовательности Фибоначчи:
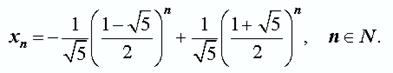
Первые 13 членов:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
я часть контрольной работы
.
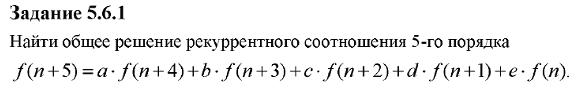
Решение:
Запишем характеристическое уравнение данного соотношения:
.
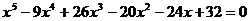Непосредственной подстановкой убеждаемся, что 
- корень характеристического уравнения.
Понизим степень многочлена поделив характеристический многочлен на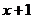 
:
В результате деления получим уравнение четвертой степени:
Заметим, что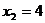 
является корнем этого уравнения, разделим левую часть уравнения на 
.
Получим уравнение третьей степени:
.
Заметим, что 
является корнем этого уравнения, разделим левую часть уравнения на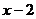 
.
Получим уравнение второй степени:
.
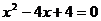Заметим, что 
является корнем этого уравнения.
По теореме о виде общего решения линейного рекуррентного соотношения с постоянными коэффициентами, запишем общее решение:
.