Метод начальных параметров для определения перемещений

Лекция №19

Тема: «Перемещения при изгибе»

Вопросы:

Дифференциальное уравнение изогнутой оси балки. Условие жесткости при изгибе

Метод начальных параметров для определения перемещений

Теорема о взаимности работ и взаимности перемещений

Дифференциальное уравнение оси изогнутого бруса

В результате изгиба балки ось становится криволинейной (см. рис. 1), центры поперечных сечений перемещаются от первоначальной прямой линии и поворачиваются на какой-то угол j (рис. 1). За прогиб 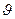принимают перемещение центра сечения перпендикулярно первоначальной оси. Для сечения К прогиб составит отрезок КК₁.

Для определения перемещений сечений балки пользуются дифферинциальным уравнением изогнутой оси балки:

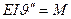(1)

где Е - модуль продольной упругости,

I - осевой момент инерции сечения,

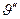- вторая производная от прогиба,

М - изгибающий момент.

В точке K₁ проведем касательную к изогнутой оси балки, которая образует с осью Z угол j, так как линии, образующие углы перпендикулярны. Из высшей математики известно, что первая производная от функции равна тангенсу угла наклона касательной, т.е.

.

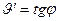Для малых значений угла справедливо равенство: tgj 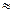j. Следовательно, первая производная от прогиба представляет собой угол поворота сечения.

 

Рис. 1

Проинтегрируем уравнение (11.1):

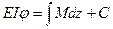(2)

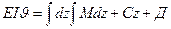(3)

где С и Д - постоянные интегрирования. Их находят из граничных условий. Для заданной балки при z=0; j=0; 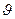=0. Подставив эти значения, находят С и Д.

По уравнению (3) можно найти максимальный прогиб , называемый стрелой прогиба f. Во избежании появления чрезмерных перемещений наибольший относительный прогиб f/l не должен превышать предельного значения f_и/l, устанавливаемого строительными нормами.

f/l£ f_и/l (4)

l - длина балки.

Это условие жесткости при изгибе. Расчет на жесткость производят по нормативной нагрузке, т.е. без учета возможной перенагрузки. Объясняется это тем, что конструкция должна обладать необходимой жесткостью в течение длительной эксплуатации, а не в критические моменты.

 

Метод начальных параметров для определения перемещений

Методом непосредственного интегрирования дифферинциального уравнения изогнутой оси балки сложно пользоваться, если балка имеет несколько участков. В общем случае, когда к балке приложена система нагрузок, делящих ее на n участков, для вычисления перемещений требуется составить n выражений изгибающего момента, дважды проинтегрировать n дифферинциальных уравнений и определить 2n произвольных постоянных. Причем выполнение последней операции кроме двух начальных условий необходимо рассмотреть еще 2(n -1) так называемых условий совместности (неразрывности) перемещений на границах смежных участков. В результате задача становится очень сложной уже при наличии трех участков. Поэтому в таких случаях прибегают к рационализации аналитического способа определения перемещений.

Условимся: 1)интегрирование составленных выражений, содержащих скобки, производить без раскрытия скобок; 2)при наличии сосредоточенного момента m его значение представлять в виде произведения m(z-a)⁰, где a - расстояние от начала координат до сечения, где приложен момент (записанное произведение равно m, поскольку любая величина в нулевой степени равна единице); 3)при действии распределенной нагрузки, не доходящей до правого конца балки, ее продолжают до этого конца, уравновешивая противоположно направленной нагрузкой той же интенсивности.

Выполнение перечисленных условий позволяет ограничиться составлением и интегрированием всего лишь одного дифферинциального уравнения - уравнения последнего участка балки. В результате этого, количество постоянных интегрирования оказывается равным двум независимо от числа участков. Уравнение для любого промежуточного участка может быть получено из уравнения последнего участка путем исключения слагаемых, которые содержат нагрузки, приложенные за пределами рассматриваемой части балки.

Составим уравнения изгибающих моментов для консольной балки. Все нагрузки зададим так, чтобы изгибающие моменты были положительными, что упростит вывод формулы (см. рис. 2, а).

Поместим начало координат на левом конце балки.

Распределенную нагрузку продлим до правого конца и приложим сверху балки компенсирующую нагрузку q (см. рис. 2, б).

.

Дифферинциальное уравнение изогнутой оси балки будет иметь вид:

.

а)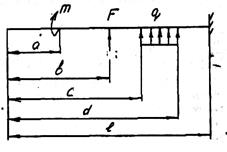
б)

Рис. 2

Произведем интегрирование:

.

где С - постоянная интегрирования. Ее можно определить, приняв z=0, j=j₀, тогда ₀= С, так как все члены уравнения, содержащие z, отбрасываются.

Уравнение примет вид:

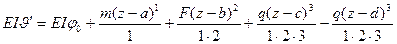. (5)

Проинтегрировав уравнение (11.5), получим:

,

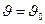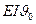где Д - постоянная интегрирования. При z=0; и =Д.

Уравнение запишется как:

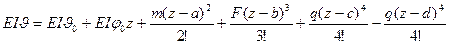(6)

Как видно, в уравнениях (5) и (6) степень переменной совпадает с факториалом.

В этих уравнениях неизвестны только начальные угол поворота сечения и прогиб , поэтому метод называется методом начальных параметров. Их находят из конечных условий. Для данной балки при z=l; =0 и 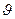=0. Подставив эти значения в уравнения (5) и (6), находят и .

В реальных условиях на балку может действовать несколько внешних моментов, сил и распределенных нагрузок, причем они могут создавать и отрицательные изгибающие моменты. Поэтому в общем случае уравнения примут вид:

(7)

(8).