Существование элемента наилучшего приближения

Теорема. Для любого элемента fÎR в 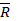существует элемент наилучшего приближения.

Доказательство. Пусть

Зафиксируем f и заставим пробегать Ф все пространство 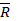- при этом у функции g, h будут изменяться коэффициенты a_i. Докажем непрерывность функций g, h.

Рассмотрим функцию g.

Зафиксируем некоторую точку и оценим разность:

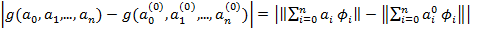
По свойствам нормы 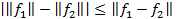(доказательство: ||f₁||=||f₂+(f₁-f₂)||£||f₂||+||f₁-f₂||, ||f₂||=||f₁+(f₂-f₁)||£||f₁||+||f₂-f₁||) Þ | ||f₂||- ||f₁|| |£ ||f₂-f₁||)

Отсюда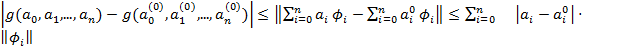

Непрерывность функции g означает, что .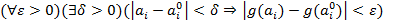

Обозначим , возьмем 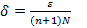и неравенство при этих условиях выполняется. Функция h³0. Пусть m=inf[h(a_i)] -точная нижняя грань. Докажем, что найдутся такие a_i, при которых эта точная нижняя грань достигается. Рассмотрим множество точек 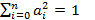-единичная сфера пространства. Это ограниченное замкнутое множество, следовательно, по теореме Кантора непрерывная положительная функция f должна достигать своей нижней границы m в этом пространстве. m¹0, так как 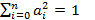. Следовательно, 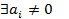такие, что 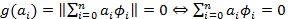(аксиома нормы).

Пусть . Разобьем пространство 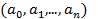на две части: R₁ и R₂.

R₁ - все точки, у которых ;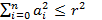

R₂ - все точки, у которых ;

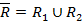
Рассмотрим значения функции h 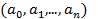на множестве R₂. Здесь 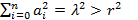и h =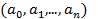

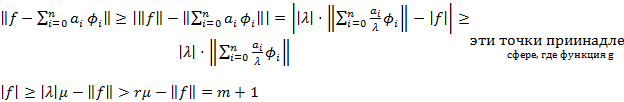
Это означает, что на множестве R₂ m не является точной нижней границей, а значит, m не является точной нижней гранью R₁. Но множество R₁ ограничено и замкнуто, а функция h - непрерывная, значит, она обязана достигать в некоторой точке своей нижней грани (непрерывный образ компакта есть компакт). Обозначим эту точку через и .

Итак, в 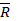существует элемент наилучшего приближения.

Определение. Множество называется строго нормированным, если в условии знак равенства достигается только тогда, когда , a>0.

Теорема. Достаточный признак единственности элемента наилучшего приближения.

Если пространство R строго нормировано, то элемент наилучшего приближения является единственным.

Доказательство. Пусть существуют два различных элемента наилучшего приближения для fÎR: и .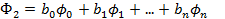

так как Ф₁ и Ф₂ - элементы наилучшего приближения, 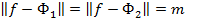. (m¹0, так как иначе бы оказались бы линейно зависимыми).

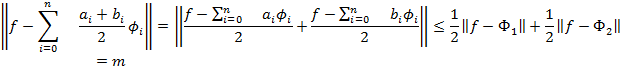
Так как норма, стоящая в левой части не может быть меньше m, то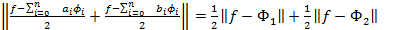

В силу того, что пространство R строго нормировано,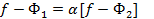

, так как иначе f выражалась бы в виде линейной комбинации 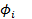. Следовательно, m=0, а значит Ф₁=Ф₂.

Определение. Назовём систему функций системой Чебышева на отрезке [a,b], если любой обобщенный многочлен (линейная комбинация этих функций) по этой системе, у которого хотя бы один из коэффициентов отличатся от 0, имеет на [a,b] не более n нулей.

Утверждение. Функции 1, x, x², x³,..., xⁿ образует систему Чебышева на любом отрезке [a,b].

Пусть H_n(P) - множество всех алгебраических многочленов степени n.

Число 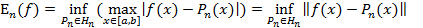называется наименьшим отклонением, или наилучшим приближением.

Теорема Хаара. Для того чтобы для любой заданной функции f(x)ÎC[a,b] существовал единственный обобщенный многочлен наилучшего приближения, необходимо и достаточно, чтобы функции образовали систему Чебышева.

(без доказательства)

На основании теоремы Хаара можно утверждать, что существует единственный многочлен P_n(x)ÎH_n(x), для которого 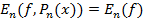отклонение от функции f будет наименьшим.

Определение. Пусть P_n(x) - полином наилучшего приближения для функции f(x)ÎC[a,b], то есть 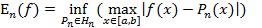. Тогда 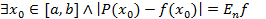. Такую точку будем называть (е) - точкой.

Если P(x₀)-f(x₀)=E_nf, то x0 называется (+) -точкой;

Если P(x₀)-f(x₀)=-E_nf, то x0 называется (-) -точкой

 

Теорема Чебышева. Пусть функция f(x)ÎC[a,b] и f(x)ÏH_n(P),то есть не является алгебраическим многочленом степени n.

Тогда:

1) существуют как (+) –точки, так и (-) –точки;

2) существует последовательность из (n+2) точек, которые попеременно являются (+) и (-) точками. Эту последовательность из (n+2) точек называют Чебышевским альтернансом.

Говорят также, что функция альтернирует P(x_i)-f(x_i)=(-1)²E_nf

Замечание. Пусть Ф(x) -некоторый обобщенный многочлен и на [a,b] существуют n+2 точки , что разность f(x_i)- Ф(x_i) принимает в них значения с чередующимися знаками. Тогда если m - наименьшее из значений |f(x_i)- Ф(x_i)|, то

Пример. Пусть функция f(x)ÎC[a,b] приближается многочленом нулевой степени. Пусть , .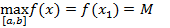

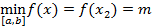Многочлен 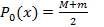является многочленом наилучшего равномерного приближения, x₁, x₂ - точками чебышевского альтернанса, причем .

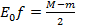m

M

(M+m)/2

a

b

P0(x)

x1

x2

Пример 2. Выпуклая дифференцируемая на [а,b] функция f приближается многочленом P₁(x)=a₀+a₁x. Вследствие выпуклости f разность f(x)-(a₀+a₁x) может иметь только одну точку экстремума на интервале (a,b). Поэтому точки a,b являются точками Чебышевского альтернанса. Пусть с(a,b) ​–третья точка альтернанса. Согласно теореме Чебышева должны выполняться условия f(a)-(a₀+a₁a)=R, f(c)-(a₀+a₁c)=-R, f(b)-(a₀+a₁b)=R, где R= s||P₁(x)-f(x)||_С[a,b] неизвестно. Из первого и второго условия получаем a₁=(f(b)-f(a))/(b-a). Точка c является точкой экстремума разности f(x)-(a₀+a₁x) и ищется из уравнения f^/(c)-a₁=0. Далее из первого и второго уравнений определяются a₀ и E₁f=|R|.

Геометрически решение данной задачи сводится к следующему:

1. Проводится хорда с наклоном a₁. 2. С этим же наклоном проводится касательная к кривой y. 3. Строится секущая посередине между хордой и касательной, дающая среди всех этих прямых наилучшее равномерное приближение кривой y=f(x) на отрезке [a,b].

Пример 2. Выпуклая дифференцируемая на отрезке [1,2] функция f(x)= 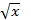приближается многочленом первой степени Р₁(x)=a₀+a₁x.

f(x)-(a₀+a₁x) также выпуклая, разность может иметь только одну точку экстремума на отрезке [1,2], поэтому точки a=1 и b =2 являются точками чебышевского альтернанса.

 

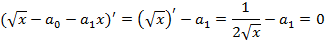
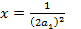-третья точка чебышевского альтернанса, c=x.

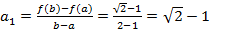и

;

 

Таким образом из первого и второго уравнения получаем a₀.

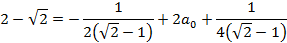
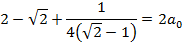
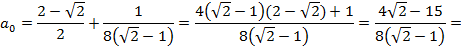
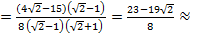-0,483757211

 

Геометрически решение данной задачи сводится к следующему:

1. Проводится хорда с наклоном a₁. Затем с этим же наклоном проводится касательная к кривой y. Наконец, строится секущая посередине между хордой и касательной, дающая среди всех прямых наилучшее равномерное приближение кривой y=f(x) на отрезке [a,b].

В общем случае построение многочлена наилучшего равномерного приближения затруднено, поэтому находят многочлен, близкий к наилучшему либо находят многочлен, дающий равномерное приближение с требуемой точностью e³0, т.е. удовлетворяющего условию 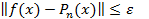. Такой P_n(x) не является наилучшим приближением.

Способы нахождения многочленов, близких к наилучшему.

1. Если f(x)ÎC[a,b], а fⁿ⁺¹ - производная n+1 - порядка, которая мало изменяется на интервале [a,b], то интерполяционный многочлен Лагранжа L_n(x) с чебышевскими узлами является близким к наилучшему.

2. Метод, применимый для функций, разлагающихся в ряд Тейлора.

пусть требуется приблизить равномерно функцию f(x)=arctg(x) на отрезке [-a,a], где 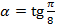с точностью 0,5×10^-5 . Берем сначала отрезок ряда Тейлора, аппроксимирующий данную функцию с несколько более высокой точностью, чем заданная.

Полагаем .

При этом . Подстановкой x=at переходим к отрезку [-1;1]:

Чтобы понизить степень, добавим к S₁₁(t) многочлен Чебышева 0,0000056×2^-10T₁₁(t). Получим

Имеем:

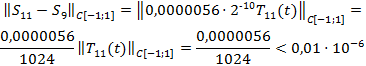
Таким образом, многочлен S₉(t) уклоняется на отрезке [-1;1] от многочлена S₁₁(t) на величину, которая значительно меньше, чем максимальное по модулю значение старшего члена у многочлена S₁₁(t) при t=±1. Поэтому такой способ понижения степени предпочтительней, чем отбрасывание старшего члена.

Поступая аналогично ещё два раза, находим

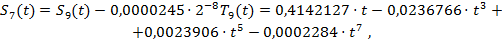
где T₇(t), T₉(t) - многочлены Чебышева: ,

.

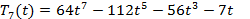При этом

;

.

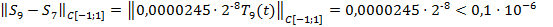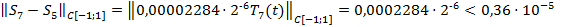Вернемся к первоначальной переменной x:

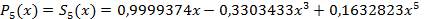, причем

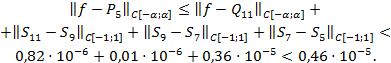
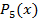-искомый многочлен, аппроксимирующий равномерно функцию arctg x на отрезке [-tg(p/8); tg(p/8)] с заданной точностью 0,5×10^-5.

Замечание. Многочлен Тейлора 7 степени такую точность не обеспечивает.

 

Метод наименьших квадратов.

Определение. Линейное пространство F с введенным на нем скалярным произведением (f,g) наз евклидовым пространством и обозначается через E.

Рассмотрим пространство непрерывных на [a,b] функций со скалярным произведением

и линейное пространство E_n+1 функций, заданных на конечном (дискретном) множестве точек x₀, x₁,..., x_n некоторого отрезка [a,b] со скалярным произведением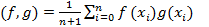

Функцию fÎ E_n+1 можно считать n+1 -мерным вектором f=(f₀, f₁,..., f_n), где f_i=f(x_i). (Проверить выполнение аксиом скалярного произведения: 1) (f,g)=(g,f) 2) (f,f)³0, (f,f)=0 Û f=Q 3)(a f,g)=a (f,g) 4) (f₁+f₂,g)=(f₁,g) +(f₂,g))

Следствие. Всякое евклидово пространство одновременно является линейным нормированным пространством с нормой 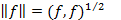, а значит, и метрическим пространством с расстоянием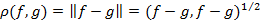

(Проверить 3 аксиомы нормы).

Определение. Пусть в евклидовом пространстве E дана система функций . Тогда определитель

составленный из скалярных произведений, называется определителем Грамма системы функций .

Лемма 1. Определитель Грамма равен нулю тогда и только тогда, когда система функций линейно зависима.

(Док сам-но)

Определение. система функций называется ортогональной, если 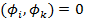, j¹k; 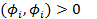, 0£j,k£m.

Утв. Если система функций ортогональна, то она линейно независима (мет от против)

Многочлен наилучшего среднеквадратичного приближения.

Определение. Функция Ф_m(x)= 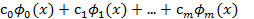, где c₀, c₁,..., c_m - числовые коэффициенты, называется обобщенным многочленом по системе функций .

Определение. Пусть произвольная функция f принадлежит евклидову пространству E. Ставится задача нахождения такого многочлена Ф_m(x), что расстояние 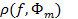, называемое также среднеквадратичным уклонением многочлена Ф_m(x) от функции f, минимально. Такой многочлен называется многочленом наилучшего среднеквадратичного приближения функции f.

Теорема. Если система функций линейно независима, то для любой функции fÎE многочлен наилучшего среднеквадратичного приближения существует, и притом единственный.

Доказательство.

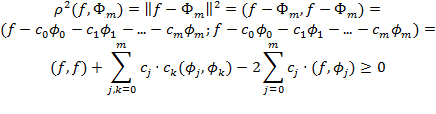
Найдем вектор (с₀,с₁,..., с_m) такой, чтобы квадратичная форма была минимальной. Для этого продифференцируем квадратичную форму сначала по с₁, затем по с₂ и т.д. и полученные выражения приравняем к нулю. Получим систему:

Эта система называется нормальной.

По лемме 1 определитель системы, являющийся определителем Грамма линейно независимой системы функций , не равен нулю. Поэтому система имеет только одно решение (с₀,с₁,..., с_m), в которой квадратичная форма достигает минимума.

 

Определение. В пространстве E_c непрерывных функций со скалярным произведением имеет вид: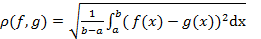

а в пространстве E_n+1 функций, определенных на дискретном множестве 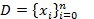со скалярным произведением 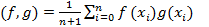среднеквадратичное расстояние задается формулой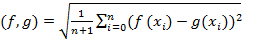

Замечание. Близость двух непрерывных функций в смысле среднеквадратичного уклонения, не гарантирует малость их максимального уклонения друг от друга.

Пример.gº0,

y

x

a

b

n

f

Среднеквадратичные приближения алгебраическими многочленами.

В качестве системы функций берутся степени x: . Система этих функций линейно независима в E[a,b] при любом m.

Пример. Построить на отрезке [0,1] многочлен наилучшего среднеквадратичного приближения Ф₁(x)=c₀+c₁x для функции f(x)= .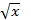

Решение. , , , ,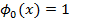

, , .

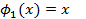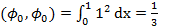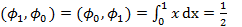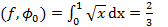Нормальная система уравнений:

 

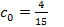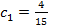, и Ф₁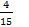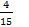(x)= + x.

Среднеквадратическое уклонение Ф₁ от f равно

.

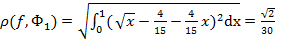На отр [a,b]

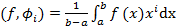, i=0,1,..., m.

 

 

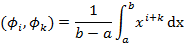
Для дискретного варианта разобрали раньше

Число точек должно быть в 1,5 -2 раза больше.

 

Применение ортогональных многочленов.

Решение нормальной системы уравнений находится наиболее просто, если система функций является ортогональной. Тогда матрица коэффициентов становиться диагональной и 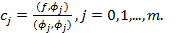Они называются коэффициентами Фурье по ортогональной системе .

 

 

Пример. Построить на отр [0,1]

системы и их свойства.

Пусть H-гильбертово пространство со скалярным произведением и нормой.

Примеры гильбертовых пространств.

1. H-пространство комплекснозначных функций, определенных на [a,b] с ограниченным интервалом .

Скалярное произведение задается равенством , p>0 почти всюду на [a,b].

(Функции считаются равными, если отличаются друг от друга на множестве меры 0).

2. H-евклидово пространство